Ubuntu网络环境配置

在安装完vm和Ubuntu之后，我使用了Iifconfig，我的目的是查看该虚拟机是否网络连通了，是否可以使用网络，很遗憾的是，没有。下面进行网络环境配置的总结。

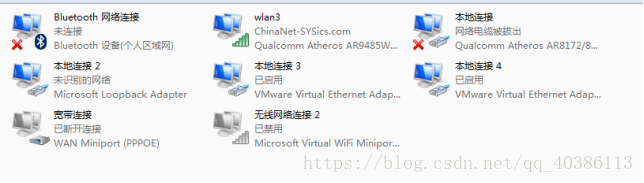
首先你需要做的是打开你windows上的网络和共享中心，点击更改网络适配器，在这里面你可以查看到你现在电脑的网络使用情况。

我跳的第一个坑就是在这，你在配置网络环境的时候需要在windows的cmd中输入ipconfig查看网络，这么多网络（上面显示的是我已经警用或未启用的了），我到底需要的是哪一个，这也是一个小白linux使用者面临的第一个问题，配置ip什么的，我要找的ip是哪个？

在这里，我把除了正在使用的网络之外的禁用了，而且给正在使用的网络，右键单击修改了一个名字，这样我使用cmd中的ipconfig查看，就很直观的知道了我需要的信息。

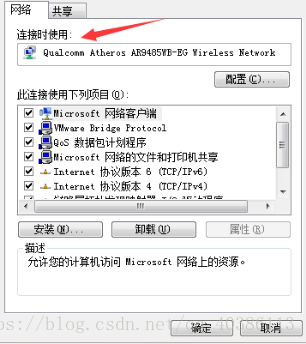
知道了我正在使用的网络，查看正在使用的网络属性，你就会看到下面这张图

这个里面的连接时使用，看好了，就这个名字里面的内容就是你在Ubuntu里面配置网络时候需要使用的第一个东西。

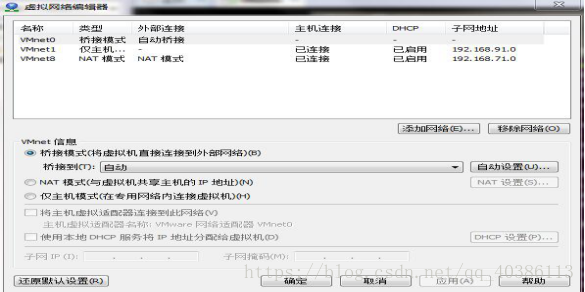
虚拟网络编辑器，在这之前我一直有个疑问就是虚拟机网络信息是怎么来的。上面那个连接时使用里面的内容就是虚拟网络编辑器中桥接模式中的选择内容，这下，很多疑问就能想同了，和外部网络（windows）连接的第一步。

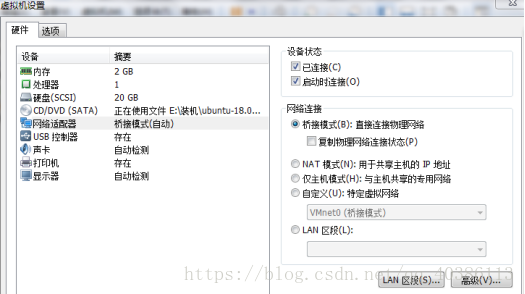
在桥接模式中选择对应的网络信息之后，进入Ubuntu的设置信息中，在网络适配器中选择桥接模式。至于为什么选择桥接模式，不是没有道理，这里到底选择什么模式，我现在的建议就是，只要能连上网络就好，这里的模式最终的目的就是为了连接网络，不管桥接还是NAT，只要选择了能连接网络就好，这个配置真的也没有十分肯定的选择，有的文章中说选择桥接，有的说NAT，是桥接还是NAT，还跟在虚拟网络编辑器中的选择有关。不要太在意这个，目的就是连上网，连上网就不要纠结。为什么在这不负责任的这么说，因为我发现这个东西很神奇，不同的镜像文件它就是会出不同的问题，Ubuntu18和Ubuntu16、Ubuntu14的体验完全不一样，如果你换一个Centos，你又会发现它又要变。

不过上面这种情况也是可控的，在windows那边查清网络信息，在虚拟网络编辑器中选择对应信息，在选择网络适配器的时候就选择桥接，一般不会有问题。记得在查文章的时候，看到过这么一句话，选择NAT模式可以，那么选择桥接模式也可以。个人猜想，这个模式选择可能有一个域大小的不同，时间问题，在这就没去具体查看。

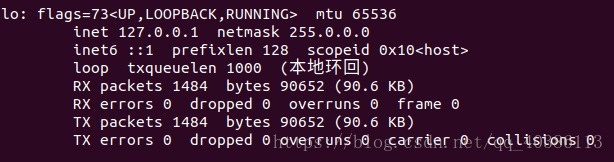
为什么一定要完成上面的设置呢？原因就是你在安装了之后，在终端输入ifconfig之后，打多少时候你会发现，实际情况是下面这样的：

我要说的是，这样还是好的，我遇到过不是这样的情况，它会提醒你什么也没有，就连这个本地环回也没有。

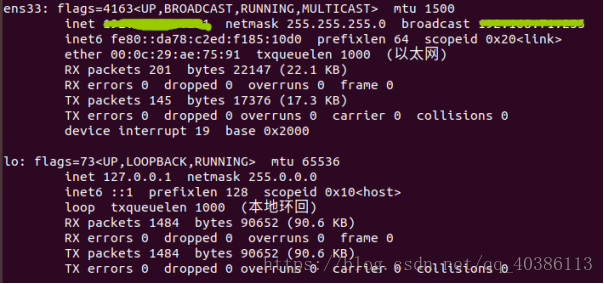
当输入ifconfig，出现上面这种情况，说白了就是网络没连接，没通。所以你要通过上面说的方式先通网络。这是为什么呢？我先上一张通网络的图

说明一下，我使用的是Ubuntu18，为什么说明这个，注意最上面最前面的ens33，有没有很陌生又很熟悉，没错，这里不应是eth0吗，这个要注意，这个坑，很容易跳，我已经上上下下好几次了。

在Centos（没用过Centos7）中，包括Ubuntu中的以前版本中都是eth0，但是就在Ubuntu18中，它是ens33了，记住这个，有用。

上面是连通网络后输入ifconfig后看到的信息，你可以看到ip，网关等信息。这时候，你可以使用ping去看看，你能不能ping通baidu.com，能不能ping通220.181.57.217，关键还有能不能ping通你的windows中的ip，能不能ping通你上面显示的ip。也能很直观的看出来，如果有问题，是不会显示你的ip，网关等信息的。如果能，那么恭喜你，如果不能，只能说没办法，继续向下吧。首先查看一下你上面的虚拟网络编辑器，设置等有没有问题，毕竟这样能解决问题是最好的。有时候你有必要输入reboot（重启）试一下。一般来说是没有问题的。