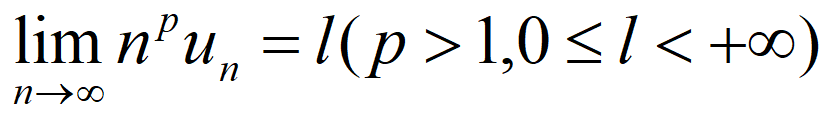定理
Suppose f ( x ) f(x) f(x) is continuous, positive and decreasing on [ 1 , ∞ ] \left[ 1,\infty \right] [1,∞]. If a n = f ( n ) a_n=f(n) an=f(n) for all n = 1 , 2 , . . . n=1,2,... n=1,2,..., then
∑ n = 1 ∞ a n i s c o n v e r g e n t . ⟺ ∫ 1 + ∞ f ( x ) d x i s c o n v e r g e n t \sum_{n=1}^{\infty}{a_n\ is\ convergent.\ \Longleftrightarrow \ \int_1^{+\infty}{f\left( x \right) dx\ is\ convergent}} n=1∑∞an is convergent. ⟺ ∫1+∞f(x)dx is convergent
假设 f ( x ) f(x) f(x) 在区间 [ 1 , ∞ ] \left[ 1,\infty \right] [1,∞]上是递减的正项连续函数. 如果对于所有 n = 1 , 2 , . . . n=1,2,... n=1,2,...都有 a n = f ( n ) a_n=f(n) an=f(n) ,则
∑ n = 1 ∞ a n 收 敛 . ⟺ ∫ 1 + ∞ f ( x ) d x 收 敛 \sum_{n=1}^{\infty}{a_n\ 收敛.\ \Longleftrightarrow \ \int_1^{+\infty}{f\left( x \right) dx\ 收敛}} n=1∑∞an 收敛. ⟺ ∫1+∞f(x)dx 收敛
证明
如图所示为 y = f ( x ) y=f(x) y=f(x)的图像
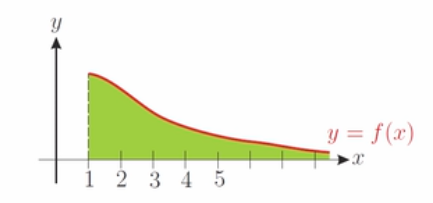
函数 f ( x ) f(x) f(x)在这个区域的反常积分,即 ∫ 1 + ∞ f ( x ) d x \int_1^{+\infty}{f\left( x \right) dx} ∫1+∞f(x)dx,就是绿色区域部分。
使用下黎曼和(lower Riemann sum),如图所示
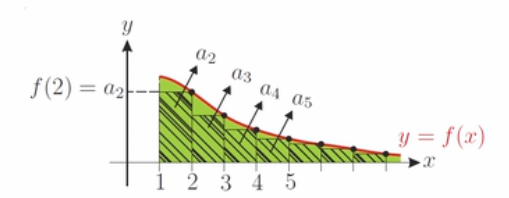
易得出
∑ n = 2 ∞ a n ≤ ∫ 1 + ∞ f ( x ) d x \sum_{n=2}^{\infty}{a_n}\leq \int_1^{+\infty}{f\left( x \right) dx} n=2∑∞an≤∫1+∞f(x)dx
使用上黎曼和(upper Riemann sum),如图所示
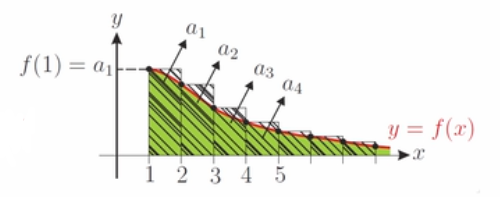
易得出
∫ 1 + ∞ f ( x ) d x ≤ ∑ n = 1 ∞ a n \int_1^{+\infty}{f\left( x \right) dx}\leq \sum_{n=1}^{\infty}{a_n} ∫1+∞f(x)dx≤n=1∑∞an
终上所述
∑ n = 2 ∞ a n ≤ ∫ 1 + ∞ f ( x ) d x ≤ ∑ n = 1 ∞ a n \sum_{n=2}^{\infty}{a_n}\leq \int_1^{+\infty}{f\left( x \right) dx}\leq \sum_{n=1}^{\infty}{a_n} n=2∑∞an≤∫1+∞f(x)dx≤n=1∑∞an
根据比较审敛法
若级数 ∑ n = 1 ∞ a n 收敛,则反常积分 ∫ 1 + ∞ f ( x ) d x 收敛 若反常积分 ∫ 1 + ∞ f ( x ) d x 收敛,则级数 ∑ n = 1 ∞ a n 收敛 \text{若级数\ }\sum_{n=1}^{\infty}{a_n}\ \text{收敛,则反常积分\ }\int_1^{+\infty}{f\left( x \right) dx}\ \text{收敛} \\ \text{若反常积分\,\,}\int_1^{+\infty}{f\left( x \right) dx}\,\,\text{收敛,则级数\,\,}\sum_{n=1}^{\infty}{a_n}\,\,\text{收敛} 若级数 n=1∑∞an 收敛,则反常积分 ∫1+∞f(x)dx 收敛若反常积分∫1+∞f(x)dx收敛,则级数n=1∑∞an收敛
p级数敛散性
由积分审敛法可得
∑ n = 1 ∞ 1 n p 与 ∫ 1 + ∞ 1 x p d x 同敛散 \sum_{n=1}^{\infty}{\frac{1}{n^p}}\ \text{与\ }\int_1^{+\infty}{\frac{1}{x^p}dx}\ \text{同敛散} n=1∑∞np1 与 ∫1+∞xp1dx 同敛散
(1) 0 < p < 1 0<p<1 0<p<1时
∫ 1 + ∞ 1 x p d x = x − p + 1 − p + 1 ∣ 1 + ∞ = lim x → + ∞ ( x − p + 1 − p + 1 ) − 1 − p + 1 \int_1^{+\infty}{\frac{1}{x^p}dx}=\left. \frac{x^{-p+1}}{-p+1} \right|_{1}^{+\infty}=\underset{x\rightarrow +\infty}{\lim}\left( \frac{x^{-p+1}}{-p+1} \right) -\frac{1}{-p+1} ∫1+∞xp1dx=−p+1x−p+1∣∣∣∣1+∞=x→+∞lim(−p+1x−p+1)−−p+11
∵ lim x → + ∞ ( x − p + 1 − p + 1 ) = + ∞ ∴ ∫ 1 + ∞ 1 x p d x 发散 \because \underset{x\rightarrow +\infty}{\lim}\left( \frac{x^{-p+1}}{-p+1} \right) =+\infty \ \ \therefore \int_1^{+\infty}{\frac{1}{x^p}dx}\ \text{发散} ∵x→+∞lim(−p+1x−p+1)=+∞ ∴∫1+∞xp1dx 发散
(2) p = 1 p=1 p=1时
∫ 1 + ∞ 1 x d x = ln x ∣ 1 + ∞ 发散 \int_1^{+\infty}{\frac{1}{x}dx}=\ln x\mid_{1}^{+\infty}\ \text{发散} ∫1+∞x1dx=lnx∣1+∞ 发散
(3) p > 1 p>1 p>1时
∫ 1 + ∞ 1 x p d x = x − p + 1 − p + 1 ∣ 1 + ∞ = lim x → + ∞ ( x − p + 1 − p + 1 ) − 1 − p + 1 \int_1^{+\infty}{\frac{1}{x^p}dx}=\left. \frac{x^{-p+1}}{-p+1} \right|_{1}^{+\infty}=\underset{x\rightarrow +\infty}{\lim}\left( \frac{x^{-p+1}}{-p+1} \right) -\frac{1}{-p+1} ∫1+∞xp1dx=−p+1x−p+1∣∣∣∣1+∞=x→+∞lim(−p+1x−p+1)−−p+11
∵ lim x → + ∞ ( x − p + 1 − p + 1 ) = 0 ∴ ∫ 1 + ∞ 1 x p d x 收敛 \because \underset{x\rightarrow +\infty}{\lim}\left( \frac{x^{-p+1}}{-p+1} \right) =0\ \ \therefore \int_1^{+\infty}{\frac{1}{x^p}dx}\ \text{收敛} ∵x→+∞lim(−p+1x−p+1)=0 ∴∫1+∞xp1dx 收敛
终上所述
当 0 < p ≤ 1 时,级数 ∑ n = 1 ∞ 1 n p 发散,当 p > 1 时,级数 ∑ n = 1 ∞ 1 n p 收敛 \text{当}0<p\leq 1\text{时,级数}\sum_{n=1}^{\infty}{\frac{1}{n^p}}\text{发散,当}p>1\text{时,级数}\sum_{n=1}^{\infty}{\frac{1}{n^p}}\text{收敛} 当0<p≤1时,级数n=1∑∞np1发散,当p>1时,级数n=1∑∞np1收敛