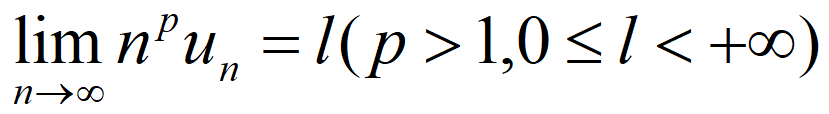常数项级数的收敛法

article/2025/9/26 14:08:29

问题： 大多数级数，很难用定义来研究其敛散性

在这里插入图片描述

一、正项级数及其收敛法

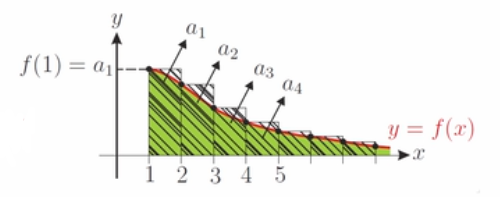
1.1、正项级数（每项非负，部分和数列单调递增）

在这里插入图片描述

1.2、正级数收敛的充要条件： 部分和数列有上界

在这里插入图片描述

1.2.1、推论： 正项级数部分和无上界，则发散

在这里插入图片描述

1.3、比较审敛法

在这里插入图片描述

1.3.1、p级数的敛散性

在这里插入图片描述

例
在这里插入图片描述

1.3.2、p级数与正项等比级数 的对比

在这里插入图片描述

1.3.2.1、例1

在这里插入图片描述

1.3.3、比较审敛法的推论

在这里插入图片描述

1.3.4、比较审敛法的极限形式

在这里插入图片描述

1.5、比值审敛法（达朗贝尔d’Alembert审敛法）

在这里插入图片描述

1.5.1、注意：与p级数进行比较的级数，不能使用比值审敛法

在这里插入图片描述

1.6、根值审敛法（柯西判别法）

在这里插入图片描述
例
在这里插入图片描述

1.7、极限审敛法

在这里插入图片描述

1.8、习题

在这里插入图片描述

二、交错级数及其审敛法

2.1、交错级数

在这里插入图片描述

2.2、莱布尼茨定理

在这里插入图片描述

三、绝对收敛与条件收敛

3.1、定义

在这里插入图片描述

3.2、定理


http://chatgpt.dhexx.cn/article/eFhoZnXu.shtml

相关文章

正项级数收敛性判别方法

正项级数收敛性判别方法

比值判别法 设 Σ n 1 ∞ a n \Sigma _{n1} ^{\infty} a_n Σn1∞​an​为正项级数&#xff0c;且 l i m n − > ∞ a n 1 a n q lim_{n->\infty} {a_{n1}\over a_n}q limn−>∞​an​an1​​q,则有 当 0 < q < 1 0<q<1 0<q<1时&#xff0c;级…
阅读更多...
【高数】级数性质说明、找同阶通项判敛散性、几何级数p级数记忆法、常用例子、审敛法

【高数】级数性质说明、找同阶通项判敛散性、几何级数p级数记忆法、常用例子、审敛法

目录 一、级数性质相关 1. 判敛散性的一个简易方法 2. 几何级数记忆法 3. p级数记忆法 二、常用例子 三、审敛法 四、小结 一、级数性质相关 1. 判敛散性的一个简易方法 针对课本上的级数性质中的某条进一步说明&#xff1a; 级数的数列中的各项同乘一个非零常数&…
阅读更多...
无穷级数 | 等价无穷小（Talor展开）判敛法 交错级数不能用通项等价关系审敛

无穷级数 | 等价无穷小（Talor展开）判敛法 交错级数不能用通项等价关系审敛

一、引例 我们知道&#xff0c;对于正项级数可以利用所谓的通项等价关系进行审敛&#xff0c;即 废话不多说&#xff0c;看例题 &#xff1a; 二、经错标零 例题你觉得简单&#xff1f;下面这坑你必踩~ 经典的错误&#xff0c;标准的零分~ 关注A选项~ 你的做法&#xff1a; 应…
阅读更多...
正项级数的积分审敛法，p级数的敛散性

正项级数的积分审敛法，p级数的敛散性

定理 Suppose f ( x ) f(x) f(x) is continuous, positive and decreasing on [ 1 , ∞ ] \left[ 1,\infty \right] [1,∞]. If a n f ( n ) a_nf(n) an​f(n) for all n 1 , 2 , . . . n1,2,... n1,2,..., then ∑ n 1 ∞ a n i s c o n v e r g e n t . ⟺ ∫ 1 ∞…
阅读更多...
积分审敛法

积分审敛法

若级数An对应函数单调&#xff0c;则该级数敛散性与反常积分敛散性相同
阅读更多...
正项级数及其审敛法

正项级数及其审敛法

一般的常数项级数&#xff0c;各项可以为正数负数或零&#xff0c;我们把只有正数和零的级数称为正项级数。 定理1&#xff1a;正项级数收敛的充要条件是他的部分和数列{sn}有界 snu1u2...un 定理2&#xff1a;若un之和与vn之和都是正项级数&#xff0c;对于任意n&#xff0c;u…
阅读更多...
交错级数及其审敛法

交错级数及其审敛法

称为交错级数 判断下列级数的敛散性 例 1 解:,满足条件1。 满足条件2&#xff0c;所以 收敛。 例 2 所以 都在第一象限&#xff0c;一正一负&#xff0c;所以是交错级数 因为 所以发散 例3 通过求导判断级数的单调性 当x>e时&#xff0c;单调递减 即当时&#xff0…
阅读更多...
第三讲 正项级数的比较审敛法

第三讲 正项级数的比较审敛法

一&#xff0c;用比较审敛法的原因 对于大多数级数&#xff0c;很难得到部分和的表达式&#xff0c;因此很难用定义来研究其敛散性比较审敛法不能用于非正项级数 二&#xff0c;正项级数 定义&#xff1a;&#xff0c;其中部分和为单调递增数列收敛的充要条件&#xff1a;有…
阅读更多...
专升本笔记记载-第七章-无穷级数

专升本笔记记载-第七章-无穷级数

无穷级数 无穷级数概念 例题&解法 例题&解法 (附带结论要背会) 无穷级数定义 倒数第二行记错了, 应该是limit的结果不等于0则发散. 例题1&解法 例题组&解法 三个重要级数 (q级数, p级数, 交错p级数) 常数项级数审敛法 审敛法几乎用在错误选项. 正确选项不用审…
阅读更多...
高数_第6章无穷级数__正项级数的性质_比值_比较_根值_极限审敛法

高数_第6章无穷级数__正项级数的性质_比值_比较_根值_极限审敛法

正项级数要判断敛散性&#xff0c;可以通过以下方法 1. 比较判别法 核心思想&#xff1a; 大的级数收敛&#xff0c; 小的级数也收敛, 小的级数发散&#xff0c; 大的级数也发散。 看一个例题 再看一个例题&#xff1a; 2. 比值审敛法&#xff0c; 也称为达朗贝尔审敛法。 以…
阅读更多...
第四讲 比值、根值和积分审敛法

第四讲 比值、根值和积分审敛法

一&#xff0c;正项级数的比值审敛法 设是正项级数&#xff0c;且&#xff0c;若&#xff0c;则收敛若&#xff0c;则发散若或不存在&#xff0c;则无法判断敛散性例题&#xff0c;如图&#xff1a; 二&#xff0c;正项级数的根值审敛法 设是正项级数&#xff0c;且&#xf…
阅读更多...
java中字符的统计方法

java中字符的统计方法

阅读更多...
java 代码统计工具

java 代码统计工具

java 代码统计工具 项目上线要统计一下所有代码的行数&#xff0c;公司给了个工具&#xff0c;结果用着用着就卡掉卡死&#xff0c;索性自己写了一个&#xff0c;项目不是很大&#xff0c;没用到多线程等技术。下面直接贴代码&#xff1a; import java.io.*; import java.util.…
阅读更多...
JAVA统计图

JAVA统计图

直接看效果&#xff1a; //饼图var echartB;//柱状图var echartZ;var countInfo1"countInfo1";$(function(){GainStatisticsData();});$(window).resize(function () {if(echartZ!undefined){echartZ.resize();}if(echartB!undefined){echartB.resize();}if(echartL…
阅读更多...
SPSS统计描述分析

SPSS统计描述分析

3.1频数分析 频数分布分析主要通过频数分布表、条图和直方图&#xff0c;以及集中趋势和离散趋势的各种统计量&#xff0c;描述数据的分布特征。 例如&#xff0c;要对数据文件做描述性统计分析&#xff0c;并绘制直方图&#xff0c;操作如下&#xff1a; &#xff08;1&…
阅读更多...
精确统计代码量（Java实现）

精确统计代码量（Java实现）

大家面试的时候有没有被问到过这样一个问题&#xff1a; 你的代码量是多少&#xff1f; WHAT&#xff1f;&#xff1f;&#xff1f;代码量&#xff1f;&#xff1f;&#xff1f;我怎么知道&#xff0c;难 道要我去数吗&#xff1f; 下面有简便方法实现&#xff1a; 方法一&…
阅读更多...
描述统计 | 学习笔记 (全)

描述统计 | 学习笔记 (全)

一.导论 统计学是通过收集&#xff0c;整理&#xff0c;分析&#xff0c;描述数据等手段&#xff0c;以达到推断所测对象的本质&#xff0c;甚至预测对象未来的一门综合性科学。其目的是探索数据的内在数量规律性&#xff0c;以达到对客观事物的科学认识 统计的本业是消化数据…
阅读更多...
统计输入的个数（Java）

统计输入的个数（Java）

使用到循环结构中的while循环 public class demo {public static void main(String[] args) {//统计字符的个数//程序要读入一个正整数&#xff0c;然后输出这个整数的位数&#xff1f;//输入&#xff1a;352&#xff0c;输出&#xff1a;3.System.out.println("请输入三位…
阅读更多...
JAVA性能统计项目

JAVA性能统计项目

一、项目背景&#xff1a; 我们希望设计开发一个小的框架&#xff0c;能够获取接口调用的各种统计信息&#xff0c;比如&#xff0c;响应时间的最大值&#xff08;max&#xff09;、最小值&#xff08;min&#xff09;、平均值&#xff08;avg&#xff09;、百分位值&#xff0…
阅读更多...
java中文章的阅读数统计

java中文章的阅读数统计

java中文章的阅读数统计 1.直接操作数据库进行增加操作存在问题 存在问题:每次请求都要update数据库,如果访问量大了之后,数据库存在操作压力,此时怎么办? 解决方法:1.提高数据库性能(横向/纵向拓展)2.使用缓存方式减轻数据压力 推荐使用缓存方式:优点:操作快捷,可以减轻数据…
阅读更多...
推荐文章

Copyright @ 2022~2023