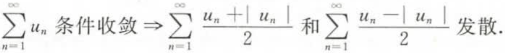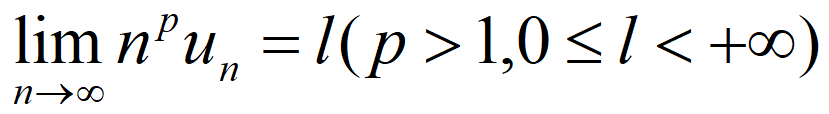目录
- 前言
- 往期文章
- 常数项级数的审敛法
- 一、正项级数及其审敛法
- 定义:正项级数
- 定理1
- 定理2(比较审敛法)
- 推论
- 定理3 (比较审敛法的极限形式)
- 定理4(比值审敛法,达朗贝尔判别法)
- 定理5(比值审敛法,柯西判别法)
- 定理6(极限审敛法)
- 二、交错级数及其审敛法
- 定义:交错级数
- 定理7(莱布尼茨定理)
- 三、绝对收敛与条件收敛
- 定义
- 定理8
- 结语

前言
Hello!小伙伴!
非常感谢您阅读海轰的文章,倘若文中有错误的地方,欢迎您指出~
自我介绍 ଘ(੭ˊᵕˋ)੭
昵称:海轰
标签:程序猿|C++选手|学生
简介:因C语言结识编程,随后转入计算机专业,有幸拿过一些国奖、省奖…已保研。目前正在学习C++/Linux/Python
学习经验:扎实基础 + 多做笔记 + 多敲代码 + 多思考 + 学好英语!
机器学习小白阶段
文章仅作为自己的学习笔记 用于知识体系建立以及复习
知其然 知其所以然!
往期文章
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(1):集合与映射
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(2):线性空间定义及其性质
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(3):线性空间的基与坐标
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(4):基变换与坐标变换
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(5):线性子空间
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(6):子空间的交与和
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(7):欧氏空间
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(8):标准正交基与Gram-Schmidt过程
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(9):正交补与投影定理
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(10):线性变换定义
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(11):线性变换的矩阵表示
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(12):相似形理论
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(13):Hamliton-Cayley定理、最小多项式
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(14):向量范数及其性质
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(15):矩阵的范数
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(16):向量和矩阵的极限
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(17):函数矩阵的微分和积分
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(18):方阵的幂级数
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(19):不定积分(补充知识)
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(20):方阵函数
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(21):常用方阵函数的一些性质
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(22):方阵函数在微分方程组中的应用
【机器学习|数学基础】Mathematics for Machine Learning系列之矩阵理论(23):常数项级数的概念和性质(补充知识)
常数项级数的审敛法
一、正项级数及其审敛法
定义:正项级数
一般的常数项级数,各项可以为正数、负数或零
各项都是正数或零的级数,称为正项级数
定理1
正项级数 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un收敛的充分必要条件是:它的部分和数列 s n s_n sn有界
定理2(比较审敛法)
设 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un和 ∑ n = 1 ∞ v n \sum_{n=1}^{\infty}v_n ∑n=1∞vn都是正项级数,且 u n ≤ v n ( n = 1 , 2 , . . . ) u_n\leq v_n(n=1,2,...) un≤vn(n=1,2,...)
-
若级数 ∑ n = 1 ∞ v n \sum_{n=1}^{\infty}v_n ∑n=1∞vn收敛,则级数 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un收敛
-
反之,若 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un发散,则 ∑ n = 1 ∞ v n \sum_{n=1}^{\infty}v_n ∑n=1∞vn发散
推论
如果级数 ∑ n = 1 ∞ v n \sum_{n=1}^{\infty}v_n ∑n=1∞vn收敛,且存在正整数 N N N,使当 n ≥ N n\geq N n≥N时,有
u n ≤ k v n ( k > 0 ) u_n \leq k v_n(k > 0) un≤kvn(k>0)
成立,那么级数 ∑ n = 1 ∞ u n \sum_{n = 1}^{\infty}u_n ∑n=1∞un收敛
如果级数 ∑ n = 1 ∞ v n \sum_{n=1}^{\infty}v_n ∑n=1∞vn发散,且当 n ≥ N n\geq N n≥N时,有
u n ≥ k v n ( k > 0 ) u_n \geq k v_n(k > 0) un≥kvn(k>0)
成立,那么级数 ∑ n = 1 ∞ u n \sum_{n = 1}^{\infty}u_n ∑n=1∞un收敛发散
定理3 (比较审敛法的极限形式)
设 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un和 ∑ n = 1 ∞ v n \sum_{n=1}^{\infty}v_n ∑n=1∞vn都是正项级数
(1) 如果 lim n → ∞ u n v n = l ( 0 ≤ l < + ∞ ) \lim_{n \rightarrow\infty}\frac{u_n}{v_n}=l(0\leq l< +\infty) limn→∞vnun=l(0≤l<+∞),且级数 ∑ n = 1 ∞ v n \sum_{n=1}^{\infty}v_n ∑n=1∞vn收敛,那么级数 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un收敛
(2)如果 lim n → ∞ u n v n = l ( l > 0 ) \lim_{n \rightarrow\infty}\frac{u_n}{v_n}=l(l > 0) limn→∞vnun=l(l>0)或 lim n → ∞ u n v n = + ∞ \lim_{n \rightarrow\infty}\frac{u_n}{v_n}=+\infty limn→∞vnun=+∞,且级数 ∑ n = 1 ∞ v n \sum_{n=1}^{\infty}v_n ∑n=1∞vn发散,那么级数 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un发散

定理4(比值审敛法,达朗贝尔判别法)
设 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un为正项级数,如果
lim n → ∞ u n + 1 u n = ρ \lim_{n\rightarrow \infty}\frac{u_{n+1}}{u_n}=\rho n→∞limunun+1=ρ
那么
-
ρ < 1 \rho< 1 ρ<1时,级数收敛
-
ρ > 1 \rho>1 ρ>1或 lim n → ∞ u n + 1 u n = ∞ \lim_{n\rightarrow \infty}\frac{u_{n+1}}{u_n}=\infty limn→∞unun+1=∞时级数发散
-
ρ = 1 \rho = 1 ρ=1时,级数可能收敛,也可能发散
定理5(比值审敛法,柯西判别法)
设 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un为正项级数,如果
lim n → ∞ u n n = ρ \lim_{n\rightarrow\infty}\sqrt[n]{u_n}=\rho n→∞limnun=ρ
那么当
- ρ < 1 \rho < 1 ρ<1时级数收敛
- ρ > 1 \rho > 1 ρ>1或 lim n → ∞ u n n = + ∞ \lim_{n\rightarrow\infty}\sqrt[n]{u_n}=+\infty limn→∞nun=+∞时级数发散
- ρ = 1 \rho = 1 ρ=1时级数可能收敛,可能发散
定理6(极限审敛法)
(1)如果 lim n → ∞ n u n = l > 0 \lim_{n\rightarrow\infty} nu_n = l > 0 limn→∞nun=l>0或 lim n → ∞ n u n = + ∞ \lim_{n\rightarrow\infty} nu_n =+\infty limn→∞nun=+∞,那么级数 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un发散
(2)如果 p > 1 p > 1 p>1,而 lim n → ∞ n p u n = l ( 0 ≤ l < + ∞ ) \lim_{n\rightarrow\infty}n^p u_n = l(0 \leq l < +\infty) limn→∞npun=l(0≤l<+∞),那么级数 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un收敛
二、交错级数及其审敛法
定义:交错级数
各项都是交错的,例如
u 1 − u 2 + u 3 − u 4 + . . . . . u_1 - u_2 + u_3 - u_4 + ..... u1−u2+u3−u4+.....
或
− u 1 + u 2 − u 3 + u 4 − . . . . . -u_1 + u_2 - u_3 + u_4 - ..... −u1+u2−u3+u4−.....
定理7(莱布尼茨定理)
如果交错级数 ∑ n = 1 ∞ ( − 1 ) n − 1 u n \sum_{n=1}^{\infty}(-1)^{n-1}u_n ∑n=1∞(−1)n−1un满足条件
(1) u n ≥ u n + 1 ( n = 1 , 2 , 3 , . . . . ) u_n \geq u_{n+1}\quad(n = 1, 2, 3,....) un≥un+1(n=1,2,3,....)
(2) lim n → ∞ u n = 0 \lim_{n\rightarrow\infty}u_n = 0 limn→∞un=0
三、绝对收敛与条件收敛
定义
一般的级数
u 1 + u 2 + . . . . + u n + . . . u_1 + u_2 + .... +u_n +... u1+u2+....+un+...
其各项为任意实数
如果级数 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un各项的绝对值所构成的正项级数 ∑ n = 1 ∞ ∣ u n ∣ \sum_{n=1}^{\infty}|u_n| ∑n=1∞∣un∣收敛
那么称级数 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un绝对收敛
如果级数 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un收敛,而级数 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un发散
则称级数 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un条件收敛
定理8
如果级数 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un绝对收敛,那么级数 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑n=1∞un必定收敛
结语
说明:
- 参考于 课本《高等数学》
- 配合书中概念讲解 结合了自己的一些理解及思考
文章仅作为学习笔记,记录从0到1的一个过程
希望对您有一点点帮助,如有错误欢迎小伙伴指正