一,简介

通过搭建环境,可以在任何地方(公司,家里,地铁...)使用客户端登录,来访问公司的其他机器,但不影响非公司网络的访问(百度,微博,淘宝...)

二,搭建前的准备

注意,以下开始,使用的ip都是假的,根据自己服务器ip自行更换

1,服务器A,centos7系统,内网ip 192.168.0.1

2,服务器B,centos7系统,内网ip 192.168.0.2

2,openconnect客户端

三,开始搭建

服务器A

下面👇🏻的命令,依次执行,服务器A就配置好了,建议慢慢看都做了些什么

# 禁用防火墙
systemctl stop firewalld
systemctl disable firewalld# 开启ipv4 转发
echo "1" > /proc/sys/net/ipv4/ip_forward
# 加载ip_gre模块
modprobe ip_gre# 建立到服务器B的gre隧道,可以通过 ip tunnel list 或 ip route,查看是否添加成功,建立gre隧道
ip tunnel add gre mode gre remote 192.168.0.2 local 192.168.0.1 
# 给gre隧道远端接口添加ip地址
ip addr add 10.10.10.2/24 dev gre
# 启用gre隧道接口
ip link set gre up# 新增虚拟路由表HK（默认所有接口走路由表main，不新增虚拟表,无法走gre 路由）
# vi /etc/iproute2/rt_tables # 新增    100     hk 条目 保存退出
echo "100     hk" >> /etc/iproute2/rt_tables
# 刷新路由表
ip route flush table hk# 当客户端通过拨号连接时,服务端会给客户端分配一个10.10.9.0 - 10.10.9.255的随机地址,这个地址可以在/etc/ocserv/ocserv.conf中修改
# 把来自10.10.9.0/24的数据包,通过hk路由表发送出去,优先级100,可以执行 ip rule list 查看是否添加成功
ip rule add from 10.10.9.0/24 table hk prio 100# 默认路由发送到 10.10.10.2，也就是服务器B的gre隧道ip地址,可以执行 ip route show table hk 查看是否成功
ip route add default via 10.10.10.2 table hk
# 至此 定义新表后 所有来自Cisco的流量默认都会走向服务器B# 安装 epel-release 源
yum -y install epel-release
# 安装 ocserv
yum -y install ocserv# 新建一个目录，用来存放SSL证书相关文件,然后进入到这个目录内
mkdir ~/ssl && cd ~/ssl# 新建一个证书模板,写入
echo "cn = 'h3c'
organization = 'h3c.IM'
serial = 1
expiration_days = 9999
ca
signing_key
cert_signing_key
crl_signing_key" > ca.tmpl# 然后生成私钥和CA证书：
certtool --generate-privkey --outfile ca-key.pem
certtool --generate-self-signed --load-privkey ca-key.pem --template ca.tmpl --outfile ca-cert.pem# 接着来生成服务器证书，还是老样子新建一个证书模板：
echo "cn = '你的服务器IP'
organization = 'TEST.IM'
expiration_days = 9999
signing_key
encryption_key
tls_www_server" > server.tmpl# 然后生成私钥和证书：
certtool --generate-privkey --outfile server-key.pem
certtool --generate-certificate --load-privkey server-key.pem --load-ca-certificate ca-cert.pem --load-ca-privkey ca-key.pem --template server.tmpl --outfile server-cert.pem# 然后把证书文件用移动到Ocserv默认的目录下：
cp server-cert.pem /etc/pki/ocserv/public/
cp server-key.pem /etc/pki/ocserv/private/
cp ca-cert.pem /etc/pki/ocserv/cacerts/# 现在编辑ocserv的配置文件
# auth也就是验证方式要改为密码验证
sed -i 's/auth = "pam"/#auth = "pam"/g' /etc/ocserv/ocserv.conf
echo 'auth = "plain[passwd=/etc/ocserv/ocpasswd]"' >> /etc/ocserv/ocserv.conf# 默认的监听端口为443，如果你的服务器上跑着HTTPS的WEB站点，那么443端口肯定是被占用了的，所以如果有需求的话，可以更改下面的值：
# sed -i 's/tcp-port = 443/tcp-port = 8080/g' /etc/ocserv/ocserv.conf 
# sed -i 's/udp-port = 443/udp-port = 8080/g' /etc/ocserv/ocserv.conf# Anyconnect可以限制最大允许连接的设备数量，如有需要可以更改下面这两个值：
# sed -i 's/max-clients = 16/max-clients = 32/g' /etc/ocserv/ocserv.conf
# sed -i 's/max-same-clients = 2/max-same-clients = 6/g' /etc/ocserv/ocserv.conf# 更改服务器证书以及私钥的路径为刚才移动的路径：
sed -i 's~server-cert = /etc/pki/ocserv/public/server.crt~server-cert = /etc/pki/ocserv/public/server-cert.pem~g' /etc/ocserv/ocserv.conf
sed -i 's~server-key = /etc/pki/ocserv/private/server.key~server-key = /etc/pki/ocserv/private/server-key.pem~g' /etc/ocserv/ocserv.conf# 更改CA证书的路径为刚才移动的路径：
sed -i 's~ca-cert = /etc/pki/ocserv/cacerts/ca.crt~ca-cert = /etc/pki/ocserv/cacerts/ca-cert.pem~g' /etc/ocserv/ocserv.conf# 这个意思是下放远端DNS 建议注释掉不要用远端
sed -i 's/dns = 8.8.8.8/#dns = 8.8.8.8/g' /etc/ocserv/ocserv.conf# 设置分配给客户端的私人ip
echo "ipv4-netmask = 255.255.255.0" >> /etc/ocserv/ocserv.conf
echo "ipv4-network = 10.10.9.0/24" >> /etc/ocserv/ocserv.conf
echo "tunnel-all-dns = false" >> /etc/ocserv/ocserv.conf# 设置请求哪些ip,走gre通道,这里设置的ip,才会走<<网络流程图>>上画的流程,可以把公司的服务器ip可以添加在这里
# 192.168.0.1 - 192.168.0.255的数据包,走gre隧道,
echo "route = 192.168.0.0/255.255.255.0" >> /etc/ocserv/ocserv.conf
echo "route = 10.10.10.0/255.255.255.0" >> /etc/ocserv/ocserv.conf# 到8.8.8.8 的数据包,走gre隧道
#echo "route = 8.8.8.8/255.255.255.255" >> /etc/ocserv/ocserv.conf# 创建一个用户,执行下面的命令之后,会让盲输两遍密码
ocpasswd -c /etc/ocserv/ocpasswd lala# 删除一个用户,可以在这 /etc/ocserv/ocpasswd 看有哪些用户
# ocpasswd -c /etc/ocserv/ocpasswd -d lala# 启动ocserv 服务
systemctl start ocserv
systemctl status ocserv

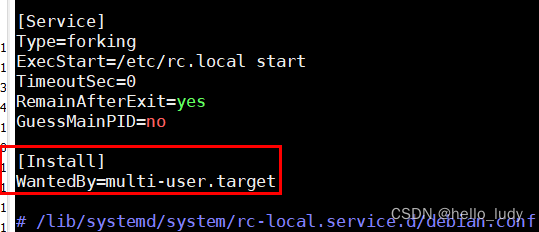
上面的命令,有些是临时生效的,重启后就没了,所以,部分命令要写到 /etc/rc.local,开机时会自动执行,把下面的命令粘贴进去就行

systemctl stop firewalld
systemctl disable firewalld
echo "1" > /proc/sys/net/ipv4/ip_forward
modprobe ip_gre
ip tunnel add gre mode gre remote 192.168.0.2 local 192.168.0.1
ip rule add from 10.10.9.0/24 table hk prio 100
ip route add default via 10.10.10.2 table hk

粘贴完之后,记得执行下面俩命令,要不然没权限

chmod +x /etc/rc.d/rc.localchmod +x /etc/rc.local

至此,服务器A上需要做的事情,全部完成

服务器B

# 禁用防火墙
systemctl stop firewalld
systemctl disable firewalld# 开启ipv4 转发
echo "1" > /proc/sys/net/ipv4/ip_forward# 加载ip_gre模块
modprobe ip_gre# 建立到服务器A的gre隧道,可以通过 ip tunnel list 或 ip route,查看是否添加成功
ip tunnel add gre mode gre remote 192.168.0.1 local 192.168.0.2
# 给gre隧道远端接口添加ip地址
ip addr add 10.10.10.1/24 dev gre
# 启用gre隧道接口
ip link set gre up# 到10.10.9.0/24的数据包,发送到 10.10.10.1 也就是服务器A的gre隧道ip
ip route add 10.10.9.0/24 via 10.10.10.1# 把来自 10.10.9.0/24 网段的数据包,通过eth0网卡发送出去,把10.10.9.0/24 替换成本机的ip,执行 iptables -L -n --line-number -t nat 查看是否成功,
# 可以通过 "iptables -t nat -D POSTROUTING 编号" 删除规则
iptables -t nat -A POSTROUTING -o eth0 -s 10.10.9.0/24 -j MASQUERADE

至此,服务器A和B上要做的事情都已做完,接下来是客户端