目录
一、级数性质相关
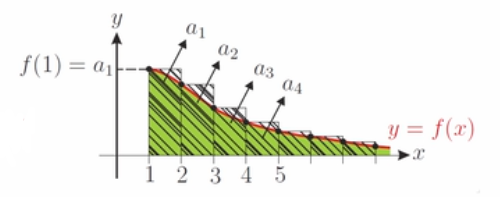
1. 判敛散性的一个简易方法
2. 几何级数记忆法
3. p级数记忆法
二、常用例子
三、审敛法
四、小结
一、级数性质相关
1. 判敛散性的一个简易方法
针对课本上的级数性质中的某条进一步说明:
级数的数列中的各项同乘一个非零常数,不改变级数的敛散性。(即收敛的仍收敛,发散的仍发散。)
注:在需要判断敛散性时,因为不知道往收敛还是发散的方向证明,所以需要找到相对题干级数更为小发散,或大收敛的级数,最差的情况下要找到两个级数!
在用正项级数比较审敛法的极限形式时,本质上是在看,分子分母上的两个级数通项,在n→∞时,谁是更为高阶的无穷小。在高阶低阶的情况下,与比较审敛法并无差异。但是当二者同阶时,也即两级数的极限是非零常数倍的关系,此时由上可知,敛散性相同。
结合上述对级数性质的说明,可以用这样一个简便的方法。即找到与待判级数通项的同阶的通项,用新找到的级数的敛散性判断,则减少了工作量。
2. 几何级数记忆法
几何级数,就是等比级数,可以结合等比数列求和公式来记忆。公比 q ≥ 1 或 q ≤ -1,首先通项的极限就是∞了,该和不存在。而 -1 <q <1,收敛,此时通项极限是0,且可由公式得出极限。
(引自百度百科:https://baike.baidu.com/item/%E5%87%A0%E4%BD%95%E7%BA%A7%E6%95%B0)

3. p级数记忆法
课本上是说,p>0的情况,但事实上,p<0显然是有意义的,且通项的极限是∞,因此是发散的。所以可以简单记忆 p>1,收敛,其余都发散。不过大多数教材及文章中,都将p级数归为正项级数,此时又称 “调和级数 ”,所以只讨论了p>0的情况,具体范围如何取,应视题目而定。
(引自百度百科:https://baike.baidu.com/item/p%E7%BA%A7%E6%95%B0)

二、常用例子
1. 选择题,常用的例子整理(这里省略上下标)。
发散: (因为p级数)
收敛(指它本身收敛,而未必绝对收敛):
2. 一个很厉害很好记的级数:
,与它同敛散的反常积分是
其敛散性与a、b有关:
可以想成因为 x 是比 lnx 大许多的无穷大,所以基本上先由它决定敛散性。所以先看a。
- a>1, 收敛。a<1, 发散。
- a=1,此时看b。
- b>1, 收敛。b<1, 发散。
疑问:级数和反常积分的关系?后面再次复习反常积分时总结。
三、审敛法
在这里放一些总结得比较全的文章,指路链接:
《级数收敛的判别方法(知识汇总)》:https://m.xianjichina.com/news/details_83466.html
《第五讲 交错级数、绝对收敛和条件收敛》:https://blog.csdn.net/qq_23940575/article/details/84610895
《P-达朗贝尔判别法及其应用》:https://www.ixueshu.com/document/7ea4c75acbc0c8e9381c0aab81c124ec.html
可以用比值判别法的,用根值判别法一定可以。反之未必。
,诸如此类带有 C+(-1)^n 的通项,用比值判别法会因为奇偶项而有所不同,比值时而>1,时而<1。但是用根值判别法,便可忽略此项,因为开n次方后分子得1,而分母是2。
四、小结
1. 级数的数列中的各项同乘一个非零常数,不改变级数的敛散性。因此找到与待判级数通项的同阶的通项,二者敛散性相同。
2. 几何级数:-1 <q <1,收敛,其余发散。p级数,p>1,收敛,其余都发散。
3. 常用例子:,
,
,
。
4. 可以用比值判别法的,用根值判别法一定可以。反之未必。