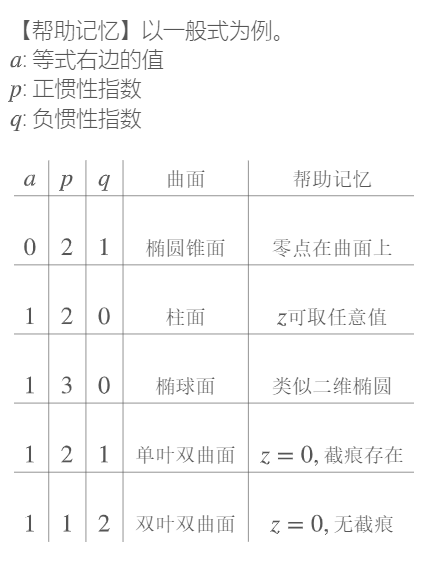
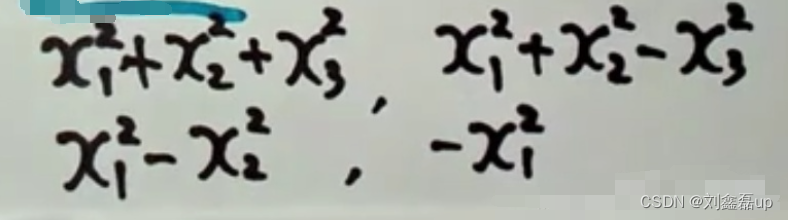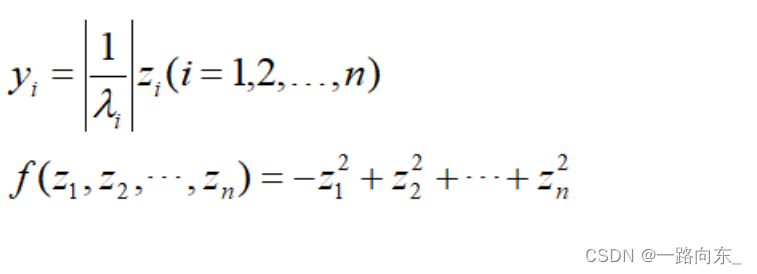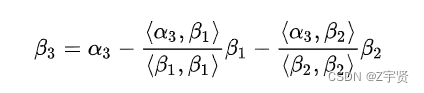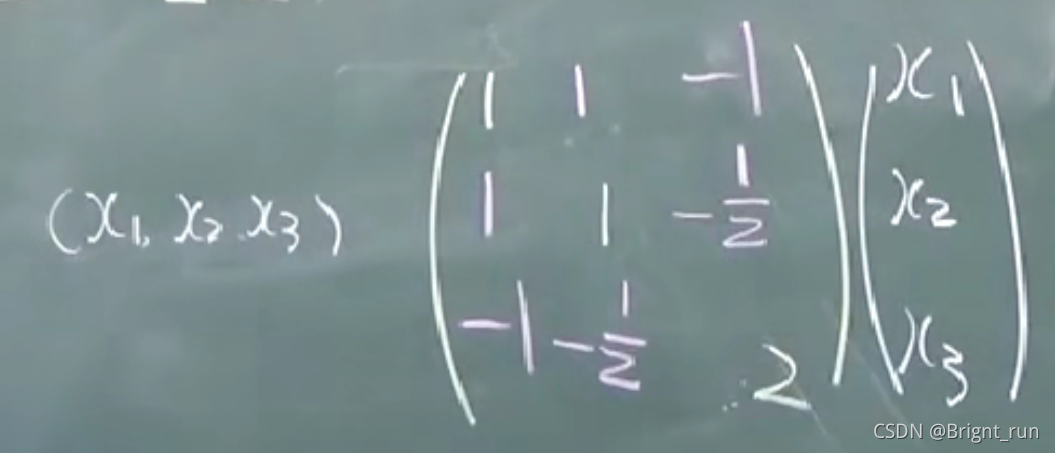二次型:含有n个变量 x 1 , x 2 , . . . x n x_1,x_2,...x_n x1,x2,...xn的二次齐次函数:
f ( x 1 , x 2 , . . . x n ) = a 11 x 1 2 + a 12 x 1 x 2 + a 13 x 1 x 3 + a 14 x 1 x 4 . . . + a 1 n x 1 x n f(x_1,x_2,...x_n)=a_{11}x_1^2+a_{12}x_1x_2+a_{13}x_1x_3+a_{14}x_1x_4...+a_{1n}x_1x_n f(x1,x2,...xn)=a11x12+a12x1x2+a13x1x3+a14x1x4...+a1nx1xn
+ a 21 x 2 x 1 + a 22 x 2 2 + a 23 x 1 x 3 + a 24 x 2 x 4 . . . + a 2 n x 2 x n +a_{21}x_2x_1+a_{22}x_2^2+a_{23}x_1x_3+a_{24}x_2x_4...+a_{2n}x_2x_n +a21x2x1+a22x22+a23x1x3+a24x2x4...+a2nx2xn
…
+ a n 1 x n x 1 + a n 2 x n x 2 + a n 3 x n x 3 + a n 4 x n x 4 . . . + a n n x n 2 +a_{n1}x_nx_1+a_{n2}x_nx_2+a_{n3}x_nx_3+a_{n4}x_nx_4...+a_{nn}x_n^2 +an1xnx1+an2xnx2+an3xnx3+an4xnx4...+annxn2
称为二次型。 二次型可以用矩阵表示记作:
f = X T A X f=X^TAX f=XTAX
其中 X = [ x 1 x 2 . . . x n ] X=\begin{bmatrix} x_1\\ x_2\\ ...\\x_n \end{bmatrix} X=⎣⎢⎢⎡x1x2...xn⎦⎥⎥⎤, A = [ a 11 a 12 . . . a 1 n a 21 a 22 . . . a 2 n . . . a n 1 a n 2 . . . a n n ] A=\begin{bmatrix} a_{11}&a_{12}&...&a_{1n}\\ a_{21}&a_{22}&...&a_{2n}\\ ...\\a_{n1}&a_{n2}&...&a_{nn} \end{bmatrix} A=⎣⎢⎢⎡a11a21...an1a12a22an2.........a1na2nann⎦⎥⎥⎤,可以通过先计算 A X AX AX,再计算 X T A X X^TAX XTAX来证明:
A X = [ a 11 x 1 + a 12 x 2 + . . . + a 1 n x n a 21 x 1 + a 22 x 2 + . . . + a 2 n x n . . . a n 1 x 1 + a n 2 x 2 + . . . + a n n x n ] AX=\begin{bmatrix} a_{11}x_1+a_{12}x_2+...+a_{1n}x_n\\ a_{21}x_1+a_{22}x_2+...+a_{2n}x_n\\ ...\\a_{n1}x_1+a_{n2}x_2+...+a_{nn}x_n \end{bmatrix} AX=⎣⎢⎢⎡a11x1+a12x2+...+a1nxna21x1+a22x2+...+a2nxn...an1x1+an2x2+...+annxn⎦⎥⎥⎤在左乘 X T X^T XT得到原式:
[ x 1 x 2 . . . x n ] [ a 11 x 1 + a 12 x 2 + . . . + a 1 n x n a 21 x 1 + a 22 x 2 + . . . + a 2 n x n . . . a n 1 x 1 + a n 2 x 2 + . . . + a n n x n ] \begin{bmatrix} x_1\\ x_2\\ ...\\x_n \end{bmatrix}\begin{bmatrix} a_{11}x_1+a_{12}x_2+...+a_{1n}x_n\\ a_{21}x_1+a_{22}x_2+...+a_{2n}x_n\\ ...\\a_{n1}x_1+a_{n2}x_2+...+a_{nn}x_n \end{bmatrix} ⎣⎢⎢⎡x1x2...xn⎦⎥⎥⎤⎣⎢⎢⎡a11x1+a12x2+...+a1nxna21x1+a22x2+...+a2nxn...an1x1+an2x2+...+annxn⎦⎥⎥⎤
我们来求一下二次型的导数:
d f ( x 1 , x 2 , . . . x n ) d x 1 = 2 a 11 x 1 + a 12 x 2 + a 13 x 3 + a 14 x 4 . . . + a 1 n x n \frac{df(x_1,x_2,...x_n)}{dx_1}=2a_{11}x_1+a_{12}x_2+a_{13}x_3+a_{14}x_4...+a_{1n}x_n dx1df(x1,x2,...xn)=2a11x1+a12x2+a13x3+a14x4...+a1nxn
+ a 21 x 2 + 0 + 0 + 0... + 0 +a_{21}x_2+0+0+0...+0 +a21x2+0+0+0...+0
…
+ a n 1 x n + 0 + 0 + 0... + 0 +a_{n1}x_n+0+0+0...+0 +an1xn+0+0+0...+0
= 2 a 11 x 1 + ( a 12 + a 21 ) x 2 + ( a 13 + a 31 ) x 3 + ( a 14 + a 41 ) x 4 . . . + ( a 1 n + a n 1 ) x n =2a_{11}x_1+(a_{12}+a_{21})x_2+(a_{13}+a_{31})x_3+(a_{14}+a_{41})x_4...+(a_{1n}+a_{n1})x_n =2a11x1+(a12+a21)x2+(a13+a31)x3+(a14+a41)x4...+(a1n+an1)xn,其余的还有对 x 1 , x 2 . . . x n x_1,x_2...x_n x1,x2...xn的求导。
正定二次型:设二次型 f = X T A X f=X^TAX f=XTAX,如果对任何 X ≠ 0 X\neq0 X̸=0,都有 f ( X ) > 0 f(X)>0 f(X)>0,则称 f f f为正定二次型,并称对称矩阵 A A A是正定的。
由于 A A A是对称矩阵,所以其导数为:
d f ( x 1 , x 2 , . . . x n ) d x 1 = 2 a 11 x 1 + 2 a 12 x 2 + 2 a 13 x 3 + 2 a 14 x 4 . . . + 2 a 1 n x n \frac{df(x_1,x_2,...x_n)}{dx_1}=2a_{11}x_1+2a_{12}x_2+2a_{13}x_3+2a_{14}x_4...+2a_{1n}x_n dx1df(x1,x2,...xn)=2a11x1+2a12x2+2a13x3+2a14x4...+2a1nxn
d f ( x 1 , x 2 , . . . x n ) d x 2 = 2 a 21 x 1 + 2 a 22 x 2 + 2 a 23 x 3 + 2 a 24 x 4 . . . + 2 a 2 n x n \frac{df(x_1,x_2,...x_n)}{dx_2}=2a_{21}x_1+2a_{22}x_2+2a_{23}x_3+2a_{24}x_4...+2a_{2n}x_n dx2df(x1,x2,...xn)=2a21x1+2a22x2+2a23x3+2a24x4...+2a2nxn
. . . . .... ....
所以 ▽ f ( X ) = 2 A X \bigtriangledown f(X)=2AX ▽f(X)=2AX
举个例子:

其对其求导可得矩阵:
▽ f ( X ) = [ 2 x − 4 y − 4 x + z . . . − 6 z + y ] \bigtriangledown f(X)=\begin{bmatrix} 2x-4y\\ -4x+z\\ ...\\-6z+y \end{bmatrix} ▽f(X)=⎣⎢⎢⎡2x−4y−4x+z...−6z+y⎦⎥⎥⎤