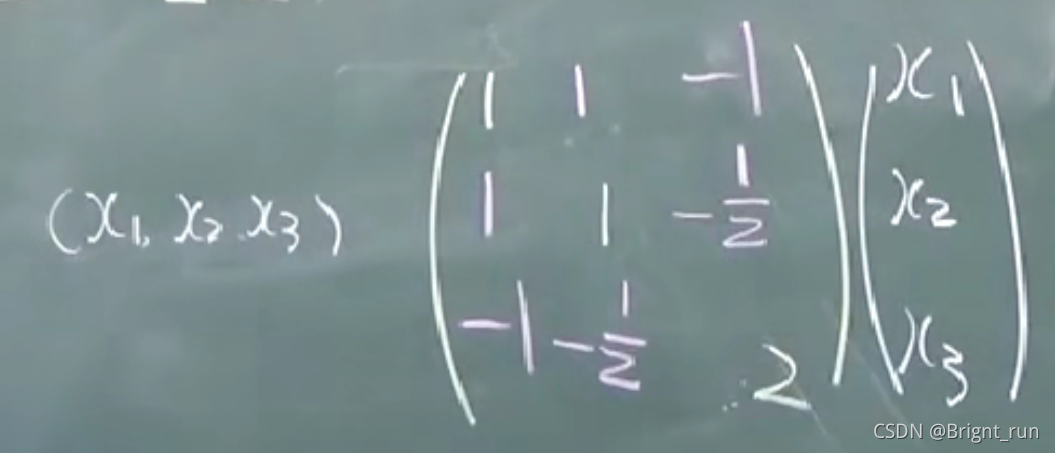在学习二次型的时候没有好好理解概念,导致记住了可以用的结论,但往往遇到题目反应不过来,故这次对二次型进行一个详细剖析。
首先二次型是什么?是一个n元变量的二次齐次多项式,根据二次齐次多项式的定义(所有单项的次数都是2,单项的次数为其所有变数字母指数之和),这也注定了二次型每一个单项不是单个字母的平方,就是两个一次指数字母的乘积。所以别看二次型中变量是x1,x2其实可以变化成x,y,z这样的话可不能辨别不出来。比如f(x,y,z) = xy+yz+zx,这个也是一个二次型,这可不能辨别不出来哦!(所有的二次型都是在实对称矩阵上的。)
但是我们为了方便研究二次型,所以我们规定二次型的矩阵(二次型 = )必须是实对称矩阵,为了更进一步方便研究,就得想办法将其中的两个一次指数的变量删除掉,只留下二次的单个字母,所以就有了我们常说的标准型和规范型。那么通过怎么样的方式来变换成这样的这两种形态呢?可逆线性变换!
任何普通二次型都可以通过配方法(即可逆线性变化的一种方式)化成标准型和规范型。
任何普通二次型都可以通过正交变换化成标准型。
需要注意上述两句话的区别,配方法本质就是可逆线性变化的外在表现形式,而正交变换是将转置和可逆联系起来,以至于将可逆线性变化等同于相似对角化,但是相似对角化不管怎么变化,其特征值都是不变化的,故得出的对角矩阵这个实对称矩阵中间元素不一定是正负1,故得此结论。
在通过这两种基本方法可逆线性变化的过程中,有一个惯性定律,即任何普通的二次型不管经过怎么样不同的可逆线性变化,化成最后怎么不同的标准型和规范型,其最后标准型和规范型中的正项的个数,即正惯性指数,负项个数,即负惯性指数都是不变的。(值得一提的是,如果通过正交矩阵进行可逆线性变化,如果不通过配方法进一步可逆线性变化的话,其最后得出的对角矩阵中特征值是唯一的,即特征值不变,即正负惯性指数不变,矩阵会改变,因为特征值改变位置,矩阵就变化了。而如果是配方法得出的对角矩阵是不唯一的,取决于其可逆矩阵C,而且得出的对角矩阵中间元素往往不是初始二次型矩阵A的特征值,因为C碰巧是正交矩阵的概率太小了,但但是正负惯性指数是唯一的。)
有了上述的两句结论,就有了对于任何实对称矩阵而言,必然存在一个可逆矩阵C使得经过可逆线性变化变成对角矩阵。所以就有了我们在相似里面学到的,实对称矩阵比可相似对角化,因为可逆矩阵C里面存在正交矩阵使得相似对角化。
那上述两种方式的本质是什么呢?——找到时可逆矩阵C。
正交变化法的本质就是沟通了转置和可逆,使得可逆线性变化 = 相似对角化,由于相似对角化能够很轻松的找到可逆正交C(即为A的特征向量组),所以便可将其当做可逆线性变化的C。
使用史密斯正交化的条件?——只要矩阵A的特征向量全部线性无关就好了。
什么是合同?合同是二次型可逆现象变化的副产品,可以用合同表示二次型可逆线性变化的核心,方便研究。合同其实其实就是二次型的可逆线性变化,可逆线性变化会有正负惯性指数相同,那么合同的充要条件也是正负惯性指数不变,如果变化就不是可逆线性变化,那么合同也会不成立的,可以理解为合同为可逆线性变化的代言人。合同的充要条件还有定义法和传递性。
那么接下来就可以讨论一个特殊的二次型,正定二次型。
其定义为:对于任意不为零的n元变量组成的列向量,都有二次型>0,那么这个就是正定二次型,即二次型f(x1,x2.。。)>0的
充要条件:A的特征值都大于0,正惯性指数 = n,A与E合同(即最后可逆线性变化化成规范型之后中间全为1),A的全部顺序主子式都大于0(行列式),存在可逆D,有(这个根据A和E合同变化过来的,其中的D为C的逆)
必要条件:A矩阵中间的aii都是大于0的,同时A的行列式大于0(A的行列式为特征值的乘积,由于特征值全是正的,那么行列式自然是正的,但是反过来不可以,因为偶数个负数特征值行列式也大于0,所以这个是必要条件,而非充要)。
重要结论:

总的来说二次型问题就是一个怎么标准化和规范化的问题,不要感到害怕!
史密斯正交化
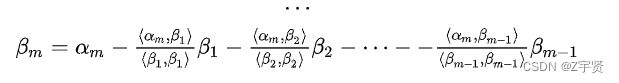
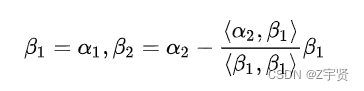
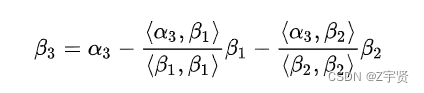
先标后规——标准型中间可以不是正负一,但是规范性的后面全是政正负一。
关于线性变换和基变换的区别:线性变换用的多,是大佬,所以C在前面 X = CY,表示X到Y的线性变化,其实质是元素;基变换用的少,是小弟,所以C在后面 有 Z = MC,表示M到Z的基变换。