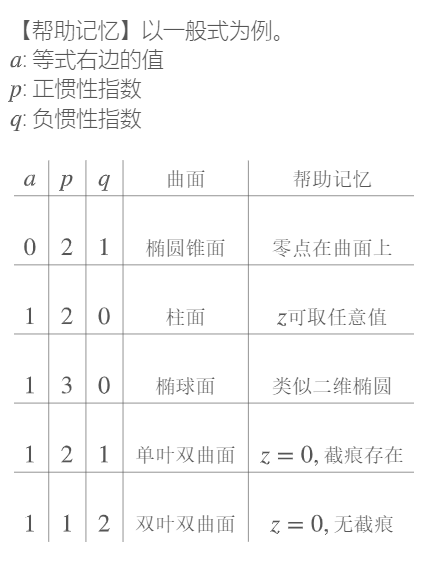
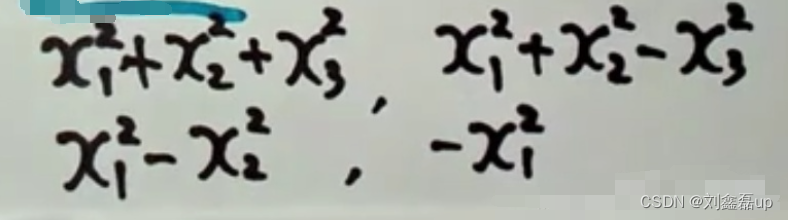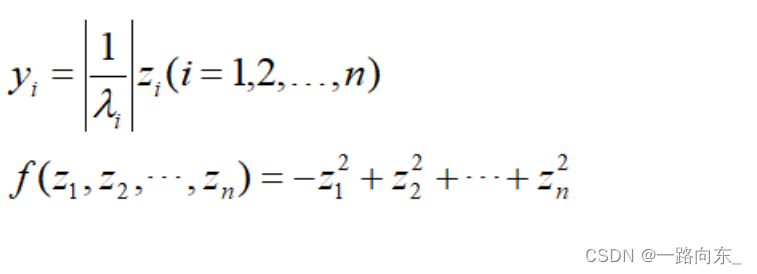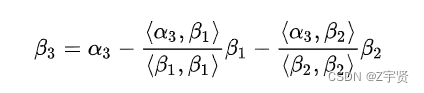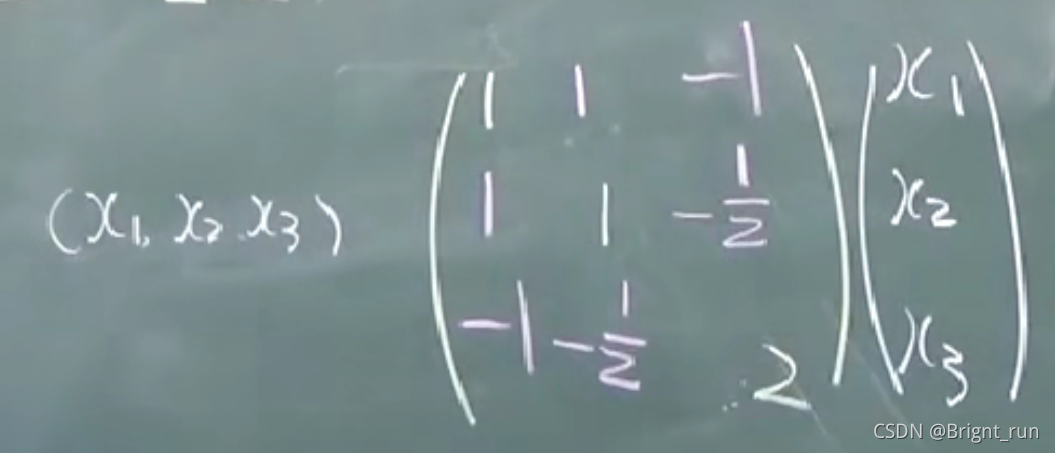二次型的正定

article/2025/10/2 19:16:21

实数二次型的类型

设f(x_{1},x_{2}...x_{n})=X^{T}AX为一个实二次型，若\forall X=\begin{pmatrix} x_{1}\\ x_{2}\\ ...\\ x_{n} \end{pmatrix}\neq 0

自变量x_{1},x_{2}...x_{n}不全为0

若f(x_{1},x_{2}...x_{n})=X^{T}AX> 0恒成立，则称f为一个正定二次型，称A为正定矩阵

若f(x_{1},x_{2}...x_{n})=X^{T}AX\geq 0恒成立，则称f为一个半正定二次型，称A为半正定矩阵

若f(x_{1},x_{2}...x_{n})=X^{T}AX< 0恒成立，则称f为一个负定二次型，称A为负定矩阵

若f(x_{1},x_{2}...x_{n})=X^{T}AX\leq 0恒成立，则称f为一个半负定二次型，称A为半负定矩阵

定理：\begin{vmatrix} a_{11} &a_{12} & a_{13}\\ a_{21}&a_{22} &a_{23} \\ a_{31}&a_{32} & a_{33} \end{vmatrix}

若f=X^{T}AX正定\Leftrightarrow经过一个可逆的线性变换X=CY，得f=Y^{T}BY也正定

如何判断A是否为正定矩阵？

正定矩阵首先是二次型，二次型是对称矩阵，所以首先判断A是否对称阵。

1、根据定义判断

2、根据特征值判断，因为用正交变换得到的标准型，y^{2}前的系数就是特征值，如果特征值全部大于0，那么肯定f大于0

3、顺序主子式法，A的左上角各阶顺序主子式全大于0

例如A=\begin{vmatrix} a_{11} &a_{12} & a_{13}\\ a_{21}&a_{22} &a_{23} \\ a_{31}&a_{32} & a_{33} \end{vmatrix}，那么就是依次求\begin{vmatrix} a_{11} \end{vmatrix}的行列式，\begin{vmatrix} a_{11} &a_{12} \\ a_{21} & a_{22} \end{vmatrix}的行列式，\begin{vmatrix} a_{11} &a_{12} & a_{13}\\ a_{21}&a_{22} &a_{23} \\ a_{31}&a_{32} & a_{33} \end{vmatrix}的行列式是否全部大于0

4、如果A与E合同，则A正定

这个很好判断啊，由2+定理，可得只要A的规范型里，系数都为1，那么A就是正定

5、A的正惯性指数为n，则A正定

正定的必要条件

若f=X^{T}AX为正定，可以推出

1）A的主对角线a_{ii}全部大于0

2）A的行列式大于0

这个由2就可以判断出了


http://chatgpt.dhexx.cn/article/ppZUHcqE.shtml

相关文章

线性代数-二次型及其正定性

线性代数-二次型及其正定性

二次型及其矩阵表示形式 二次型:含有n个变量的二次齐次多项式 二次型矩阵:xTAx,其中A为实对称矩阵 任给一个实二次型,就唯一确定一个实对称矩阵;反之,任给一个实对称矩阵,也可以唯一确认一个实二次型,因此,实二次型与实对称矩阵之间存在一一对应关系,称实对称矩阵A为二次型f的…
阅读更多...
【考研线代】六. 二次型

【考研线代】六. 二次型

文章目录 第六章 二次型6.1 二次型及其标准形6.1.1 概念6.1.2 合同基本性质6.1.3 题型 6.2 正定二次型6.2.1 概念6.2.2 定理 6.3 补充&#xff1a;解题技巧6.3.1 惯性定理的理解6.3.2 矩阵合同的充要条件6.3.3 配方法的坐标变换必须可逆6.3.4 正交变化化标准型 &#xff08;&am…
阅读更多...
线性代数（10）：二次型

线性代数（10）：二次型

一、二次型 &#xff08;1&#xff09;定义 含有 n 个变量 x1&#xff0c;x2&#xff0c;…… &#xff0c;xn 的二次齐次函数称为二次型&#xff1b; 对称矩阵 A 的秩也叫做二次型 f 的秩&#xff1b; &#xff08;2&#xff09; 例&#xff1a; 排列二次型 所对应的矩阵 …
阅读更多...
二次型化标准形的三种方法

二次型化标准形的三种方法

二次型化标准形的三种方法 将二次型化为标准形有利于我们了解二次型的简单形式、二次型的各种参数如正负惯性指数、得到二次型的规范形、对称矩阵合同的简单形等等。另外&#xff0c;化标准形也是解析几何化简二次曲线和二次曲面的需要。 下面&#xff0c;我们以两道题目为例…
阅读更多...
二次型化标准形的五种方法

二次型化标准形的五种方法

文章目录 1. 配方法2. 初等变换法3. 正交变换法4. 偏导数法5. 顺序主子式法 1. 配方法 用配方法化二次型为标准形的关键是消去交叉项&#xff0c;分如下两种情况&#xff1a; 情形1&#xff1a;如果二次型 f ( x 1 , x 2 , x 3 , ⋯ , x n ) {f \left( x\mathop{{}}\nolimits…
阅读更多...
区别：二次型、标准形、规范形

区别：二次型、标准形、规范形

文章目录&#xff1a; 一&#xff1a;二次型 二次型衔接 合同和相似 二&#xff1a;标准形 二次型化为标准形 1.配方法 2.正交变换法 三&#xff1a;规范形 标准形&#xff1a;不唯一规范形&#xff1a;唯一 一&#xff1a;二次型 二次型&#xff1a;对称矩阵 A&#…
阅读更多...
速通二次型、二次型标准型、二次型规范型

速通二次型、二次型标准型、二次型规范型

浅过二次型 理解二次型可以从二次型的多项式入手&#xff1a; 显然&#xff0c;在系数都为实数的情况下&#xff0c;二次型矩阵即为一个实对称矩阵。 取一个代入值的例子就是&#xff1a; 二次型的标准型 OK&#xff0c;再从二次型的标准型的多项式入手&#xff0c;如下&…
阅读更多...
二次型的来龙去脉

二次型的来龙去脉

在学习二次型的时候没有好好理解概念&#xff0c;导致记住了可以用的结论&#xff0c;但往往遇到题目反应不过来&#xff0c;故这次对二次型进行一个详细剖析。 首先二次型是什么&#xff1f;是一个n元变量的二次齐次多项式&#xff0c;根据二次齐次多项式的定义&#xff08;所…
阅读更多...
二次型二次型矩阵

二次型二次型矩阵

二次型 二次型&#xff08;Quadratic form&#xff09;是关于一些变量的二次齐次多项式 二次型矩阵 表达形式跟矩阵的相似雷同&#xff0c;只是换成了转置 规范二次型 二次型化标准型 配方 将含有x1的项集中起来进行配方 非退化线性替换 合同变换 故标准型为 非退化线性…
阅读更多...
线性代数——二次型

线性代数——二次型

一&#xff1a;通过矩阵研究二次方程 二次型的定义&#xff1a; 把含有n个变量的二次齐次函数或方程称为二次型&#xff0c;例如&#xff1a; 二次型可以用矩阵来表示&#xff1a; 可以表示为 更一般的情况&#xff1a; 可以表示为 令&#xff1a;&#xff0c;&#xff0…
阅读更多...
线性代数(六)——二次型

线性代数(六)——二次型

文章目录 前言二次型是什么&#xff1f;二次型的表示合同矩阵与合同二次型正定二次型、正定矩阵二次型的题型 前言 一直对二次型和线性代数的关系不解&#xff0c;导致一系列的知识点因为没有理解而常常忘记。 在这里对二次型进行梳理&#xff0c;希望可以加深对二次型的印象。…
阅读更多...
高等代数---二次型

高等代数---二次型

高等代数—二次型 声明&#xff1a; 本篇文章内容主要对《高等代数》第三版第五章内容的总结&#xff0c;复习 基本概念&#xff1a; 二次型的矩阵&#xff1b;标准形&#xff0c;规范形 二次型及其矩阵表示 从代数的观点看,所谓化标准方程就是用变量的线性替换化简一个二次…
阅读更多...
二次型的意义与应用

二次型的意义与应用

二次型在数学很多分支里都频繁出现,而且在其他学科也到处可见。比如实二次型4c似乎在非常多的应用中都出现过,比如优化、概率图论、统计、机器学习、信号处理等等。那么,二次型在你所学的领域有什么应用呢?।希望大家能列出二次型在自己领域内对应的具体问题,是如何求解的等等…
阅读更多...
二次型矩阵

二次型矩阵

二次型的每一项都是二次的&#xff0c;如果是平方则是平方项&#xff0c;如果是两个不同的变量则为交叉项。二次型如&#xff1a; x 2 x y y 2 x^2xyy^2 x2xyy2。 二次型->矩阵表达式 例&#xff1a; x 1 2 2 x 1 x 2 x 2 2 − x 2 x 3 2 x 3 2 − 2 x 1 x 3 x_1^22x_…
阅读更多...
二次型

二次型

二次型理论起源于解析几何中化二次曲线或 二次曲面方程为标准形问题. 这里首先介绍一些 基本概念&#xff0c;然后讨论如何利用可逆线性变换把一 个二次型化成标准形。 二次曲面 二次型及其标准形的概念 定义 含有n个变量 x 1 , x 2 , . . . , x n x_{1},x_{2},...,x_{n} x1​…
阅读更多...
【线性代数】四、二次型

【线性代数】四、二次型

第四章 二次型 文章目录 第四章 二次型一、二次型定义二、合同变换1.线性变换2.矩阵合同标准型和规范型 3.惯性定理 三、正定二次型 一、二次型定义 如果系数aij全为实数&#xff0c;那么为实二次型。上述二次型展开式可表示用矩阵为 可以看出&#xff0c;二次型矩阵A是一个对…
阅读更多...
二次型（Quadratic Form）

二次型（Quadratic Form）

1.二次型 二次型&#xff08;quadratic form&#xff09;&#xff1a;n个变量的二次多项式称为二次型&#xff0c;即在一个多项式中&#xff0c;未知数的个数为任意多个&#xff0c;但每一项的次数都为2的多项式。 它起源于几何学中二次曲线方程和二次曲面方程化为标准形问题的…
阅读更多...
二次型定义

二次型定义

二次型用矩阵表达式表示 &#xff0c; 1 平方项的系数直接做成主对角元素 2. 交叉项的系数除以2&#xff0c;放到两个对称的相应位置上。 , ,的平方项系数为 1 &#xff0c;1 &#xff0c;2放在对角线上&#xff0c;如下图红色部分&#xff1b; 交叉项部分 &#xff0c…
阅读更多...
如何理解二次型？

如何理解二次型？

通过矩阵来研究二次函数&#xff08;方程&#xff09;&#xff0c;这就是线性代数中二次型的重点。 1 二次函数&#xff08;方程&#xff09;的特点 1.1 二次函数 最简单的一元二次函数就是&#xff1a; 给它增加一次项不会改变形状&#xff1a; 增加常数项就更不用说了&…
阅读更多...
常微分方程-变量分离、变量变换、线性微分方程和常数变易法

常微分方程-变量分离、变量变换、线性微分方程和常数变易法

阅读更多...
推荐文章

Copyright @ 2022~2023