二次型用矩阵表达式表示

，

1 平方项的系数直接做成主对角元素

2. 交叉项的系数除以2，放到两个对称的相应位置上。

,  ,的平方项系数为 1 ，1 ，2放在对角线上，如下图红色部分；

交叉项部分   ， 2/2放在第一行第二例，即第二行第一例；

  将-1/2放在第二行第三列，和第三行第二列；

将-2/2放在第一行第三列，和第三行一第列；

  ，  -2x_{1}x_{3}

记作 ,A就叫二次型的矩阵。

二次型的矩阵一点是对称的。

转置性质：

只有平方项,叫做标准项；

线性替换   X=CY

矩阵A对称则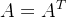

合同：A,B是两个n阶的方阵，如果存 在可逆矩阵C，使得,就叫两个矩阵合同；

1) ;(A和它自己合同)

2)如果,那么;

3) ,；

4)  那么r(A)=r(b)；

5)如果 ，,那么(A对称，那么B也对称)

6）如果 ，如果 A,B可逆，那么；

7） 如果，那么；

---

二次型化标准型(初等变换，正交替换)

任意一个可逆矩阵，都可以表现成一个初等矩阵的乘积

左乘行变换，右乘列变换;

1）对A,E做同样的初等列变换;

2）只对A做初等行变换;

通过例子来说明

解 :第一列*-1加到第二列

马上做行变换，第一行*-1加到第二行上

第一列*-1，加到第 三行上

马上做行变换，第一行*-1加到第三行上

第二列*-1，加到第 三例上

马上做行变换，第二行*-1，加到第三行

上三行，则是

下三行

有定性

有定性的判别：

1）正定二次型经过线性替换，仍是正定。

正定，