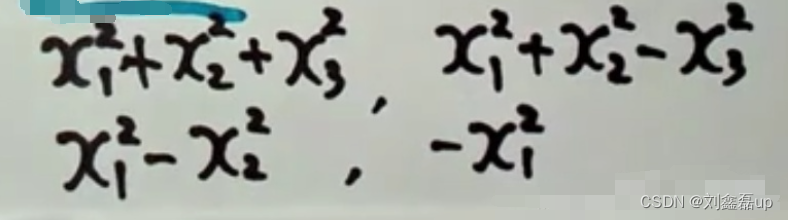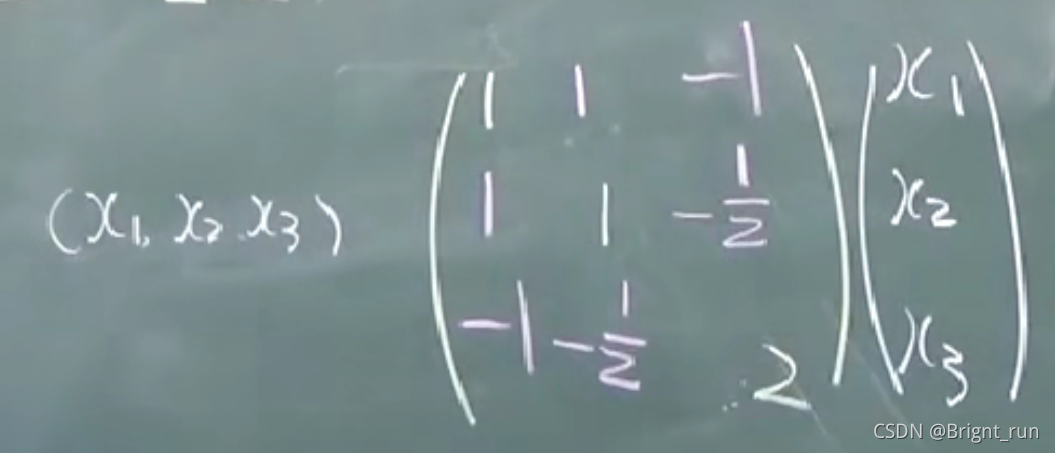二次型化标准形的三种方法
将二次型化为标准形有利于我们了解二次型的简单形式、二次型的各种参数如正负惯性指数、得到二次型的规范形、对称矩阵合同的简单形等等。另外,化标准形也是解析几何化简二次曲线和二次曲面的需要。
下面,我们以两道题目为例说明计算二次型的标准形的三种方法:
- 配方法
- 合同变换法
- 特征值法
第一题
例1 计算二次型 X T A X = x 1 2 + 5 x 2 2 + 5 x 3 2 + 2 x 1 x 2 − 4 x 1 x 3 \displaystyle X^TAX=x_1^2+5x_2^2+5x_3^2+2x_1x_2-4x_1x_3 XTAX=x12+5x22+5x32+2x1x2−4x1x3的标准形.
方法一:配方法
配方法的要领是:第一次将所有含有 x 1 x_1 x1的项集中到一起,进行配方,从而消掉含有 x 1 x_1 x1的交叉项,第二次将含有 x 2 x_2 x2的项集中到一起进行配方……直到去掉所有的交叉项.
解:将含有 x 1 \displaystyle x_1 x1的项集中起来进行配方:
X T A X = x 1 2 + 2 x 1 ( x 2 − 2 x 3 ) + 5 x 2 2 + 5 x 3 2 X^TAX=x_1^2+2x_1(x_2-2x_3)+5x_2^2+5x_3^2 XTAX=x12+2x1(x2−2x3)+5x22+5x32
= ( x 1 + x 2 − 2 x 3 ) 2 − ( x 2 − 2 x 3 ) 2 + 5 x 2 2 + 5 x 3 2 =(x_1+x_2-2x_3)^2-(x_2-2x_3)^2+5x_2^2+5x_3^2 =(x1+x2−2x3)2−(x2−2x3)2+5x22+5x32
= ( x 1 + x 2 − 2 x 3 ) 2 + 4 x 2 2 + x 3 2 + 4 x 2 x 3 =(x_1+x_2-2x_3)^2+4x_2^2+x_3^2+4x_2x_3 =(x1+x2−2x3)2+4x22+x32+4x2x3
= ( x 1 + x 2 − 2 x 3 ) 2 + ( 2 x 2 + x 3 ) 2 =(x_1+x_2-2x_3)^2+(2x_2+x_3)^2 =(x1+x2−2x3)2+(2x2+x3)2
= y 1 2 + y 2 2 , =y_1^2+y_2^2, =y12+y22,
其中,非退化线性替换为:
{ x 1 + x 2 − 2 x 3 = y 1 2 x 2 + x 3 = y 2 x 3 = y 3 , \begin{cases} x_1+x_2-2x_3&=&y_1\\ \quad \quad \quad 2x_2+x_3&=&y_2\\\quad \quad \quad \quad \quad \quad x_3&=&y_3\end{cases}, ⎩⎪⎨⎪⎧x1+x2−2x32x2+x3x3===y1y2y3,
即,
{ x 1 = y 1 − 1 2 y 2 + 5 2 y 3 x 2 = 1 2 y 2 − 1 2 y 3 x 3 = y 3 □ \begin{cases}x_1&=&y_1-\frac{1}{2}y_2+\frac{5}{2}y_3\\x_2&=& \frac{1}{2}y_2-\frac{1}{2}y_3\\ x_3&=&y_3\end{cases}\quad\quad\square ⎩⎪⎨⎪⎧x1x2x3===y1−21y2+25y321y2−21y3y3□
方法二:合同变换法
解:
[ 1 1 − 2 1 5 0 − 2 0 5 1 0 0 0 1 0 0 0 1 ] → − r 1 + r 2 [ 1 1 − 2 0 4 2 − 2 0 5 1 0 0 0 1 0 0 0 1 ] \begin{bmatrix}1&1&-2\\1&5&0\\-2&0&5\\1&0&0\\0&1&0\\0&0&1\end{bmatrix}\xrightarrow{-r_1+r_2}\begin{bmatrix}1&1&-2\\0&4&2\\-2&0&5\\1&0&0\\0&1&0\\0&0&1\end{bmatrix} ⎣⎢⎢⎢⎢⎢⎢⎡11−2100150010−205001⎦⎥⎥⎥⎥⎥⎥⎤−r1+r2⎣⎢⎢⎢⎢⎢⎢⎡10−2100140010−225001⎦⎥⎥⎥⎥⎥⎥⎤
→ − c 1 + c 2 [ 1 0 − 2 0 4 2 − 2 2 5 1 − 1 0 0 1 0 0 0 1 ] → 2 r 1 + r 3 [ 1 0 − 2 0 4 2 0 2 1 1 − 1 0 0 1 0 0 0 1 ] \xrightarrow{-c_1+c_2}\begin{bmatrix}1&0&-2\\0&4&2\\-2&2&5\\1&-1&0\\0&1&0\\0&0&1\end{bmatrix}\xrightarrow{2r_1+r_3}\begin{bmatrix}1&0&-2\\0&4&2\\0&2&1\\1&-1&0\\0&1&0\\0&0&1\end{bmatrix} −c1+c2⎣⎢⎢⎢⎢⎢⎢⎡10−2100042−110−225001⎦⎥⎥⎥⎥⎥⎥⎤2r1+r3⎣⎢⎢⎢⎢⎢⎢⎡100100042−110−221001⎦⎥⎥⎥⎥⎥⎥⎤
→ 2 c 1 + c 3 [ 1 0 0 0 4 2 0 2 1 1 − 1 2 0 1 0 0 0 1 ] → − 1 2 r 2 + r 3 [ 1 0 0 0 4 2 0 0 0 1 − 1 2 0 1 0 0 0 1 ] \xrightarrow{2c_1+c_3}\begin{bmatrix}1&0&0\\0&4&2\\0&2&1\\1&-1&2\\0&1&0\\0&0&1\end{bmatrix}\xrightarrow{-\frac{1}{2}r_2+r_3}\begin{bmatrix}1&0&0\\0&4&2\\0&0&0\\1&-1&2\\0&1&0\\0&0&1\end{bmatrix} 2c1+c3⎣⎢⎢⎢⎢⎢⎢⎡100100042−110021201⎦⎥⎥⎥⎥⎥⎥⎤−21r2+r3⎣⎢⎢⎢⎢⎢⎢⎡100100040−110020201⎦⎥⎥⎥⎥⎥⎥⎤
→ − 1 2 c 2 + c 3 [ 1 0 0 0 4 0 0 0 0 1 − 1 5 2 0 1 − 1 2 0 0 1 ] \xrightarrow{-\frac{1}{2}c_2+c_3}\begin{bmatrix}1&0&0\\0&4&0\\0&0&0\\1&-1&\frac{5}{2}\\0&1&-\frac{1}{2}\\0&0&1\end{bmatrix} −21c2+c3⎣⎢⎢⎢⎢⎢⎢⎡100100040−11000025−211⎦⎥⎥⎥⎥⎥⎥⎤
所以,标准形为,
X T A X = y 1 2 + 4 y 2 2 . X^TAX=y_1^2+4y_2^2. XTAX=y12+4y22.
非退化线性替换矩阵为,
C = [ 1 − 1 5 2 0 1 − 1 2 0 0 1 ] . □ C=\begin{bmatrix}1&-1&\frac{5}{2}\\0&1&-\frac{1}{2}\\0&0&1\end{bmatrix}.\quad\square C=⎣⎡100−11025−211⎦⎤.□
方法三:特征值法
解:令
A = [ 1 1 − 2 1 5 0 − 2 0 5 ] . A=\begin{bmatrix}1&1&-2\\1&5&0\\-2&0&5\end{bmatrix}. A=⎣⎡11−2150−205⎦⎤.
由矩阵的特征多项式
∣ λ E − A ∣ = ∣ λ − 1 − 1 2 − 1 λ − 5 0 2 0 λ − 5 ∣ |\lambda E-A|=\begin{vmatrix}\lambda-1&-1&2\\-1&\lambda-5&0\\2&0&\lambda-5\end{vmatrix} ∣λE−A∣=∣∣∣∣∣∣λ−1−12−1λ−5020λ−5∣∣∣∣∣∣
= 2 r 2 + r 3 ∣ λ − 1 − 1 2 − 1 λ − 5 0 0 2 ( λ − 5 ) λ − 5 ∣ \overset{2r_2+r_3}{=}\begin{vmatrix}\lambda-1&-1&2\\-1&\lambda-5&0\\0&2(\lambda-5)&\lambda-5\end{vmatrix} =2r2+r3∣∣∣∣∣∣λ−1−10−1λ−52(λ−5)20λ−5∣∣∣∣∣∣
= − 2 c 3 + c 2 ∣ λ − 1 − 5 2 − 1 λ − 5 0 0 0 λ − 5 ∣ \overset{-2c_3+c_2}{=}\begin{vmatrix}\lambda-1&-5&2\\-1&\lambda-5&0\\0&0&\lambda-5\end{vmatrix} =−2c3+c2∣∣∣∣∣∣λ−1−10−5λ−5020λ−5∣∣∣∣∣∣
按照第三行展开得,
= ( λ − 5 ) ( λ 2 − 6 λ ) =(\lambda-5)(\lambda^2-6\lambda) =(λ−5)(λ2−6λ)
得到 A \displaystyle A A的特征值为0,5,6.
此时,得到二次型 X T A X X^TAX XTAX的标准形为,
X T A X = 5 y 1 2 + 6 y 2 2 . □ X^TAX=5y_1^2+6y_2^2. \quad\quad \square XTAX=5y12+6y22.□
注:(1)由于二次型的标准形不唯一,所以三种方法得到的结果都不一样。
(2)由于只要求标准形,所以第三种方法所使用的正交变换我们省去不求了,到时专门就“使用正交变换化二次型为标准形”写一篇文章介绍。

第二题
例2 计算二次型 X T A X = − 4 x 1 x 2 + 2 x 1 x 3 + 2 x 2 x 3 X^TAX=-4x_1x_2+2x_1x_3+2x_2x_3 XTAX=−4x1x2+2x1x3+2x2x3的标准形.
由于这道题目没有平方项,所以在使用配方法和合同变换法的时候需要先处理一下,以便化为例1的情况进行求解。特征值法与例1相同,所以不再赘述。
简要解答:
方法一:配方法
分析:为了得到一个平方项,可以将 x 1 x_1 x1设为两数之和,将 x 2 x_2 x2设为这两数之差.
解: 作非退化线性替换,
{ x 1 = y 1 + y 2 x 2 = y 1 − y 2 x 3 = y 3 , \begin{cases}x_1=y_1+y_2\\x_2=y_1-y_2\\x_3=y_3\end{cases}, ⎩⎪⎨⎪⎧x1=y1+y2x2=y1−y2x3=y3,
X T A X = − 4 y 1 2 + 4 y 2 2 + 4 y 1 y 3 , X^TAX=-4y_1^2+4y_2^2+4y_1y_3, XTAX=−4y12+4y22+4y1y3,
下面的步骤与例1同.
方法二:合同变换法
分析:为了将左上角变出一个非零元,可以考虑将第二行(或者第三行)加到第一行,同时将第二列(或者第三列)加到第一列.
解:
[ 0 − 2 1 − 2 0 1 1 1 0 1 0 0 0 1 0 0 0 1 ] → r 3 + r 1 [ 1 − 1 1 − 2 0 1 1 1 0 1 0 0 0 1 0 0 0 1 ] \begin{bmatrix}0&-2&1\\-2&0&1\\1&1&0\\1&0&0\\0&1&0\\0&0&1\end{bmatrix}\xrightarrow{r_3+r_1}\begin{bmatrix}1&-1&1\\-2&0&1\\1&1&0\\1&0&0\\0&1&0\\0&0&1\end{bmatrix} ⎣⎢⎢⎢⎢⎢⎢⎡0−21100−201010110001⎦⎥⎥⎥⎥⎥⎥⎤r3+r1⎣⎢⎢⎢⎢⎢⎢⎡1−21100−101010110001⎦⎥⎥⎥⎥⎥⎥⎤
→ c 3 + c 1 [ 2 − 1 1 − 1 0 1 1 1 0 1 0 0 0 1 0 1 0 1 ] \xrightarrow{c_3+c_1}\begin{bmatrix}2&-1&1\\-1&0&1\\1&1&0\\1&0&0\\0&1&0\\1&0&1\end{bmatrix} c3+c1⎣⎢⎢⎢⎢⎢⎢⎡2−11101−101010110001⎦⎥⎥⎥⎥⎥⎥⎤
下面的步骤与例1同.
欢迎扫描下图中的二维码关注微信公众号:大哉数学之为用

如果您觉得本文对您有帮助,欢迎赞赏!您的支持是作者继续下去的动力!