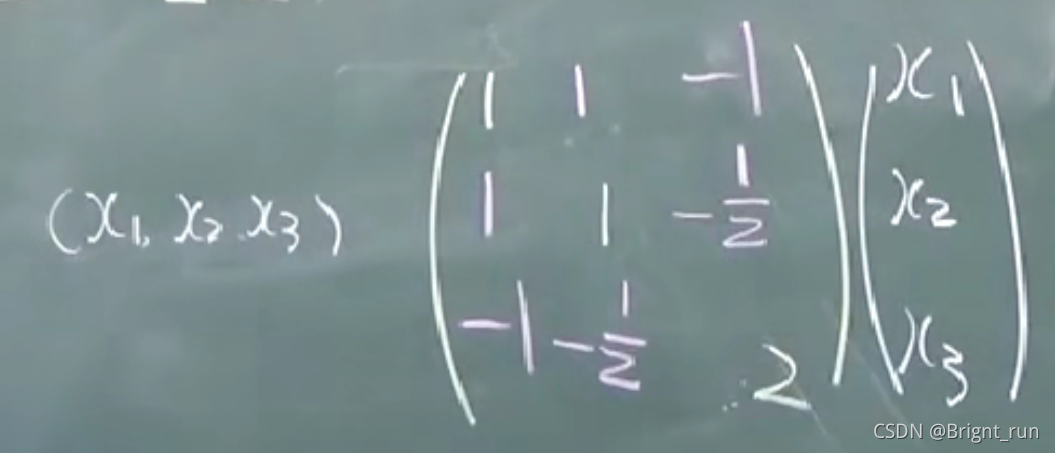高等代数—二次型
声明: 本篇文章内容主要对《高等代数》第三版第五章内容的总结,复习
基本概念: 二次型的矩阵;标准形,规范形
二次型及其矩阵表示
从代数的观点看,所谓化标准方程就是用变量的线性替换化简一个二次齐次多项式使它只含有平方项。
线性替换把二次型变成二次型;研究二次型在非退化的线性替换下的变化情况就是本章的主要目的。


注意:
1.二次型的矩阵都是对称的。
2.经过一个非退化的线性替换,二次型还是变成二次型。
3.经过线性替换合并之后的矩阵任然是对称的。
4.经过非退化的线性替换,新二次型的矩阵与原二次型的矩阵是合同的.
5.在变换二次型时,我们总是要求所作的先行替换是非退化的。(需要再品一下)

标准型
定理1: 数域P上任意一个二次型都可以经过非退化的线性替换变成平方和的形式
证明:本定理分为三种情况来证明,对角线上有非零元素,对角线上全为0但第一行有非零元素,第一行和对角线都是0;
定理2: 在数域P上,任意一个对称矩阵都合同于一对角矩阵.
也就是说,对于任意一个对称矩阵A都可以找到可逆矩阵C 。 使CTAC
注: 该章节主要地内容就是运用这两个定理求解一些实际问题,所以本节课的例题还是很有代表意义的,也是一个重要的考点。详见P219
唯一性
合同的矩阵有相同的秩,也就是说,经过非退化线性替换之后,二次型矩阵的秩是不变的。标准形的矩阵是对角矩阵,而对角矩阵的秩就等于它对角线上不为零的元素的个数。因此,在一个二次型的标准形中,系数不为零的平方项的个数是唯一确定的,与所作的非退化线性替换无关,二次型矩阵的秩有时就称为二次型的秩。
在一般的数域内,二次型的标准形不是唯一的,而与所作的非退化线性替换有关。
定理3 任意一个复系数的二次型,经过一适当的非退化线性替换可以变成规范形,且规范形是唯一的。
定理3换个说法就是,任一复数的对称矩阵合同于一个形式为

定理4: 任意一个实数域上的二次型,经过一适当的非退化线性替换可以变成规范形,且规范形是唯一的。这个定理也被称为惯性定理。(这个定理的证明可以在品一下,没有看的太明白。)

实二次型的标准形中系数为正的平方项的个数是唯一确定的,它等于正惯性指数,而系数为负的平方项的个数就等于负惯性指数。

正定二次型

非退化实线性替换保持正定性不变。

定义5: 实对称矩阵A称为正定的,如果二次型XTAX 正定。
推论:
1.一个实对称矩阵是正定的当且仅当它与单位矩阵合同。
2.正定矩阵的行列式大于零。





链接: 更多高等代数内容点击此处.
参考书籍:《高等代数》第三版 王萼芳 石生明 修订 高等教育出版社