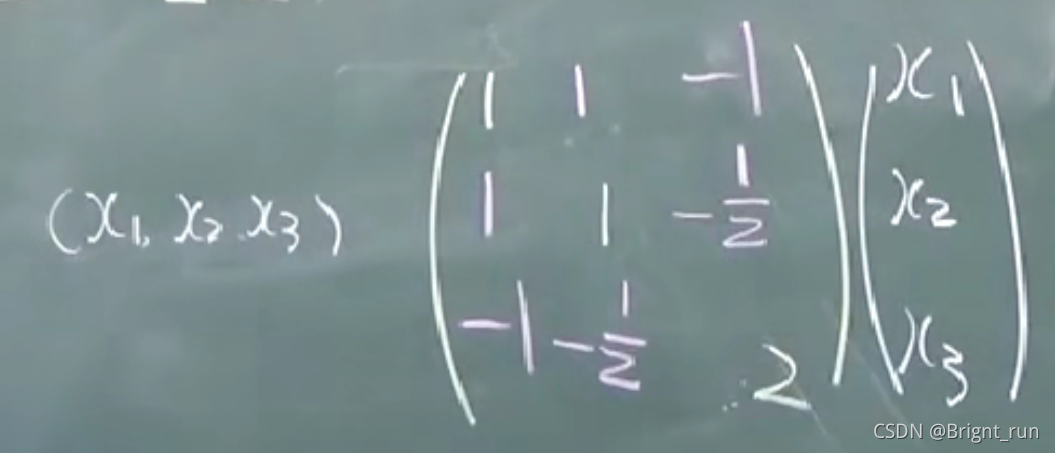线性代数——二次型

一：通过矩阵研究二次方程

二次型的定义：

把含有n个变量的二次齐次函数或方程称为二次型，例如：

$f(x_{1},x_{2},...,x_{n})=a_{11}x_{1}^{2}+a_{22}x_{2}^{2}+...+a_{nn}x_{n}^{2}+2a_{12}x_{1}x_{2}+2a_{13}x_{1}x_{3}+...+2a_{n-1}x_{n-1}x_{n}$

二次型可以用矩阵来表示：

$x^{2}+y^{2}-2xy=1$ 可以表示为 $\begin{bmatrix} x & y \end{bmatrix}\begin{bmatrix} 1 & -1\\ -1 & 1 \end{bmatrix}\begin{bmatrix} x\\y \end{bmatrix}=1$

更一般的情况：

$ax^{2}+2bxy+cy^{2}=1$ 可以表示为 $\begin{bmatrix} x & y \end{bmatrix}\begin{bmatrix} a & b\\ b & c \end{bmatrix}\begin{bmatrix} x\\y \end{bmatrix}=1$

令： $X=\begin{bmatrix} x\\y \end{bmatrix}$ ， $A=\begin{bmatrix} a & b\\ b & c \end{bmatrix}$ ，则上式表示为 $X^{T}AX$ ，这就是我们常见的二次型表示方式。

在《Linear Algebra and Its Applications》中译本《线性代数及其应用》中，二次型的定义如下：

在向量计算中常遇到的 $X^{T}X$ ，求向量元素的平方和，这类平方和及其更一般形式称为二次型。

$R^{n}$ 上的一个二次型是定义在 $R^{n}$ 上的函数，其在向量x处的值为：

$Q(x)=X^{T}AX$

其中矩阵A是一个对称矩阵，矩阵A称为关于二次型的矩阵。

二次型是为研究二次函数或二次多项式而生，这样就能理解《线性代数及其应用》中二次型的定义，以及一些二次型的性质。

二：规范化

二次型或二次齐次方程有着显著的几何意义，一个二元二次函数是二维空间的一个圆，椭圆或双曲线：

$x^{2}+y^{2}=1$ 的一个圆，可以表示为 $\begin{bmatrix} x & y \end{bmatrix}\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}\begin{bmatrix} x\\y \end{bmatrix}=1$ ：

$x^{2}+\frac{1}{4}y^{2}=1$ 的椭圆可以表示为 $\begin{bmatrix} x & y \end{bmatrix}\begin{bmatrix} 1 & 0\\ 0 & \frac{1}{4} \end{bmatrix}\begin{bmatrix} x\\y \end{bmatrix}=1$ ：

一个 $x^{2}-y^{2}=1$ 的双曲线可以表示为 $\begin{bmatrix} x & y \end{bmatrix}\begin{bmatrix} 1 & 0\\ 0 & -1 \end{bmatrix}\begin{bmatrix} x\\y \end{bmatrix}=1$ ：

这样一看，圆，椭圆，双曲线是线性关系，通过矩阵变换可以相互转化，准确说是一种仿射，它们都是圆锥体与平面的交线，所以统称为圆锥曲线。

对于一个倾斜的椭圆 $\frac{5}{8}x^{2}-\frac{3}{4}xy+\frac{5}{8}y^{2}=1$ ，要将其扶正

除了通过坐标变化，解析几何的方法外，可以对其二次型矩阵，进行特征值分解：

a = np.array([[5/8, -3/8], [-3/8, 5/8]])
eval_sigma1,evec_u = np.linalg.eigh(a)

其特征值为： $\begin{bmatrix} 1 & 0\\ 0& \frac{1}{4} \end{bmatrix}$ ，而这个矩阵就是椭圆扶正后的二次型矩阵

三：正定二次型

对于一个二次型 $Q$ ：

a.如果对所有的 $x\neq 0$ ，有 $Q(x)>0$ ，则二次型 $Q$ 称为正定的

b.如果对所有的 $x\neq 0$ ，有 $Q(x)<0$ ，则二次型 $Q$ 称为负定的

c.如果 $Q(x)$ 既有正值又有负值，则二次型 $Q$ 称为不定的

d.如果对所有的 $x$ ， $Q(x)\geqslant 0$ ，则 $Q$ 称为半正定的，如果对所有的 $x$ ， $Q(x)\leqslant 0$ ，则 $Q$ 称为半负定的

二次型与矩阵A的特征值的关系：

a.当且仅当矩阵A的特征值全为正数，则二次型 $Q$ 为正定的

b.当且仅当矩阵A的特征值全为负数，则二次型 $Q$ 为负定的

c.当且仅当矩阵A的特征值既有负数又有正数，则二次型 $Q$ 为不定的

由于任意的二次型可以通过二次型矩阵的特征值分解（二次型的矩阵都是对称矩阵，对称矩阵都可以进行特征值分解），来扶正：

$\begin{bmatrix} x_{1} & x_{2} & ... & x_{n} \end{bmatrix}\begin{bmatrix} \lambda_{1} & 0 & 0 & 0\\ 0& \lambda_{2} & 0 & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \lambda_{n} \end{bmatrix}\begin{bmatrix} x_{1}\\ x_{2}\\ \vdots \\ x_{n} \end{bmatrix}$

所以任意的二次型可以转换为上述特征值的表示形式，以方程形式表示为：

$f(x_{1},x_{2},...,x_{n})=\lambda_{1}x_{1}^{2}+\lambda_{2}x_{2}^{2}+...+\lambda_{n}x_{n}^{2}$

当特征值都为正时， $f(x_{1},x_{2},...,x_{n})=\lambda_{1}x_{1}^{2}+\lambda_{2}x_{2}^{2}+...+\lambda_{n}x_{n}^{2}> 0$ 恒成立

当特征值都为负时， $f(x_{1},x_{2},...,x_{n})=\lambda_{1}x_{1}^{2}+\lambda_{2}x_{2}^{2}+...+\lambda_{n}x_{n}^{2}< 0$ 恒成立

当特征值有正有负时， $f(x_{1},x_{2},...,x_{n})$ 的值，正负都有

这样就证明了二次型的矩阵特征值与其二次型的正定关系。

四：文中图片源码

文中的图片使用Python制作，代码如下：

from matplotlib.patches import Ellipse, Circle
import matplotlib.pyplot as plt
import matplotlib
import math
import numpy as npdef picture1():fig = plt.figure()ellip1 = Ellipse(xy = (0.0, 0.0), width = 2, height = 4, angle = -45, facecolor = 'yellow', alpha = 0.3)ellip2 = Ellipse(xy = (0.0, 0.0), width = 2, height = 4, angle = 0, facecolor = 'blue', alpha = 0.3)ax = fig.add_subplot(111)ax.add_patch(ellip1)ax.add_patch(ellip2)ax.spines['right'].set_color('none')  ax.spines['top'].set_color('none')  ax.spines['bottom'].set_position(('data',0))  ax.spines['left'].set_position(('data',0))  ax.xaxis.set_ticks_position('bottom')ax.yaxis.set_major_locator(matplotlib.ticker.MultipleLocator(1))plt.axis('scaled')plt.show()def Draw_Circle():x = y = np.arange(-2, 2, 0.1)x, y = np.meshgrid(x, y)fig = plt.figure()ax = fig.add_subplot(111)ax.contour(x, y, x**2 + y**2, [1], alpha = 0.3)ax.spines['right'].set_color('none')  ax.spines['top'].set_color('none')  ax.spines['bottom'].set_position(('data',0))  ax.spines['left'].set_position(('data',0))  ax.xaxis.set_ticks_position('bottom')ax.yaxis.set_major_locator(matplotlib.ticker.MultipleLocator(1))ax.xaxis.set_major_locator(matplotlib.ticker.MultipleLocator(1))plt.axis('scaled')plt.show()def Draw_ellipse():a = math.cos(-math.pi/4)b = math.sin(-math.pi/4)x = y = np.arange(-3, 3, 0.1)x, y = np.meshgrid(x, y)fig = plt.figure()ax = fig.add_subplot(111)ax.contour(x*a + y*b, x*b - y*a, x**2 + (1/4)*y**2, [1], alpha = 0.3)ax.contour(x, y, x**2 + (1/4)*y**2, [1], alpha = 0.3)#ax.contour(x, y, x**2 + y**2, [1], alpha = 0.3)#ax.contour(x, y, (5/8)*x**2 - (3/4)*x*y + (5/8)*y**2, [1], alpha = 0.3)ax.spines['right'].set_color('none')  ax.spines['top'].set_color('none')  ax.spines['bottom'].set_position(('data',0))  ax.spines['left'].set_position(('data',0))  ax.xaxis.set_ticks_position('bottom')ax.yaxis.set_major_locator(matplotlib.ticker.MultipleLocator(1))ax.xaxis.set_major_locator(matplotlib.ticker.MultipleLocator(1))plt.axis('scaled')plt.show()def Draw_hyperbola():a = [i / 100 for i in range(100, 300, 1)]b = [math.sqrt(i**2 - 1) for i in a]fig = plt.figure()ax = fig.add_subplot(111)ax.plot(a, b, color = "blue", alpha = 0.3)ax.plot(a, [-i for i in b], color = "blue", alpha = 0.3)ax.plot([-i for i in a], b, color = "blue", alpha = 0.3)ax.plot([-i for i in a], [-j for j in b], color = "blue", alpha = 0.3)ax.spines['right'].set_color('none')  ax.spines['top'].set_color('none')  ax.spines['bottom'].set_position(('data',0))  ax.spines['left'].set_position(('data',0))  ax.xaxis.set_ticks_position('bottom')ax.yaxis.set_major_locator(matplotlib.ticker.MultipleLocator(1))plt.show()if __name__ == "__main__":a = np.array([[5/8, -3/8], [-3/8, 5/8]])eval_sigma1,evec_u = np.linalg.eigh(a)print(eval_sigma1)print(evec_u)Draw_ellipse()