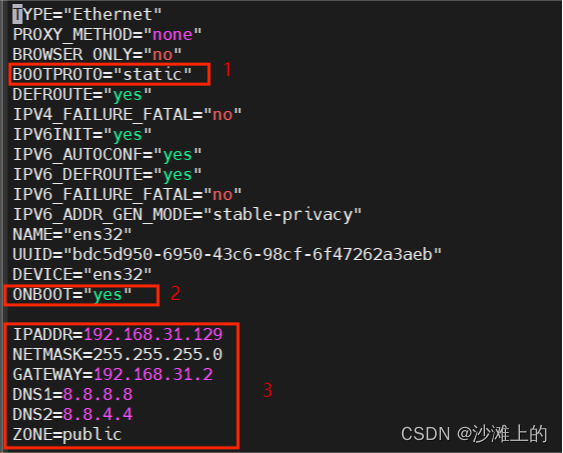
一、网络环境查看命令

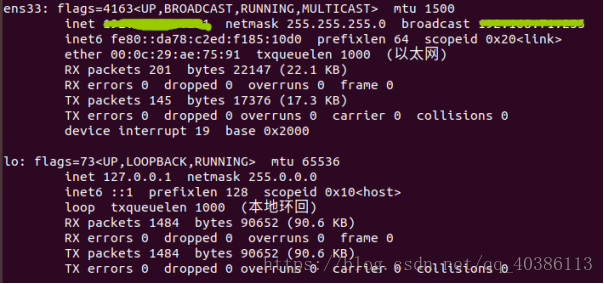
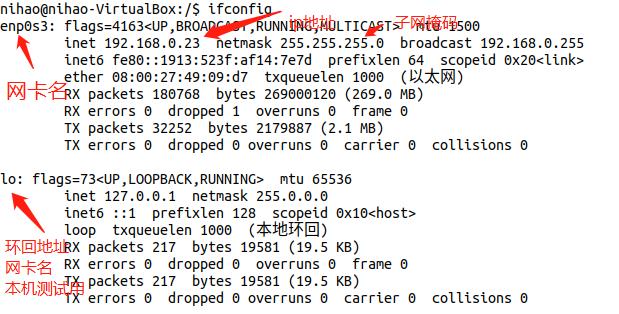
1、ifconfig命令

查看与配置网络状态命令

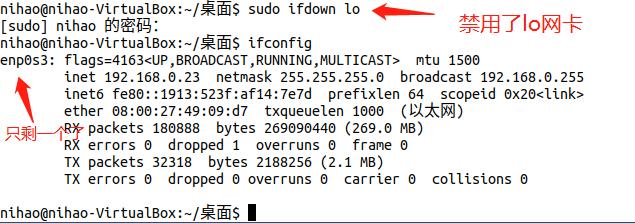
2、ifdown 网卡名

ifdown lo #禁用网卡

3、ifup 网卡名

ifup lo # 启用网卡名是lo网卡

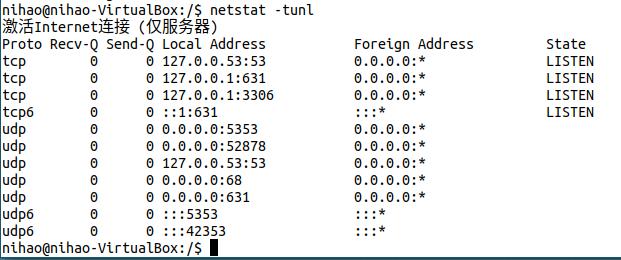
4、netstat

常见的有

netstat -tuln # 后面的选项不分先后

netstat -an # 表示查看所有网络连接

netstat -ant | grep LISTEN # 表示通过管道查找状态是LISTEN的网络

netstat -rn # -r是列出路由列表，可以查看到网关(和route -n命令一样)

5、route -n

查看路由列表(查看到网关)

route add default gw 192.168.1.1 # 设置临时网关

route del default gw 192.168.1.1 # 删除网关

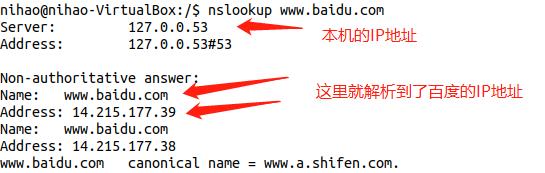
6、nslookup 主机名或IP

进行域名与IP地址解析

例如：nslookup www.baidu.com

二、网络测试命令

1、ping IP或域名

探测指定IP或域名的网络状况

例如：ping www.baidu.com # linux下会一直发数据

加上指令-c就会指定ping包的次数

ping www.baidu.com -c 3

2、telnet [域名或IP] [端口]

远程管理与端口探测命令

例如：telnet 192.168.0.252 80 # 查看该ip地址有没有开放80端口

现在的机器上都默认不开启telnet服务，原因是不安全

3、traceroute [选项] IP或域名

路由跟踪命令

[选项]：-n 使用IP,不使用域名，速度更快

例如：tracetoute www.baidu.com #跟踪传输过程的每个路由

4、wget 下载命令

wget 下载网址

5、tcpdump 网络抓包命令