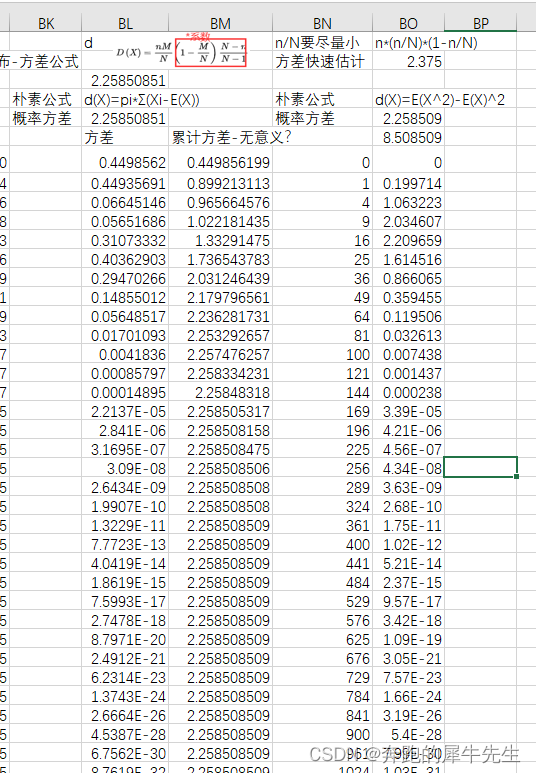
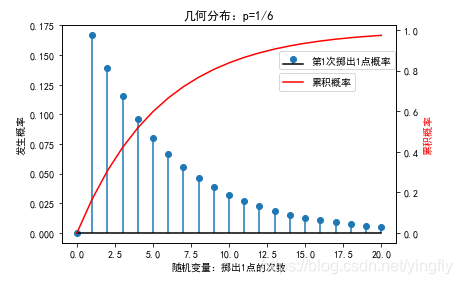
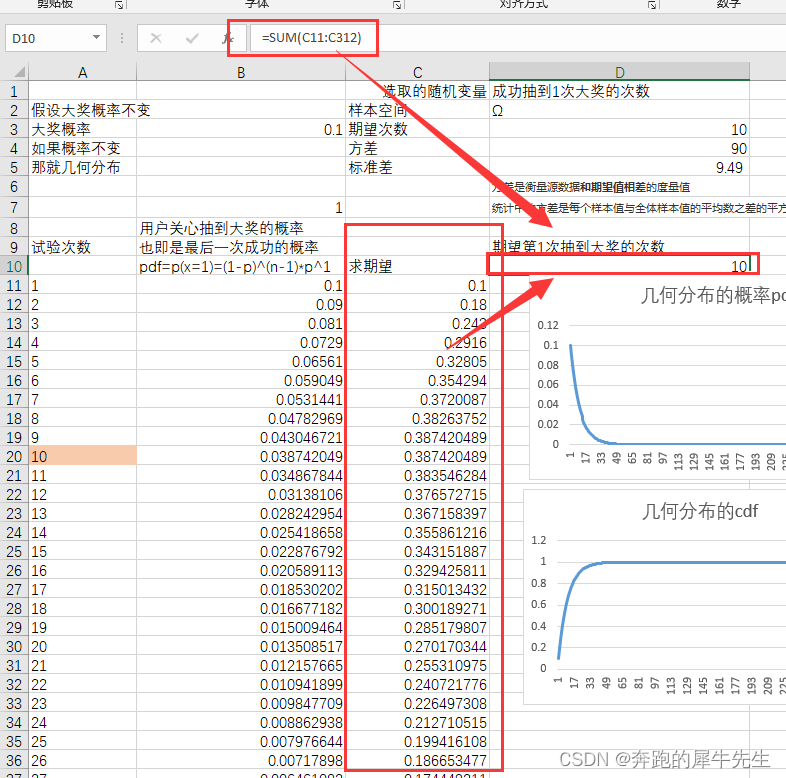
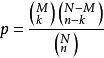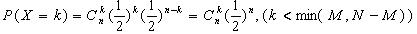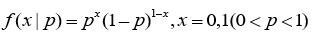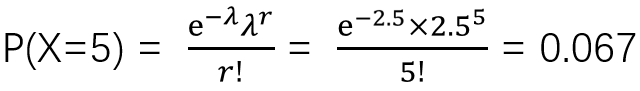css的animation中,有一种描述动画变化速率的东西,例如常见的linear,ease-in,ease-out等,这些都是连续的变化,还有一种叫做steps的,它用来描述一种不连续的动画,也就是逐帧动画。
基本认识
steps的格式为:
- animation-timing-function : steps(number,[end | start])
steps的变化如下图:
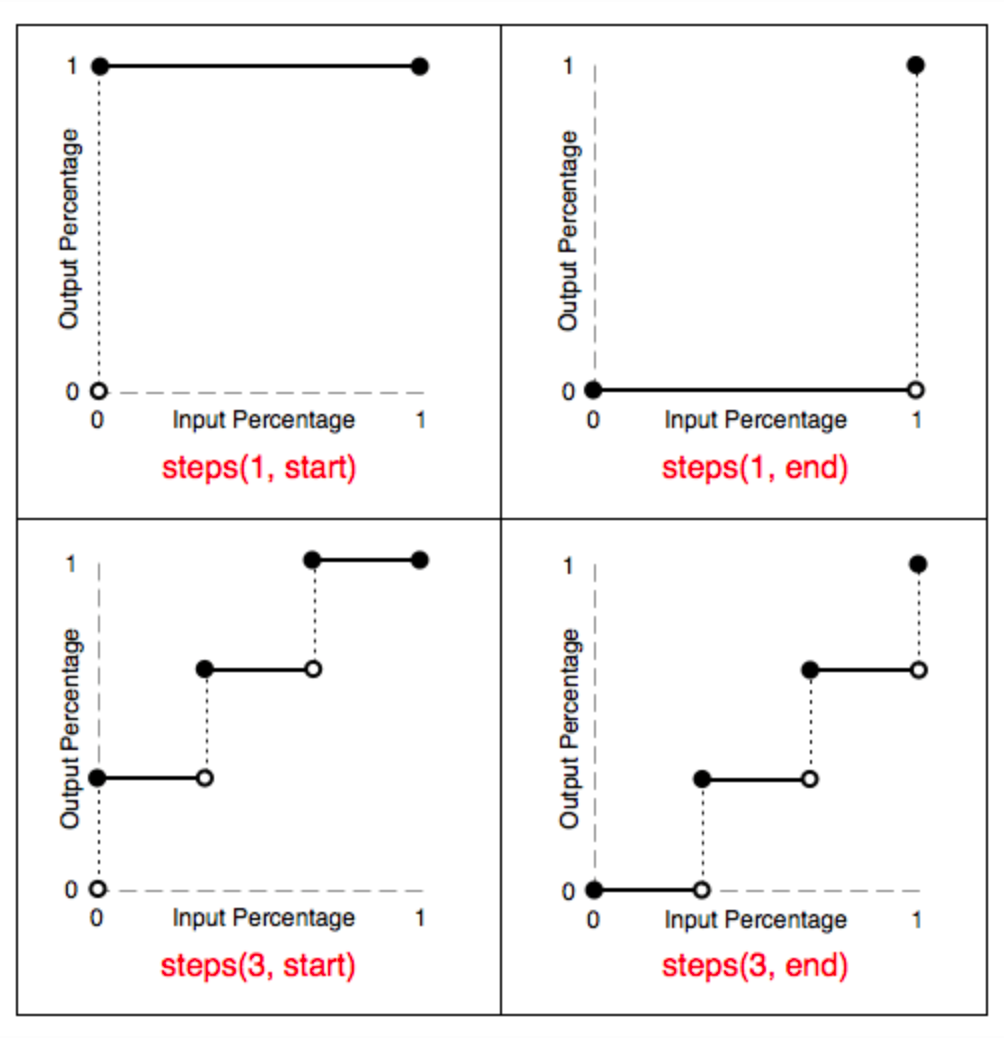
这个图,我相信大家肯定都看过,但是这个图,很容易让人产生误解,steps中的number,指的是走了number步,但是实际上呢,却是将整个动画分成了number+1份。
例如number为3,它其实是将一个连续的动画,分成了4份:
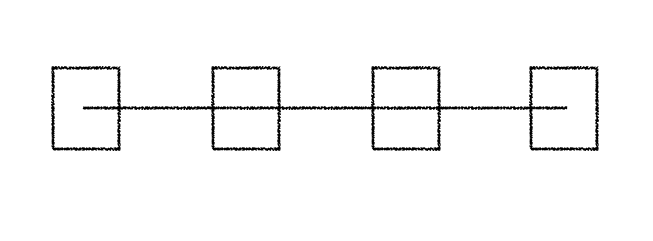
它这种效果,其实有点像快照,在一个连续的动画上,截取均匀的4个位置快照。
它的第二个参数为start或者end,表示舍弃哪个截图:
如果为start,表示舍弃第一个截图:
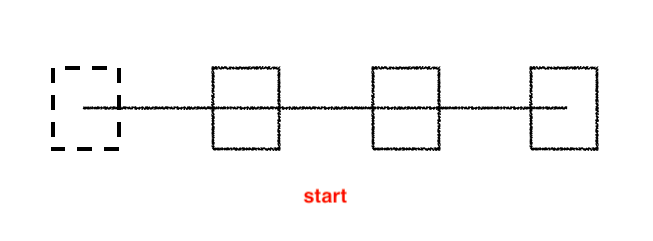
那么只会播放第2,3,4个截图。
如果为end,表示舍弃最后一个截图:
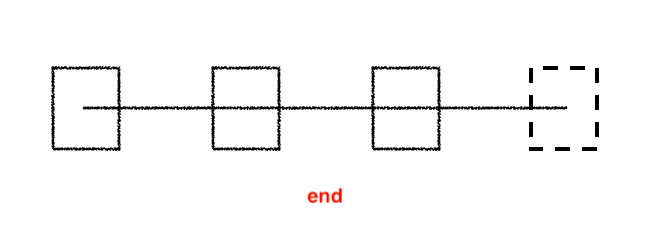
那么只会播放第1,2,3个截图。
也就是说,动画被分成了n+1份,但是实际上,只走了n份,start代表去首,end代表去尾。
需要特别注意的是number为1的情况,它截取的是[0,1]位置的,我开始以为是截取的[0,1/2]位置,测试后发现并不是,切记,截取的是两头的快照:
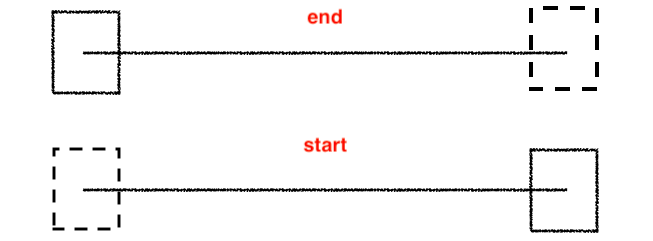
steps-start等价于steps(1,start),只播放最后的快照;steps-end等价于steps(1,end),只播放开头的快照。
实例说明
为了说明这个问题,我做了个demo,让我们一起来仔细讨论下关于steps的问题,我们先看图:

steps动画(二维码)
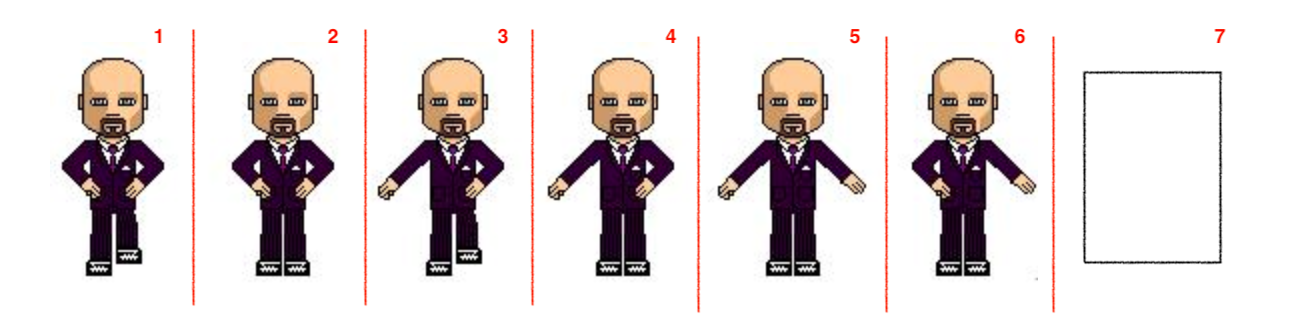
上面是使用steps分布动画制作的效果,它的原图是这样的:

我们看到,图片上有6个小人,分别代表不同的动作,连在一起就是动图效果。
我们看上图,steps的number改设置为多少呢?上面说到,连续的动画实际被分成了number+1分,因此number应该为5,划分成6分:
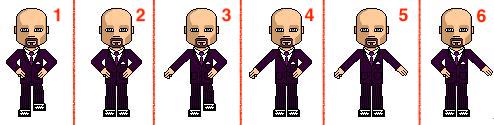
css如下:
#rect{width:76px;height:125px;border:1px solid black;background:url('step.jpg') no-repeat left center;animation:move infinite 2s steps(5,start) ;
}
@keyframes move{0%{background-position:0%;}100%{background-position:100%;}
}一切看起来很正常,很完美,但是这样播放,我们会发现少了一帧,what?
虽然图片分成了6分,但是实际上只走了5步啊!!如果为start,那么走的就是2,3,4,5,6;如果为end,走的就是1,2,3,4,5。因此不管怎么走,其实都会少了一帧。
设置start
正确的做法是,将number设置为6,生成7个快照,如果设置为start,表示丢弃第一个快照:
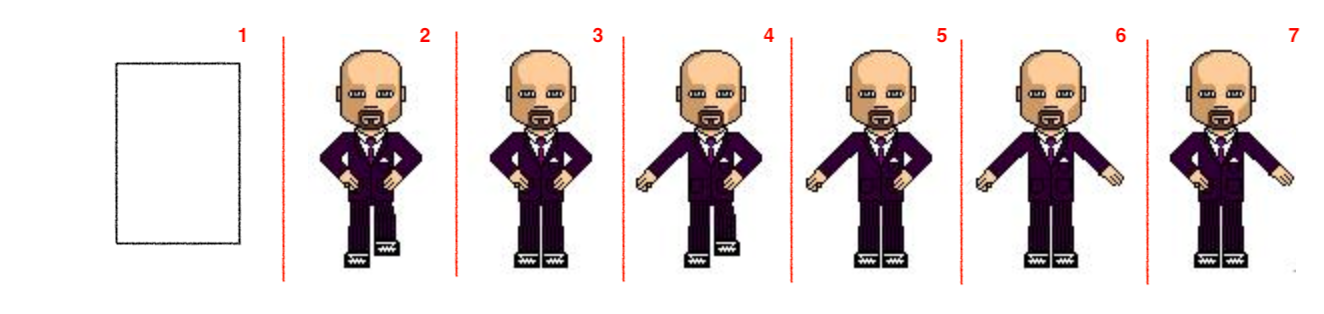
#rect{width:76px;height:125px;border:1px solid black;background:url('step.jpg') no-repeat left center;animation:move infinite 2s steps(6,start) ;
}
@keyframes move{0%{background-position:-22%;/*注意这里*/}100%{background-position:100%;}
}这里需要注意,background-position需要向左移动,移动多少呢?background-position中的百分比为容器和背景图片差*percent,可以参考:css中background-position百分比原理。
这里容器宽高为一个小人,因此容器和背景差为6个小人,因此背景需要向左扩充1/6=16.7%,这里设置-22%,因此背景人物分布不均匀,因此稍微一动了一些。
设置为start,表示丢弃第一个快照,因此只播放2,3,4,5,6,7快照,可以完整播放。
设置end
我们还可以在尾部添加一个空白人物:
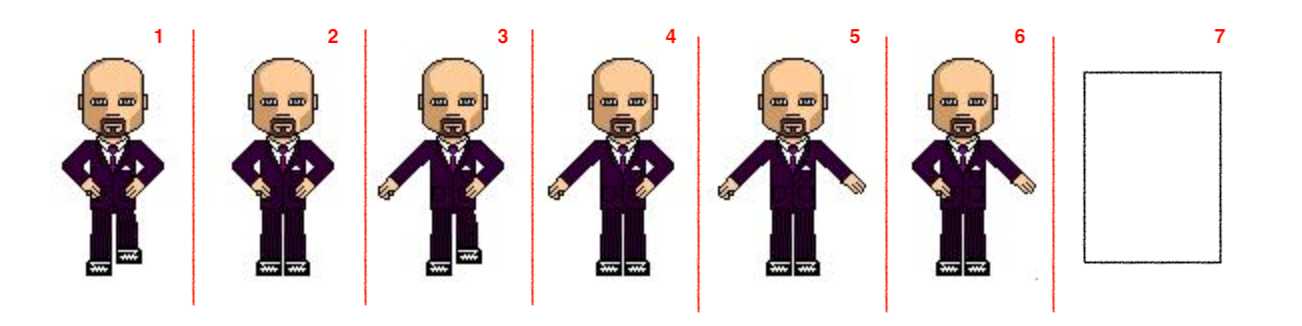
#rect{width:76px;height:125px;border:1px solid black;background:url('step.jpg') no-repeat left center;animation:move infinite 2s steps(6,end) ;
}
@keyframes move{0%{background-position:0%;}100%{background-position:122%;/*注意这里*/}
}注意,这里的background-position需要向右扩充16.7%左右,增加一个空白人物。
设置为end,丢弃最后一个,只播放1,2,3,4,5,6,可以完整播放。
number为其他的情况
steps中number为1,快照截取的是两头的,不是从中间截取的:
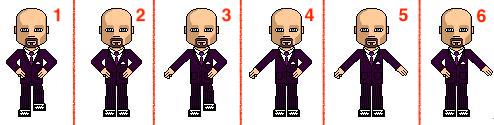
#rect{width:76px;height:125px;border:1px solid black;background:url('step.jpg') no-repeat left center;animation:move 1 2s steps(1,start) ;
}
@keyframes move{0%{background-position:0%;}100%{background-position:100%;}
}例如上面的代码,将会播放的是图6,因为截取的有两个快照,1和6,1被舍弃了,因此只会播放6。
如果设置end,那么只会播放图1。
steps中number为2:
#rect{width:76px;height:125px;border:1px solid black;background:url('step.jpg') no-repeat left center;animation:move 1 2s steps(2,end) ;
}
@keyframes move{0%{background-position:0%;}100%{background-position:122%;}
}有3个快照,分别是1,4,7。
如果设置为end,只会播放1,4;如果设置为start,只会播放4,7。
animation-fill-mode:forwards
这里需要注意一个问题,就是当我们只播放一次,并且设置播放停在最后一帧的时候,如果我们设置steps为end,就会停在丢弃的那一帧上:

例如上图,我们设置css如下:
#rect{width:76px;height:125px;border:1px solid black;background:url('step.jpg') no-repeat left center;animation:move 1 2s steps(5,end) ;
}
@keyframes move{0%{background-position:0%;}100%{background-position:100%;}
}如果正常播放,第6帧会被丢弃掉,播放完,停在第一帧,但是如果你设置了forwrads:
#rect{width:76px;height:125px;border:1px solid black;background:url('step.jpg') no-repeat left center;animation:move 1 2s steps(5,end) forwards;
}
@keyframes move{0%{background-position:0%;}100%{background-position:100%;}
}那么将会停在丢弃的第6帧上,这个需要特别注意。
转载于:http://www.qiutianaimeili.com/html/page/2021/06/2028tl9nhl7wfij.html