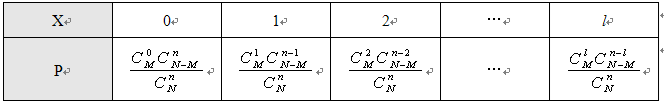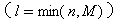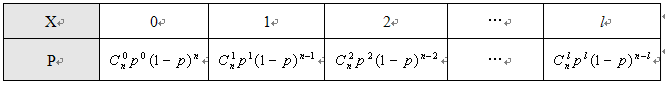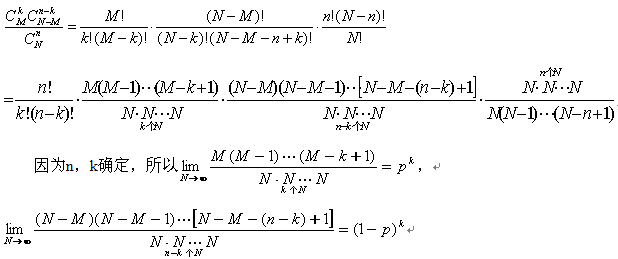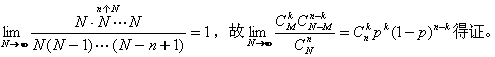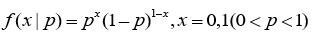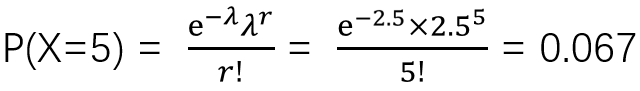超几何分布与二项分布的联系与区别

事实上,超几何分布和二项分布确实有着密切的联系，但也有明显的区别。
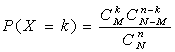
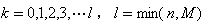
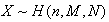
　　课本对于超几何分布的定义是这样的：一般的，若一个随机变量X的分布列为，其中，则称X服从超几何分布，记为。其概率分布表为：
　    
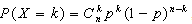
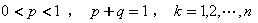
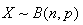
　　对于二项分布的定义是这样的：若随机变量X的分布列为,其中则称X服从参数为n,p的二项分布，记为。其概率分布表为：
　   
　　超几何分布与二项分布都是取非负整数值的离散分布，表面上看，两种分布的概率求取有截然不同的表达式，但看它们的概率分布表，会发现构造上的相似点，如：随机变量X的取值都从0连续变化到l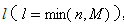，对应概率和N,n,l三个值密切相关……可见两种分布之间有着密切的联系。对超几何分布的模型建立是这样的：若有N件产品，其中M件是废品，无返回地任意抽取n件，则其中恰有的废品件数X是服从超几何分布的。而对二项分布则使用比较容易理解的射击问题来建立模型。若将但超几何分布的概率模型改成：若有N件产品，其中M件是废品，有返回的任意抽取n件，则其中恰有的废品件数X是服从二项分布的。在这里，两种分布的差别就在于"有"与"无"的差别，只要将概率模型中的"无"改为"有"，或将"有"改为"无"，就可以实现两种分布之间的转化。"返回"和"不返回"就是两种分布转换的关键。
　　看例题：高三（1）班的联欢会上设计了一项游戏：在一个口袋中装有10个红球、20个白球，这些球除颜色外完全相同，一次从中摸出5个球，摸到4个红球1个白球就是一等奖，求获一等奖的概率。本题采用的解法是摸出球中的红球个数X服从超几何分布，但是如果将"一次从中摸出5个球"改为"摸出一球记下颜色，放回后再摸一球，反复5次"，则摸出球中的红球个数X将不再服从超几何分布，而是服从二项分布。
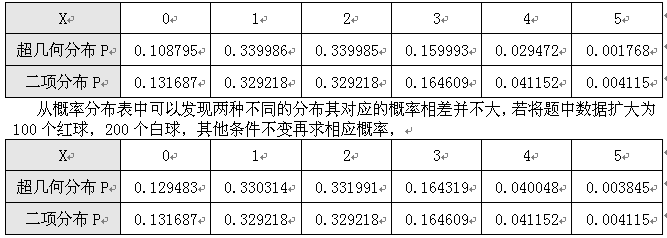
　　我们分别来计算两种分布所对应的概率：

       
　　这时发现发现两种不同的分布其对应的概率之间的差距进一步缩小了，我们做出这样的猜想：样本个数越大超几何分布和二项分布的对应概率相差就越小，当样本个数为无穷大时，超几何分布和二项分布的对应概率就相等，换而言之超几何分布的极限就是二项分布！也就是说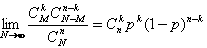。下面我们对以上猜想作出证明：
　　产品个数N无限大，设废品率为p，则，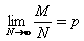

       
　　
　　以上的证明与我们的直观思想相吻合：在废品为确定数M的足够多的产品中，任意抽取n个（由于产品个数N无限多，无返回与有返回无区别，故可看作n次独立试验）中含有k个废品的概率当然服从二项分布。在这里，超几何分布转化为二项分布的条件是（1）产品个数应无限多，否则无返回地抽取n件产品是不能看作n次独立试验的.(2）在产品个数N无限增加的过程中，废品数应按相应的"比例"增大，否则上述事实也是不成立的。
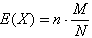
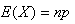
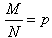
　　对于超几何分布的数学期望，二项分布的数学期望，当我们将"不返回"改为"返回"时，，两种分布的数学期望相等，方差之间没有相等关系。超几何分布和二项分布的数学期望和方差是否也具有我们以上猜想并证明的极限关系呢？
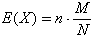
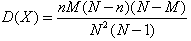
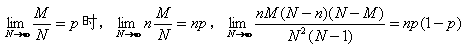
　　事实上超几何分布的数学期望，方差当这两个极限值分别是二项分布的数学期望与方差。需要指明的是这一性质并非只为超几何分布与二项分布之间所具有，一般地，如果随机变量依分布收敛于随机变量，则随机变量的数学期望和方差分别是随机变量的数学期望和方差的极限。这样超几何分布与二项分布达到了统一。
　　一般说来，有返回抽样与无返回抽样计算的概率是不同的，特别在抽取对象数目不大时更是如此。但当被抽取的对象数目较大时，有返回抽样与无返回抽样所计算的概率相差不大，人们在实际工作中常利用这一点，把抽取对象数量较大时的无返回抽样（例如破坏性试验发射炮弹；产品的寿命试验等），当作有返回来处理。
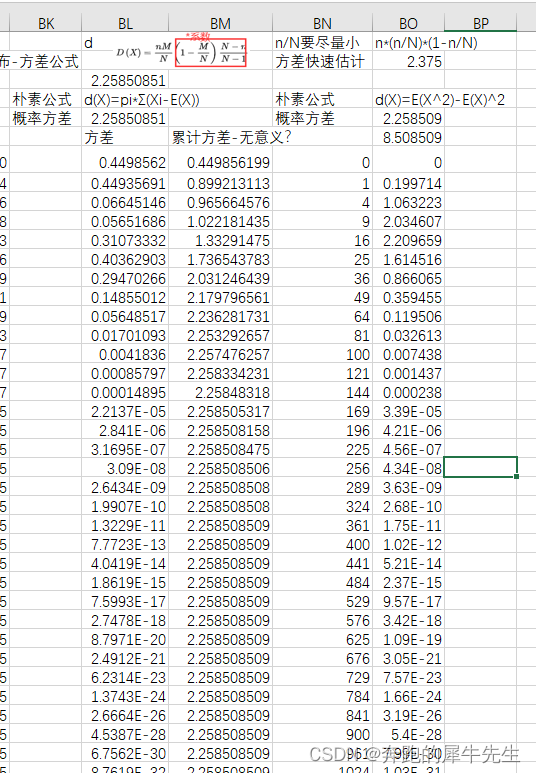
　　那么，除了在有无"返回"上做文章，有没有什么办法快速实现超几何分布向二项分布的转化呢？
　　设想N件产品装在一个大袋中，其中M件为废品，无返回地从中抽取n件，那么其中废品件数 X服从超几何分布。现若在大袋中再放进两个小袋，一袋装正品，一袋装废品，然后从大袋中任摸一个小袋，无返回地从中任取一件产品，则这样任取n件，其中废品件数X就不再服从超几何分布，而应服从的二项分布了。事实上，我们把摸到正品袋中的产品看作"成功"，摸到废品袋中的产品看作"失败"，则"成功"与"失败"的概率相等，皆为且每次试验是相互独立的，正是典型的伯努力试验概型，因此可用二项分布去刻划其概率分布列。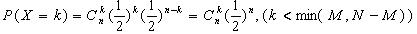,从这一点上讲，两种分布仅"一袋之隔"。将正品和废品隔离，则超几何分布将成为二项分布。
　　超几何分布和二项分布这两种离散型随机变量的概率分布表面上看来风马牛不相及，但通过以上的论证，我们发现这两种分布可以通过有无"返回"，隔离正品和次品等方法来互相转换，抛开转换问题，也可把二项分布看作超几何分布的极限，它们的期望和方差之间也存在这种极限关系。