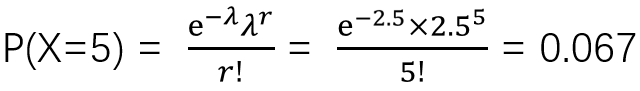概率论与数理统计基础（二）:常用离散分布二项、泊松、超几何分、几何、负二项分布

article/2025/9/18 0:09:54

本文列举了常见的离散分布，关于它们的背景、概率分布列、数学期望与方差，以及与之相关的一些重要性质；比如几何分布的无记忆性、二项分布的泊松近似、超几何分布的二项近似。。。。可作为离散分布的知识速查表。

1. 二项分布b(n,p)

2. 泊松分布 $P\left ( \lambda \right )$

3 超几何分布 $h\left ( n,N,M \right )$

4 几何分布 $Ge\left ( p \right )$

5 负二项分布 / 巴斯卡分布 $Nb\left ( r,p \right )$

6 常用离散分布表

1. 二项分布b(n,p)

背景：在n重伯努利实验中成功的次数服从二项分布b(n,p),其中p为一次伯努利实验中成功发生的概率， $0< p< 1$ .
概率分布列： $P\left ( X=k \right )=\binom{n}{k}p^{k}\left ( 1-p \right )^{n-k}$
n=1 时，二项分布退化为二点分布【0-1分布】
二项分布b(n,p) 的数学期望为 $E\left ( X \right )=np$ , 方差为 $Var\left ( X \right )=np\left ( 1-p \right )$
若 $X\sim b\left ( n,p \right )$ ,则 $Y=n-X\sim b\left ( n,1-p \right )$ , 其中 $Y=n-X$ 是在n重伯努利实验中失败的次数

2. 泊松分布 $P\left ( \lambda \right )$

背景：单位时间【或单位面积、单位产品等】上稀有事件【不经常发生的事件】发生的次数
概率分布列： $P\left ( X=k \right ) =\frac{\lambda ^{k}}{k!}e^{-\lambda } ;\: k=0,1,2,...$
$E\left ( X \right )=\lambda ;\: \: Var\left ( X \right ) =\lambda$
二项分布的泊松近似（泊松定理）

在n重伯努利实验中，记事件A在一次伯努利实验中发生的概率为 $p_{n}$ （与试验次数n有关）,如果当 $n\rightarrow +\infty$ 时，有 $np_{n}\rightarrow \lambda$ , 则 $\lim_{n\rightarrow +\infty}\binom{n}{k}p_{n}^{k}\left ( 1-p_{n} \right )^{n-k}=\frac{\lambda ^{k}}{k!} e^{-\lambda }$

3 超几何分布 $h\left ( n,N,M \right )$

背景：从含有M个不合格产品的N个产品中，不放回地随机抽取n个，则其中含有的不合格品的个数服从超几何分布。
概率分布列: $P\left ( X=k \right ) =\frac{ \binom{M}{k}\binom{N-M}{n-k} }{\binom{N}{n}}, k=0,1,...,r$ ,其中 $r=min\left \{ M,n \right \};\: \: M\leqslant N;\, n\leqslant N$ 且 $n,M,N$ 均为正整数
期望与方差： $E\left ( X \right )=n\frac{M}{N} ;Var\left ( X \right )=\frac{nM\left ( N-M\right )\left ( N-n \right ) }{N^{2}\left ( N-1 \right )}$
超几何分布的二项近似：当 $n< < N$ , 超几何分布 $h\left ( n,N,M \right )$ 可用二项分布 $b\left ( n, \frac{M}{N} \right )$ 近似，即

$\frac{ \binom{M}{k}\binom{N-M}{n-k} }{\binom{N}{n}} = \binom{n}{k}p^{k}\left ( 1-p \right )^{n-k}$ , 其中 $p=\frac{M}{N}$ .

实际应用：当批量N较大、而抽出样品数n较小时，不返回抽样可看作返回抽样的近似。

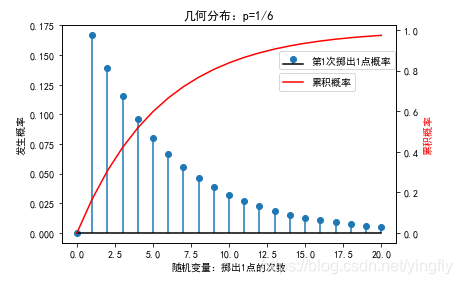
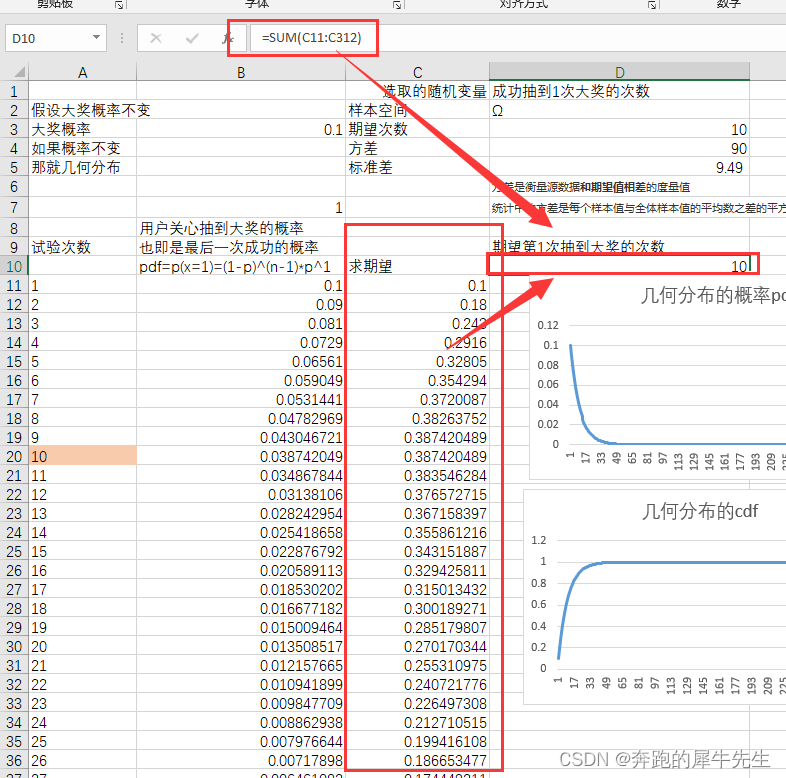
4 几何分布 $Ge\left ( p \right )$

背景：在伯努利试验序列中，成功事件A首次出现时的试验次数, p为每次试验中事件A发生的概率
概率分布列： $P\left ( X=k \right ) =\left ( 1-p \right )^{k-1}p\: \: ;\: k=1,2,..$
期望与方差: $E\left ( X \right )=\frac{1}{p}\: ;\: Var\left ( X \right )=\frac{1-p}{p^{2}}$
几何分布的无记忆性

若 $X\sim Ge\left ( p \right )$ ,则对任意正整数m与n有: $P\left ( X> m+n\: |\: X> m \right )=P\left ( X> n \right )$

5 负二项分布 / 巴斯卡分布 $Nb\left ( r,p \right )$

背景：在伯努利试验序列中,成功事件A第r次出现时的试验次数,
概率分布列： $P\left ( X=k \right )=\binom{k-1}{r-1}p^{r}\left ( 1-p \right )^{k-r} \: ;\: k=r,r+1,..$
期望与方差: $E\left ( X \right )=\frac{r}{p}\: ;\: Var\left ( X \right )=\frac{r\left ( 1-p\right )}{p^{2}}$
几何分布与负二项分布的关系: r=1时的负二项分布为几何分布，即 $Nb\left ( 1,p \right ) =Ge\left ( p \right )$