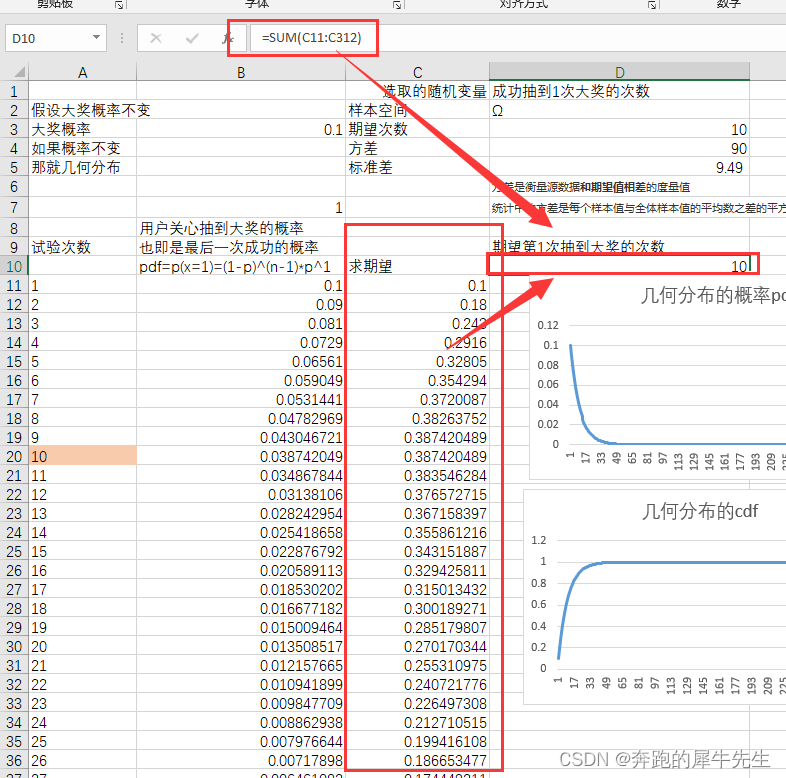
几何分布
几何分布用于描述这种分布:独立事件的结果只有2个:”1和0“ 或”成功和失败“等,成功的概率为 p p p, 失败的概率为 q = 1 − p q=1-p q=1−p; 第r次成功的概率为
P ( X = r ) = p ⋅ q r − 1 P(X=r)=p\cdot q^{r-1} P(X=r)=p⋅qr−1
即用来描述进行多次伯努利事件,第1次成功次数的概率;换句话说每一次事件都有成功和失败的可能,所关心的是第一次成功的概率或取得第一次成功需要试验的次数。
期望 : E ( X ) = 1 p \displaystyle E(X)=\frac {1}{p} E(X)=p1
方差: D ( X ) = E ( X − E ( X ) ) = p q 2 \displaystyle D(X)=E(X-E(X)) = \frac {p}{q^2} D(X)=E(X−E(X))=q2p
由几何分布密度函数可以得出第1, 2, 3, … , k,k+1, …发生的概率为比例系数为q的等比数列,即:
p , p q , p q 2 , . . . , p q k − 1 , p q k , . . . p,\ pq, \ pq^2,\ ..., pq^{k-1}, \ pq^k, \ ... p, pq, pq2, ...,pqk−1, pqk, ...
P ( X = k + 1 ) P ( X = k ) = q \displaystyle \frac {P(X=k+1)}{P(X=k)}=q P(X=k)P(X=k+1)=q
一种说法是等比数列又被称为几何数列,故该分布称为几何分布。
性质
-
任何几何分布的众数为1, 看似违反直觉,但第1次成功的概率最大;
-
大于r次成功的概率,即前r次均失败,为 P ( X > r ) = q r \large P(X>r)=q^r P(X>r)=qr
-
小于等于r次成功的概率,即 P ( X ) ≤ 1 − q r \large P(X)\le 1-q^r P(X)≤1−qr, 其实就是等比数列求和:
P ( X ≤ r ) = ∑ n = 0 r p ⋅ q n − 1 = p ( 1 − q r ) 1 − q = 1 − q r \large P(X\le r) = \sum_{n=0}^r{p\cdot q^{n-1}=\frac{p(1-q^r)}{1-q}} = 1-q^r P(X≤r)=n=0∑rp⋅qn−1=1−qp(1−qr)=1−qr
举例
掷色子,1-6点的概率均为1/6,掷出1点算赢,其它点算输,记 X为第一次掷出赢的次数,则:
P ( X = r ) = p q r − 1 \Large P(X=r)=pq^{r-1} P(X=r)=pqr−1
其中p为1/6, q为5/6。
scipy.stats 中有geom模块,可以方便的计算各种参数:
"""po = stats.poisson(mu) #用于构造均值与μ的泊松分布;
po.pmf(k, mu, loc=0) # Probability mass function. 概率质量函数;
po.cdf(k, mu, loc=0) #Cumulative distribution function.累积分布函数;
po.ppf(q, mu, loc=0) # Percent point function 百分点函数(cdf的倒数-百分位数)。
"""
p=1./6
N=20
x=np.arange(N+1)
po = stats.geom(p) #构造发生概率为p的几何分布
pm = po.pmf(x) #计算第1次发生次数的概率
# 图形
fig = plt.figure()
ax = plt.gca()
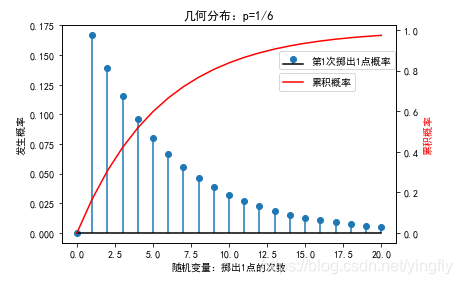
line1 = ax.stem(x,pm,basefmt='k',label='第1次掷出1点概率');
ax.set_xlabel('随机变量:掷出1点的次数');
ax.set_ylabel('发生概率');
ax.set_title('几何分布:p=1/6');ax2=plt.twinx()
y=po.cdf(x) #计算第1次时间发生的累积分布概率
line2 = ax2.plot(x,y,'r',label='累积概率')
ax2.set_ylabel('累积概率',color='r')
ax.legend(loc=(0.65,0.8));
ax2.legend(loc=(0.65,0.7))
# 打印累积发生概率大于等于50%的次数
po.ppf(0.5)
输出为:4.0 。