目录

1超几何分布 Hypergeometric distribution         

1.1 超几何分布的定义

1.2 为什么叫超几何分布 

1.3 超几何分布的公式  （2种公式）

1.3.1 超几何分布的公式1 （总体型公式）

1.3.2 超几何分布的公式2 （拆分型公式）

1.4 超几何分布的分布图

2 超几何分布的期望和方差

3 超几何分布的两端

4 超几何分布和二项分布的距离有多远？

4.1 两者差别

4.2 两者接近的可能

超几何分布的概率，期望，方差等

概率变化时对比图形

概率相关

期望相关

方差相关

---

1超几何分布 Hypergeometric distribution         

1.1 超几何分布的定义

• 超几何分布和几何分布可以说没有关系，只是名称有点像
• 超几何分布的基本特点

1. 超几何分布，是针对，不放回抽样的
2. 超几何分布，也是离散分布
3. 超几何分布的公式： f(k,n,K,N)   =  C(k,K) * C(n-k,N-K) / C(n,N)     

1.2 为什么叫超几何分布 

• 称为超几何分布，是因为其形式与“超几何函数”的级数展式的系数有关。
• 其实就是展开形式，不是等比，而是一个关于x的函数      
• f(k,n,K,N)   =  C(k,K) * C(n-k,N-K) / C(n,N)       
• f(x=k)    =    C(a,K) * C(b,N-K) / C(a+b,N)        
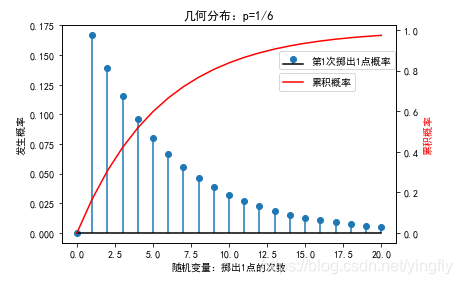
• 几何分布得两项之间，呈现1个等比关系（也就是几何（平均数）关系）
• 超几何数列即每项与前一项之比为项数n的简单函数（简单函数就是指组合数了）的数列。超几何数列是几何数列的扩展，所以叫“超几何”。 

1.3 超几何分布的公式  （2种公式）

1.3.1 超几何分布的公式1 （总体型公式）

• 超几何分布记作X~H(n,N,k,K) 。                                                 
• f(k,n,K,N)    =    C(k,K) * C(n-k,N-K) / C(n,N)         
• 超几何分布中的参数是k,n,K,N, 这些参数分别是 

1. n 总样本数量
2. N 抽样的样本数量
3. k 样本里特殊类别的总数 （比如次品数，比如黑球里的白球数）
4. K 抽样调查里，预期抽到的特殊类别的数量

• f(k,n,K,N)    =    C(k,K) * C(n-k,N-K) / C(n,N)     
• 公式理解说明
• C(n,N)           在全体n中抽取N个样本的方法数量          
• C(k,K)            在全体的K个指定特殊单位中抽取K个特殊的方法数，即组合数，二项式系数
• C(n-k,N-K)     在n中剩下非特殊的n-k，抽取N-k个的方法数量  
• 其中分母得2个构成：  k  +    n-k  = n      ，都是总体样本的相关概念
• 其中分子得2个构成：  K  +   N-K = N      ，都是抽样样本的相关概念
                              
      

1.3.2 超几何分布的公式2 （拆分型公式）

• 如果直接把 样本总体，分成2种，比如 a个白 ，b个黑    
• 现在要做试验，求取得k个白球的期望         

1. 样本总数= a+b
2. 抽样样本数 N
3. 白球数a ，假设取得K个                             

• f(x=k)    =    C(a,K) * C(a+b-a,N-K) / C(a+b,N)     
• f(x=k)    =    C(a,K) * C(b,N-K) / C(a+b,N)         

1.4 超几何分布的分布图

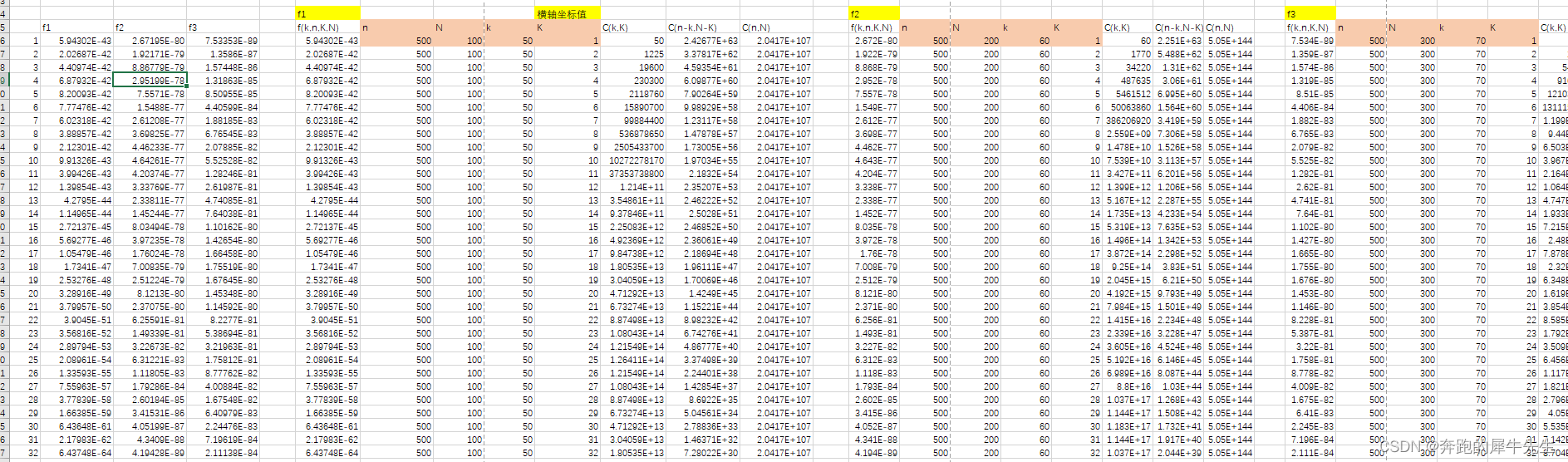
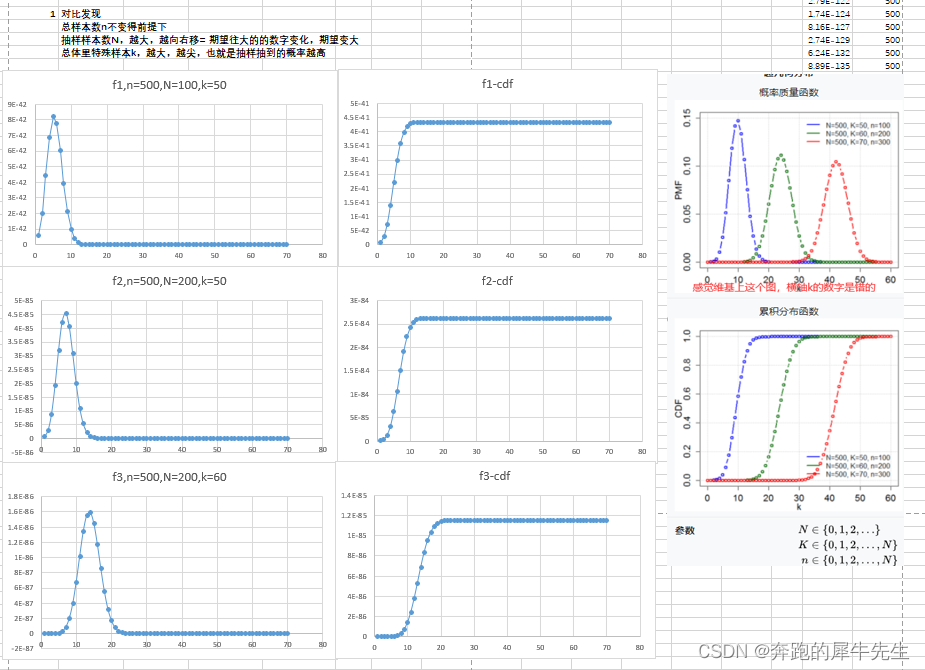
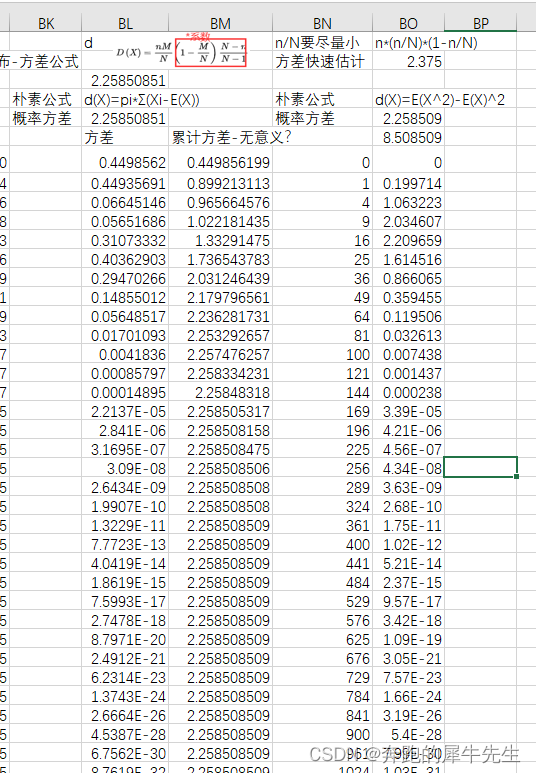
2 超几何分布的期望和方差

超几何分布的期望值计算公式为Ex=nM/N，其中x是样本数，n为样本容量，M为样本总数，N为总体中的个体总数，超几何分布的方差计算公式为Vx=Xn²Pn-a²，其中a为期望值。

超几何分布的期望和方差.pdf-原创力文档

超几何分布的数学期望与方差推导 - 知乎

 甘志国——超几何分布的分布列、期望与方差（解题研究）_腾讯新闻

E(x)=n*M/N

其中N 是总样本数量

n是抽样样本数量

M是要找的次品的总体内个数

x=k是我们要求的随机变量

3 超几何分布的两端

• 超几何分布的各种极限值（或者说退化）
• 如果N=1,退化为伯努利分布，表示只抽1次，无所谓放回不放回了                                 
• 如果样本容量n=1，即从有限总体中只抽取一个个案，且恰好抽到符合要求个案的概率，那么超几何分布可以还原成二项分布。
• 如果每次只抽1个，不放回抽样 = 放回抽样了，二项分布，类正态分布？
• 如果数据总体的容量N无穷大，也就是将有限总体换成无限总体，此时抽中的个案放回与不放回对于总体中符合要求的个案比例都没有影响，超几何分布也可视为二项分布。
• N无穷大，也是不放回抽样 = 放回抽样了，二项分布，类正态分布？
• 在实际应用时，只要数据总体的个案数目是样本容量的10倍以上，即N>10n，就可用二项分布近似描述超几何分布，通过两种概率质量函数计算得到的概率几乎相同
   

4 超几何分布和二项分布的距离有多远？

4.1 两者差别

• 超几何分布，是属于古典概型的
• 二项分布，是属于伯努利试验的，
• 这两者看起来差别很远

4.2 两者接近的可能

• 第1：如果样本数量n 尽量大，趋近无限，那么放回== 不放回，两者就接近了
• 第2：在较小样本量下，两者区别是： 有放回   VS  不放回
• 但是构造一种特殊的题目，可以让两者转化

上面这个改题目来着这里，这个文章写的很好，总结了超几何分布居然可以通过分袋子变成二项分布的题目。。。

https://blog.csdn.net/Eric2016_Lv/article/details/53133244

机器学习小组知识点12：超几何分布（Hyper-Geometric Distribution）_Eric2016_Lv的博客-CSDN博客_超几何分布

超几何分布的概率，期望，方差等

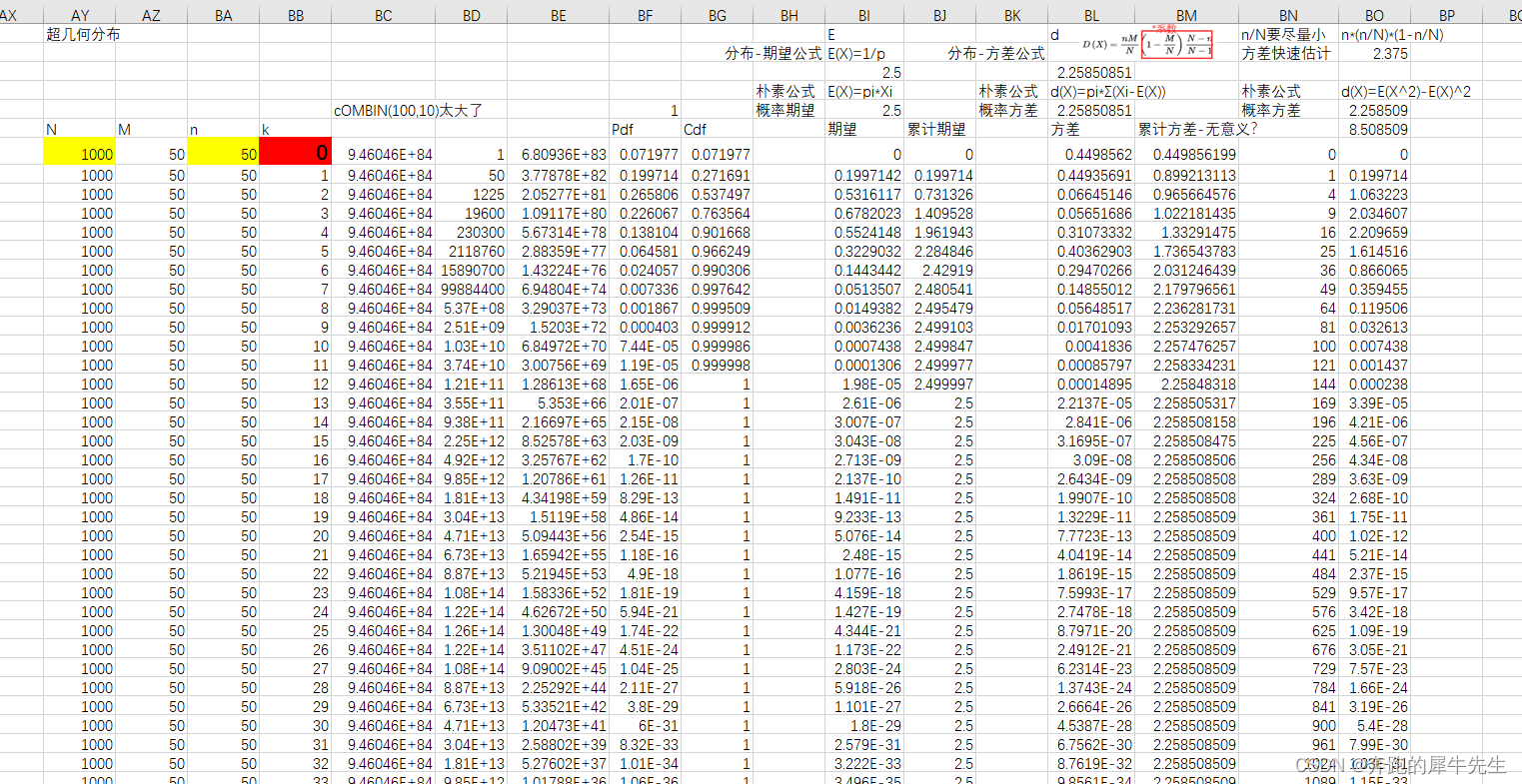
概率变化时对比图形

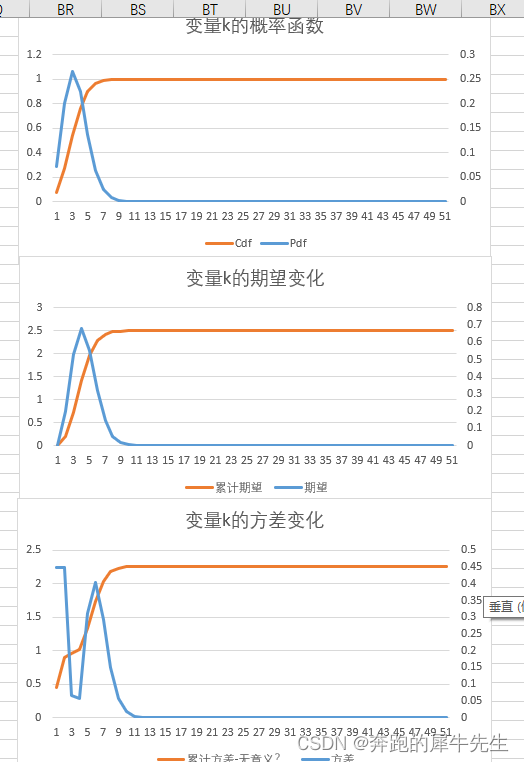
概率相关

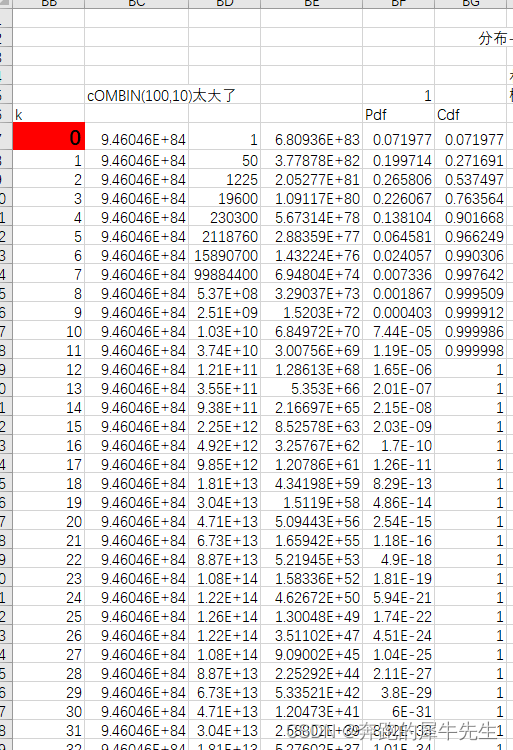
期望相关

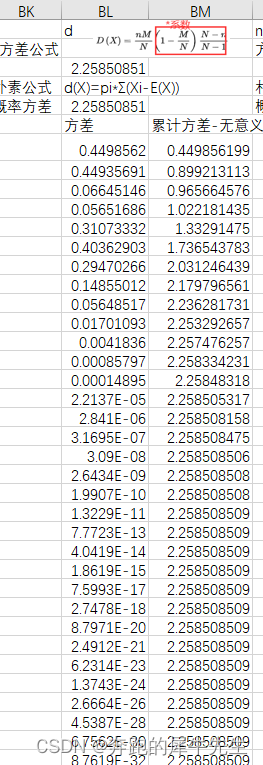
方差相关