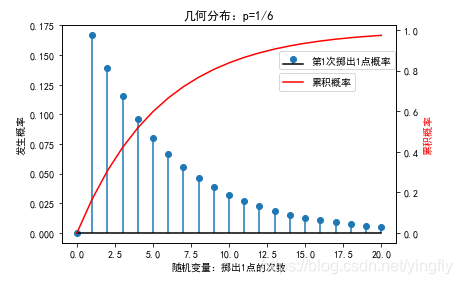
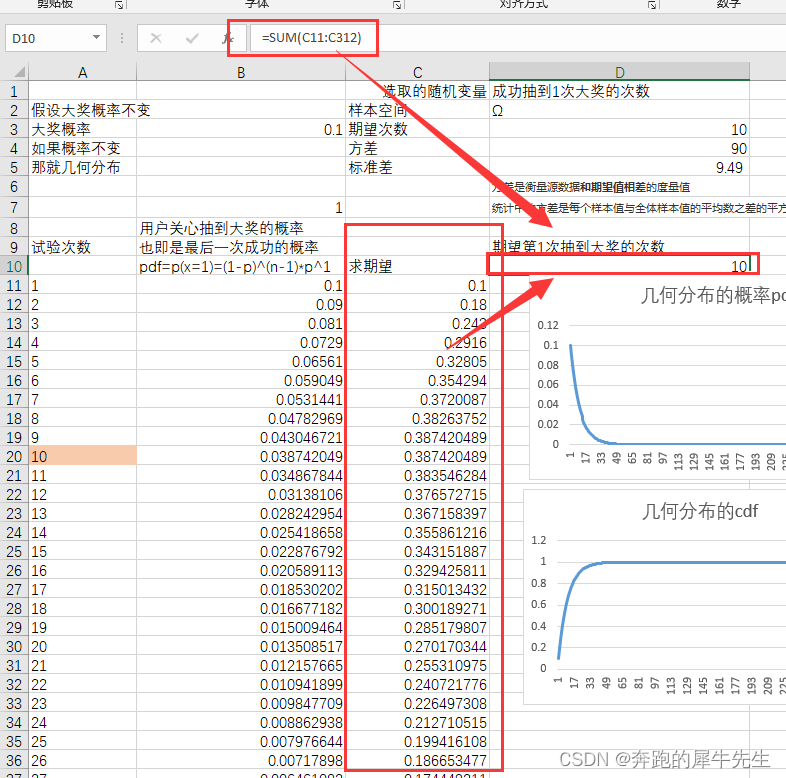
一、几何分布

假设某种赌博游戏的胜率为0.2，那么意味着你玩第一次就胜出的概率为0.2。

那玩第二次才胜出呢？“玩第二次才胜出”就意味着玩第一次是失败的，而直到第二次才胜出，那么这件事发生的概率就是0.8×0.2=0.16。

那么第三次、第四次呢？

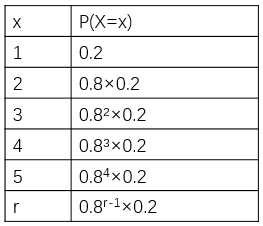
如果用p代表某件事发生的概率，则它不发生的概率为1-p，我们将此概率称为q，于是可以用下式计算任何具有这一性质的概率：

这个公式叫做概率的几何分布。变量X表示为了取得第一次成功所需进行的试验次数，为了在第r次试验时取得成功，首先要先失败r-1次。

几何分布同样适用于不等式。

P(X＞r)指的是为了取得第一次成功需要试验r次以上的概率。为了让需要进行的试验次数大于r，意味着前r次试验必须以失败告终。也就是说，将失败概率乘上r次就是所求的概率：

利用这个，可以求出P(X≤r)，即为了取得一次成功而需要尝试r次或r次以下的概率：

如果一个变量X的概率符合几何分布，且单次试验的成功概率为p，则可以写作：

几何分布的期望模式

在数学期望已知的情况下，就可以得出试验在成功之前需要试验的次数的期望值。

假设X~Geo(0.2)，那么：

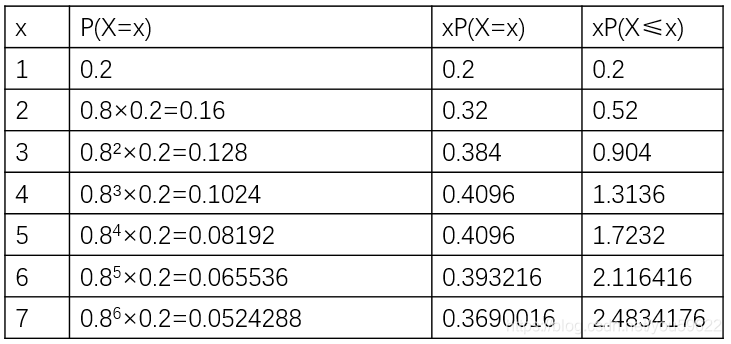
如果将xP(X=x）的累计总和画成图形：

将xP(X=x)的累计总和画成图形后，可以看出，随着x的变大，累计总和越来越接近一个特定数值：5。即：E(X)=5。

上式的意义很直观：单次试验的成功概率为0.2，则可以理解为试验5次中就有一次可能成功。

以上情况可以推而广之任意数值p。如果X~Geo(p)，则：

二、二项分布

假设进行一项试验的成功的概率为0.25，那么连续进行三次试验，用X代表成功的次数，则P(X=0)、 P(X=1)、 P(X=2)、 P(X=3)分别为多少？

很明显能看出规律：x的值与0.25和0.75的幂次存在某种关系。

表中的结果可以用下式来归纳：

进而将此式推广到一般情况：

这类问题被称为二项分布，写作：

并且，只要X~B(n,p)，则：

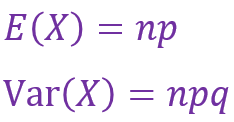
三、泊松分布

假如某台机器一周内发生故障的平均次数为3.4，那么下周这台机器不发生故障的概率有多大？

这一类问题的难点在于，尽管我们知道机器的每周平均故障次数，但实际的故障发生次数却是不固定的，如果倒霉的话，发生故障的次数就会多，如果幸运的话，一次故障都不会发生。这时就需要借助泊松分布来解决这一类问题。

泊松分布包含以下条件：

①单独事件在给定区间内随机、独立地发生；

②已知该区间内的事件平均发生次数（或发生率），且为有限数值。

如果X符合泊松分布，且发生率为λ，则写作：

且：

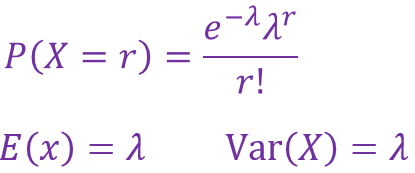
回到刚才的问题，机器在下周不发生故障的概率为多少？

那么下周机器发生三次故障的概率：

如果X~Po (λx)且Y~Po (λy)，则：

再来看下面这道问题：一个学生要参加一场考试，但他没有做任何复习。他需要猜测每一道题的答案，每一题答对的几率为0.05，考卷上共有50个问题，他答对5道题的概率是多少？

这是一道二项分布问题，但如果用二项分布求解，那么幂次会非常之大，计算起来很困难。

而当n很大且p很小时，可以用X~Po(np)近似代替X~B(n,p)。于是：

#转自知乎：

Q：泊松分布的现实意义是什么，为什么现实生活多数服从于泊松分布？
A：先说结论：泊松分布是二项分布n很大而p很小时的一种极限形式
二项分布是说，已知某件事情发生的概率是p，那么做n次试验，事情发生的次数就服从于二项分布。
泊松分布是指某段连续的时间内某件事情发生的次数，而且“某件事情”发生所用的时间是可以忽略的。例如，在五分钟内，电子元件遭受脉冲的次数，就服从于泊松分布。
假如你把“连续的时间”分割成无数小份，那么每个小份之间都是相互独立的。在每个很小的时间区间内，电子元件都有可能“遭受到脉冲”或者“没有遭受到脉冲”，这就可以被认为是一个p很小的二项分布。而因为“连续的时间”被分割成无穷多份，因此n(试验次数)很大。所以，泊松分布可以认为是二项分布的一种极限形式。
因为二项分布其实就是一个最最简单的“发生”与“不发生”的分布，它可以描述非常多的随机的自然界现象，因此其极限形式泊松分布自然也是非常有用的。