相关文章
概率论的学习和整理9:超几何分布 (未完成!!!)
目录
1超几何分布 Hypergeometric distribution
1.1 超几何分布的定义
1.2 为什么叫超几何分布
1.3 超几何分布的公式 (2种公式)
1.3.1 超几何分布的公式1 (总体型公式)
1.3.2 超几何分布的公式2 (拆…
概率论与数理统计基础(二):常用离散分布 二项、泊松、超几何分、几何、 负二项分布
本文列举了常见的离散分布,关于它们的背景、概率分布列、数学期望与方差,以及与之相关的一些重要性质;比如几何分布的无记忆性、 二项分布的泊松近似、超几何分布的二项近似。。。。可作为离散分布的知识速查表。
目录
1. 二项分布b(n,p)
…
如何理解几何分布与指数分布的无记忆性?
在经济学上,有一个概念是沉没成本,大概指的是已经付出的、且不可收回的成本。针对这个概念有一个常见的说法: 这句话的意思是,既然沉没成本不可收回,那么在做选择的时候就不应该考虑它。举一个简单的例子,买…
统计学:几何分布、二项分布、泊松分布
一、几何分布
假设某种赌博游戏的胜率为0.2,那么意味着你玩第一次就胜出的概率为0.2。
那玩第二次才胜出呢?“玩第二次才胜出”就意味着玩第一次是失败的,而直到第二次才胜出,那么这件事发生的概率就是0.80.20.16。
那么第三次…
统计学 分布篇 - Hypergeometric Distribution(超几何分布)
超几何分布: 是 离散随机分布的一种. 它描述的是 从 n 中 拿 k 个成功的事件的概率( 不放回, 不放回意味着该事件是非独立事件), 其中在 N 中一共有 K 个成功事件.
n 为 样本数量, k 为样本中成功的概率
N为 事件的总数量(population), K为 在N中 事件的总数量. note: 超几…
几何分布的期望与方差
几何分布的期望与方差 高中数学教科书新版第三册(选修II)比原来的修订本新增加随机变量的几何分布,但书中只给出了结论:(1),(2),而未加以证明。本文给出证明&…
概率统计14——几何分布
我家小朋友年方1岁半,家里每天上午都要出去遛小孩。现在小朋友有两项爱好,在家翻垃圾桶,出门捡烟头。 翻垃圾桶可以有效地限制,捡烟头可是防不胜防。 也许烟头能散发出特殊的能量波动,小区的绿化带和草坪上的大部分烟…
几何分布和二项分布有什么区别?
● 每周一言
越长大越渺小。
导语
各种常见的分布中,二项分布和几何分布经常同时出现,在前面讲泊松分布的时候也简单提到了二项分布。那么,几何分布是什么分布?和二项分布有什么区别?
几何分布
讲泊松分布的时候提…
几何分布GeometricDistribution
几何分布
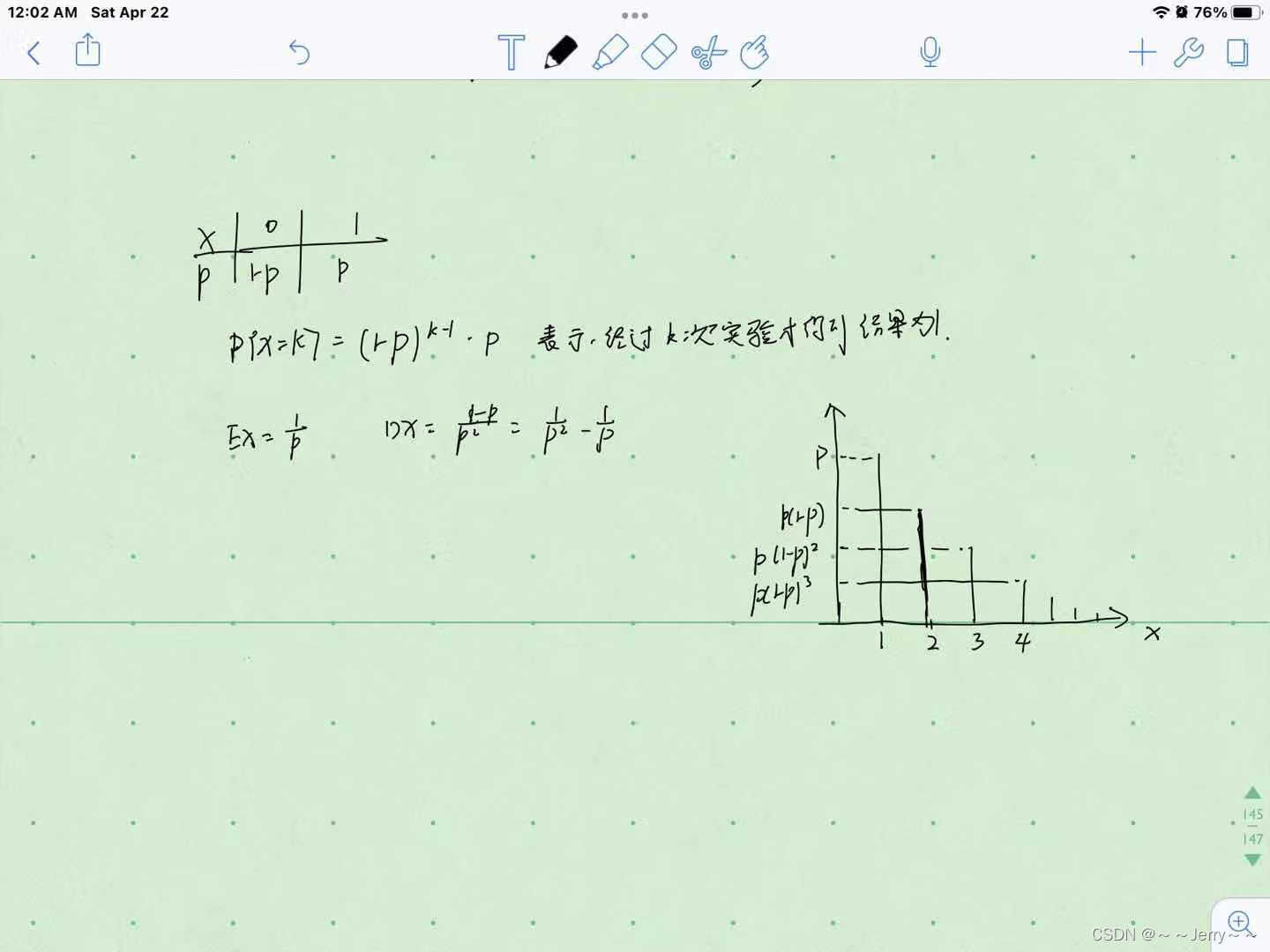
几何分布用于描述这种分布:独立事件的结果只有2个:”1和0“ 或”成功和失败“等,成功的概率为 p p p, 失败的概率为 q 1 − p q1-p q1−p; 第r次成功的概率为 P ( X r ) p ⋅ q r − 1 P(Xr)p\cdot q^{r-1} P(Xr)p⋅qr−1
即用…
MCS:离散随机变量——几何分布
Geometric
几何分布(Geometric distribution)是离散型概率分布。其中一种定义为:在 n n n次伯努利试验中,试验 k k k次才得到第一次成功的机率。详细地说,是:前 k − 1 k-1 k−1次皆失败,第 k …
概率论的学习和整理8: 几何分布
目录
前言
1 什么是几何分布
1.1 常规定义
1.2 另外一种定义
2 几何分布在概率分布中的定位
3 几何分布的 概率,期望,方差
4 为什么叫几何分布 (几何等比)
4.1 先需要了解算术平均数和几何平均数
4.2 第1:几…
几何分布(一种离散分布)
几何分布 几何分布是伯努利分布的推广,不断重复伯努利试验,直到首次成功为止,随机变量 X X X表示首次成功时已经完成的试验次数,我们称 X X X 是一个服从几何分布的随机变量 适用情况举例 实际中有不少随机变量服从几何分布&…
离散型概率分布之二——几何分布
上一篇博客讲了一下二项分布,这一篇打算讲一下几何分布。
其实,几何分布跟二项分布极为相似,至于相似到了什么地步,话不多说,往下看您就知道了。
由于是同系列的博客,所以用同样的思路来讲。 首先&#x…
视频教程-清华-尹成老师-Python爬虫day48-Python
清华-尹成老师-Python爬虫day48 毕业于清华大学,曾担任Google算法工程师,微软人工智能领域全球最具价值专家,微软Tech Ed 大会金牌讲师。 精通C/ C,Python ,Go语言,Sicikit-Learn与TensorFlow拥有15年编程经验与5年的教学经验&…
视频教程-清华-尹成老师-java基础-Day21-Java
清华-尹成老师-java基础-Day21 毕业于清华大学,曾担任Google算法工程师,微软人工智能领域全球最具价值专家,微软Tech Ed 大会金牌讲师。 精通C/ C,Python ,Go语言,Sicikit-Learn与TensorFlow拥有15年编程经验与5年的教学经验&…
视频教程-清华-尹成老师-Python开发环境-web-Python
清华-尹成老师-Python开发环境-web 毕业于清华大学,曾担任Google算法工程师,微软人工智能领域全球最具价值专家,微软Tech Ed 大会金牌讲师。 精通C/ C,Python ,Go语言,Sicikit-Learn与TensorFlow拥有15年编程经验与5年的教学经验&…
视频教程-清华-尹成老师-java基础-Day18-Java
清华-尹成老师-java基础-Day18 毕业于清华大学,曾担任Google算法工程师,微软人工智能领域全球最具价值专家,微软Tech Ed 大会金牌讲师。 精通C/ C,Python ,Go语言,Sicikit-Learn与TensorFlow拥有15年编程经验与5年的教学经验&…