计算方法实验一,方程求根
分别用Matlab和C写了一下,初学Matlab,如有不足还请指正。
实验内容:
1)在区间[0,1]内用二分法求方程 e x + 10 ∗ x − 2 e^x+10*x-2 ex+10∗x−2的近似根,要求误差不超过 0.5 × 1 0 − 3 0.5\times10^{-3} 0.5×10−3。
2)取初值 x 0 = 0 x_0=0 x0=0,用迭代公式 x k + 1 = 2 − e x k 10 , ( k = 0 , 1 , 2 , . . . ) x_{k+1}=\frac{2-e^{x_k}}{10},(k=0,1,2,...) xk+1=102−exk,(k=0,1,2,...)求方程 e x + 10 ∗ x − 2 e^x+10*x-2 ex+10∗x−2的近似根,要求误差不超过 0.5 × 1 0 − 3 0.5\times10^{-3} 0.5×10−3。
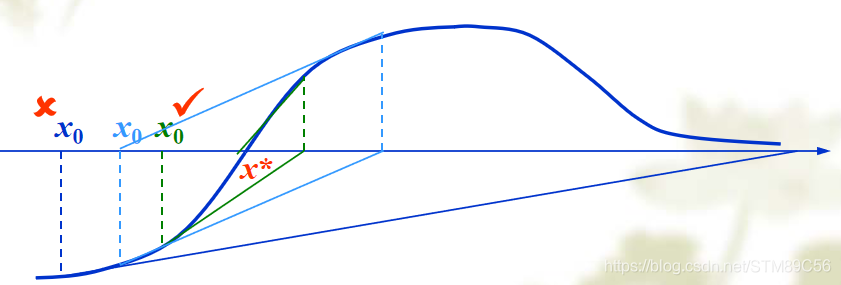
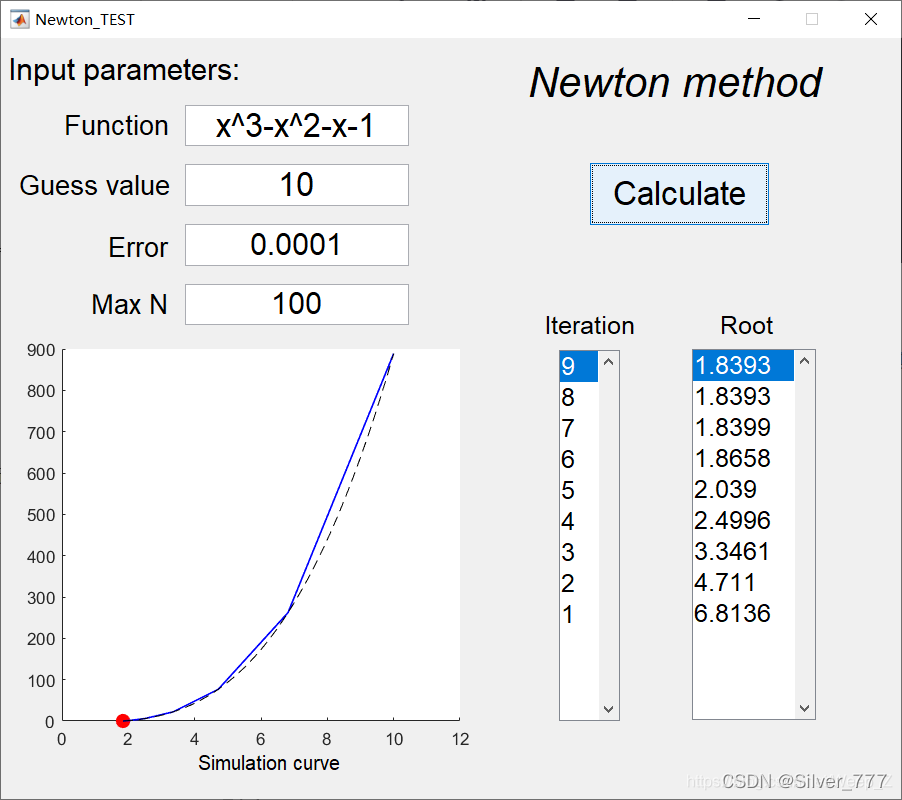
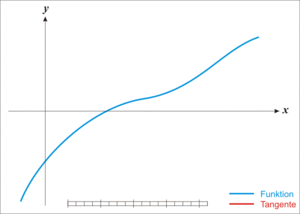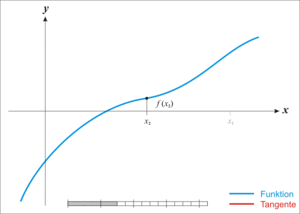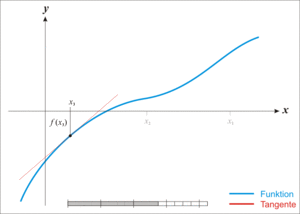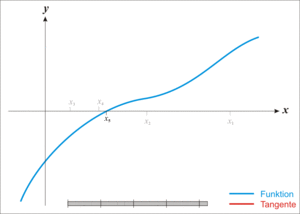
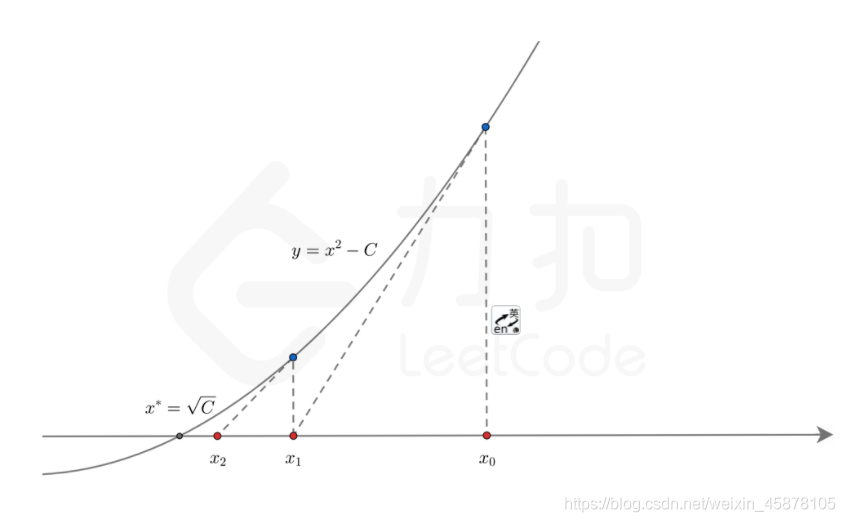
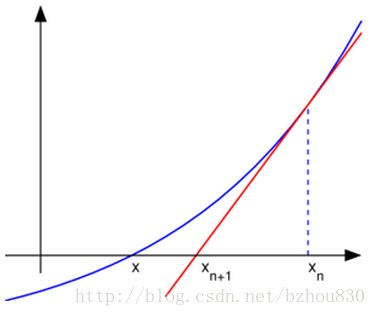
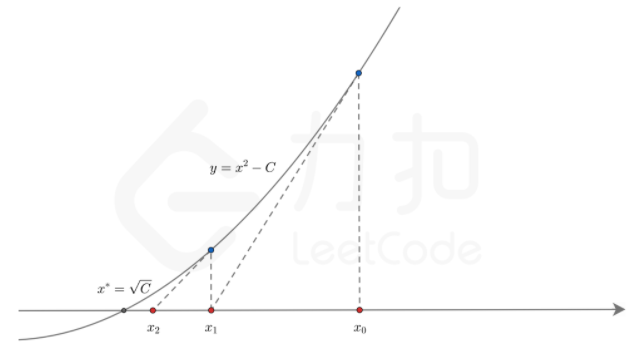
3)取初值 x 0 = 0 x_0=0 x0=0,用牛顿迭代法求方程 e x + 10 ∗ x − 2 e^x+10*x-2 ex+10∗x−2的近似根,要求误差不超过 0.5 × 1 0 − 3 0.5\times10^{-3} 0.5×10−3。
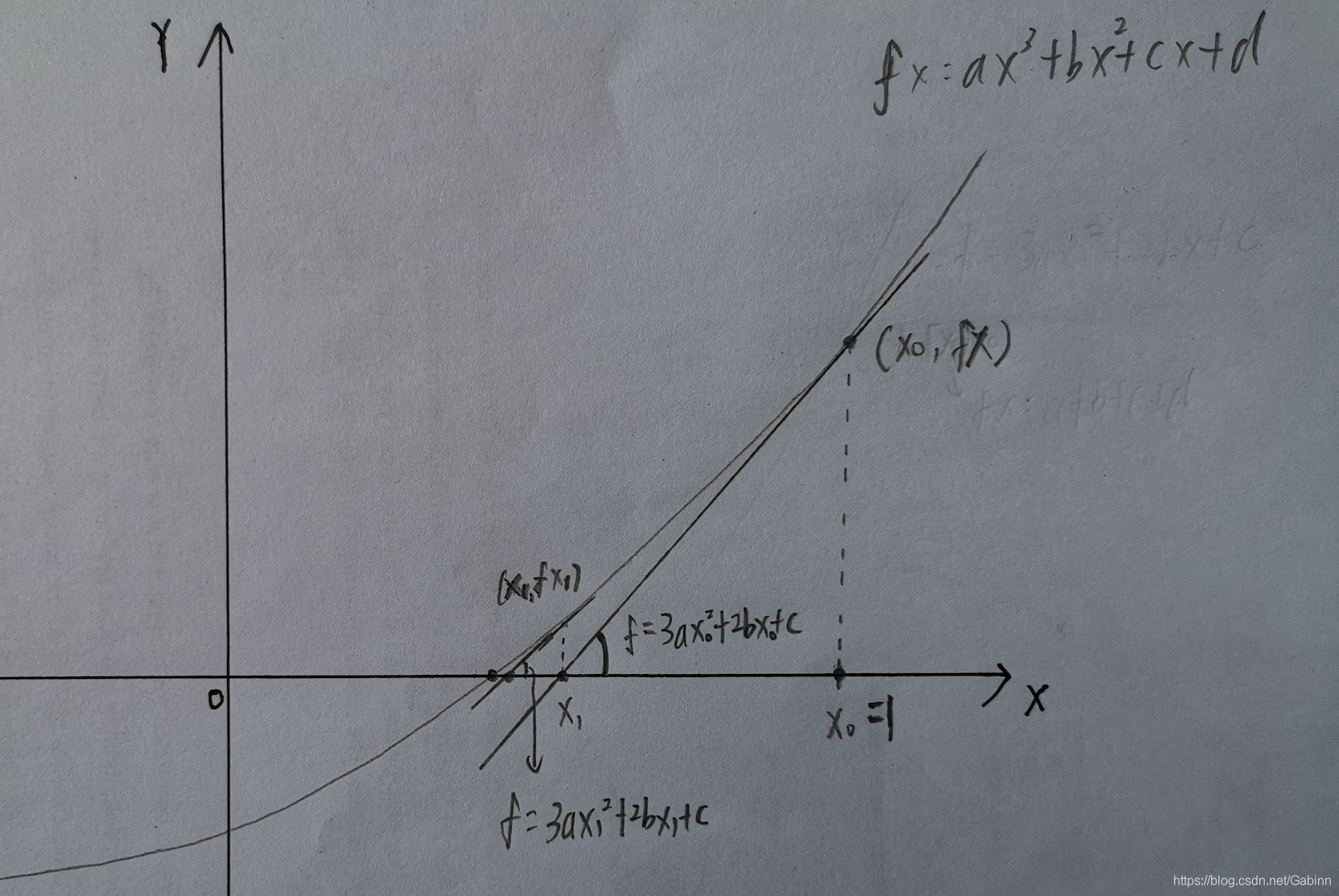
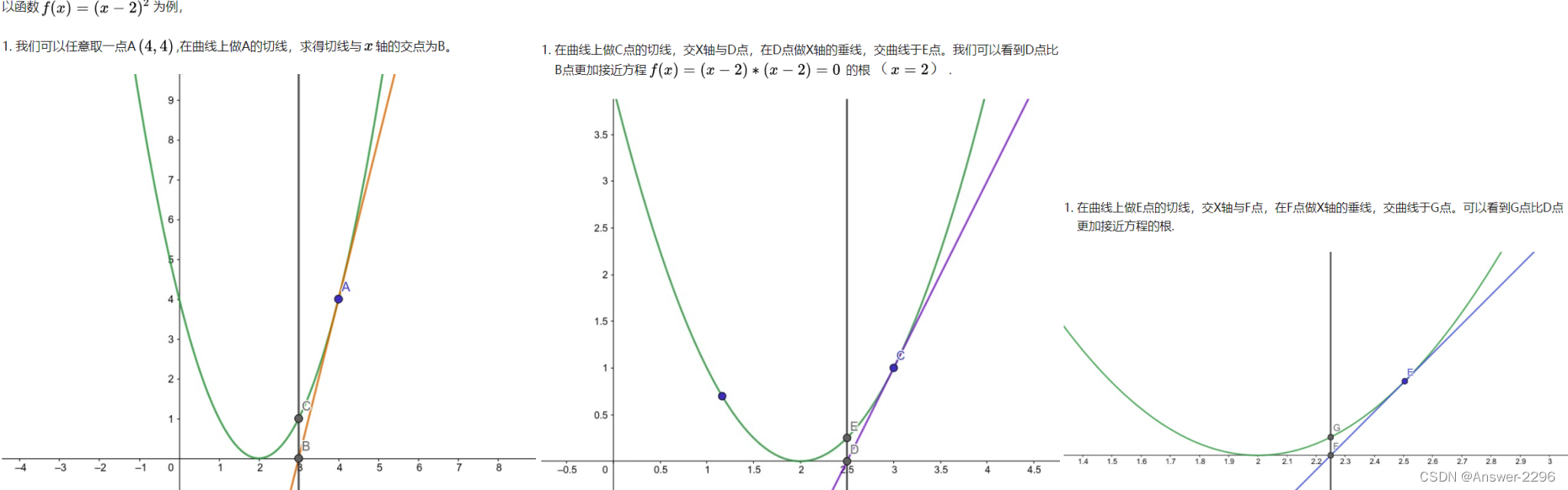
牛顿迭代公式: x k + 1 = x k − f ( x k ) f ′ ( x k ) x_{k+1}=x_k-\frac{f(x_k)}{f'(x_k)} xk+1=xk−f′(xk)f(xk)。
1. C
#include <stdio.h>
#include <Windows.h>
#include <math.h>#define WUCHA (0.5*pow(10, -4))double f_x(double x);
double erfenfa();
double diedai();
double newtown();int cnt = 0;int main()
{// 二分法printf("二分法:%lf\n", erfenfa());printf("计算次数%d\n", cnt);// 迭代法printf("迭代法:%lf\n", diedai());printf("计算次数%d\n", cnt);// 牛顿法printf("牛顿法:%lf\n", newtown());printf("计算次数%d\n", cnt);system("pause");return 0;
}// f(x)
double f_x(double x)
{return (exp(x) + 10 * x - 2);
}// f'(x)
double fd_x(double x)
{return (exp(x) + 10);
}// 牛顿法
double newtown()
{cnt = 0;double x0 = 0.0;double ret = f_x(x0);double xk = x0 - f_x(x0) / fd_x(x0);for (int k = 0; ; k++){cnt++;if (fabs(ret - 0) <= WUCHA){break;}xk = xk - f_x(xk) / fd_x(xk);ret = f_x(xk);}return xk;
}// 迭代法
double diedai()
{cnt = 0;double x0 = 0.0;double ret = f_x(x0);double xk = x0;//int k = 0;for (int k = 0; ; k++){cnt++;if (fabs(ret - 0) <= WUCHA){break;}xk = ((2 - exp(xk)) / 10);ret = f_x(xk);}return xk;
}// 二分法
double erfenfa()
{cnt = 0;double left = 0.0;double right = 0.1;double x = (left + right) / 2;double ret = f_x(x);while (fabs(ret - 0) >= WUCHA){cnt++;if (ret > 0){right = x;}if (ret < 0){left = x;}x = (left + right) / 2;ret = f_x(x);}return x;
}
分界线
2. Matlab
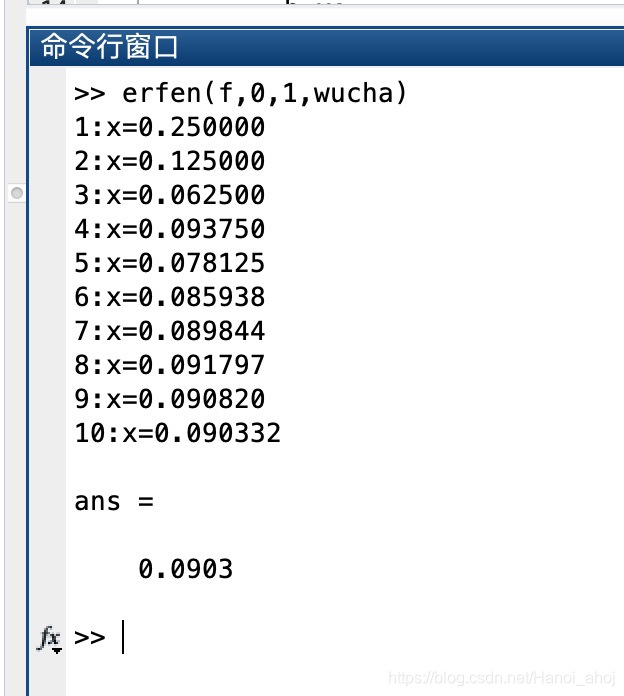
2.1 二分法
function x = erfen(f,a,b,e)
% f是函数名 a,b是区间端点,e为精度
fa = feval(f,a); % feval是求函数值
fb = feval(f,b);
if fa*fb>0error('此函数在[%d,%d]区间无解',a,b);
endk = 0;
x = (a+b)/2;
while(b-a)>(2*e)fx=feval(f,x);if fa*fx<0b=x;fb=fx;elsea=x;fb=fx;endk=k+1;x=(a+b)/2;fprintf("%d:x=%f\n", k, x);end
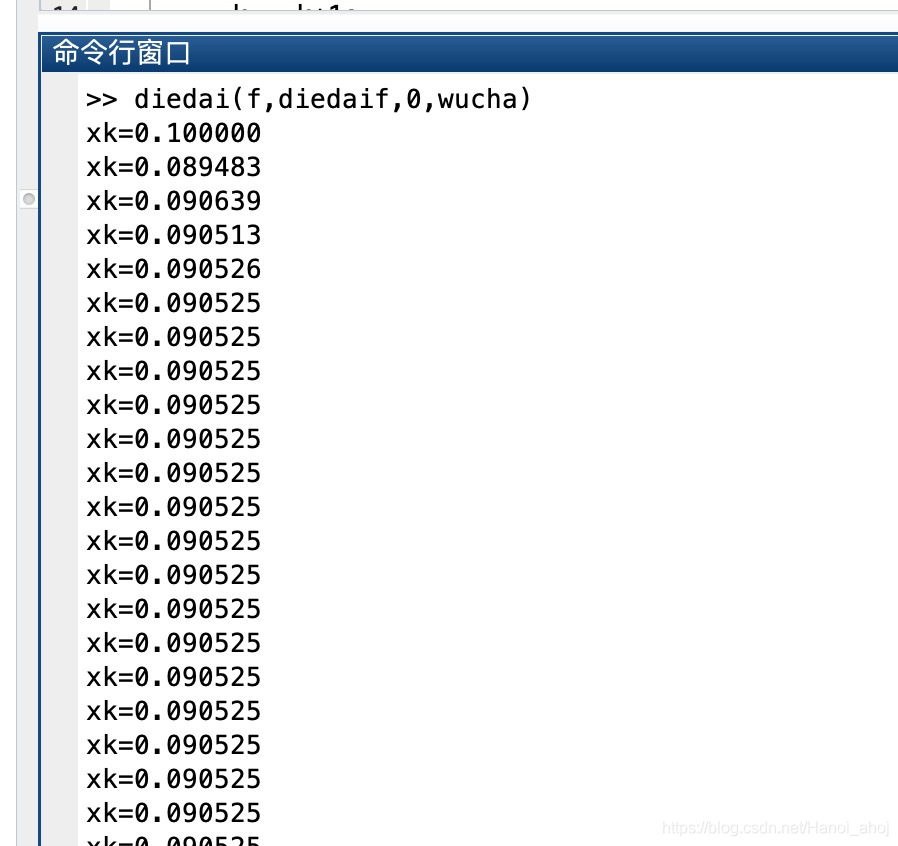
2.2 不动点迭代法
function x = diedai(f,diedaif,x0,e)N = 10; %最大迭代次数ret = feval(diedaif,x0);
xk = x0;
k = 0;while abs(x0-ret)>e & k<Nxk = feval(diedaif,xk);ret = feval(diedaif,xk);k = k+1;fprintf("xk=%f\n", xk);%if% break;%endendif k==Nfprintf('超过最大迭代次数限制\n');end
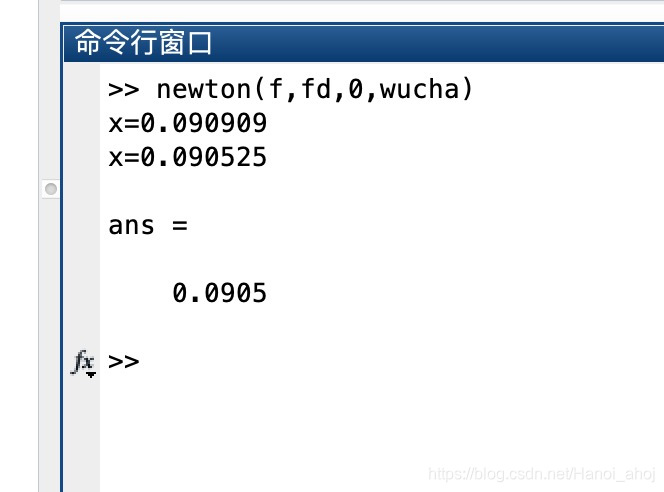
2.3 牛顿法
function x = newton(f,fd,x0,e)
% f->f(x)
% fd->f'(x)
% x0=0
% e=0.0005N = 100; %最大迭代次数100
x = x0;
x0 = x+2*e;
k = 0;
while abs(x0-x)>e & k<Nk = k+1;x0=x;x=x0-feval(f,x0)/feval(fd,x0);fprintf("x=%f\n", x);
endif k==Nwarning('超过最大迭代次数限制');end
分界线
3.实验结果
3.1 C
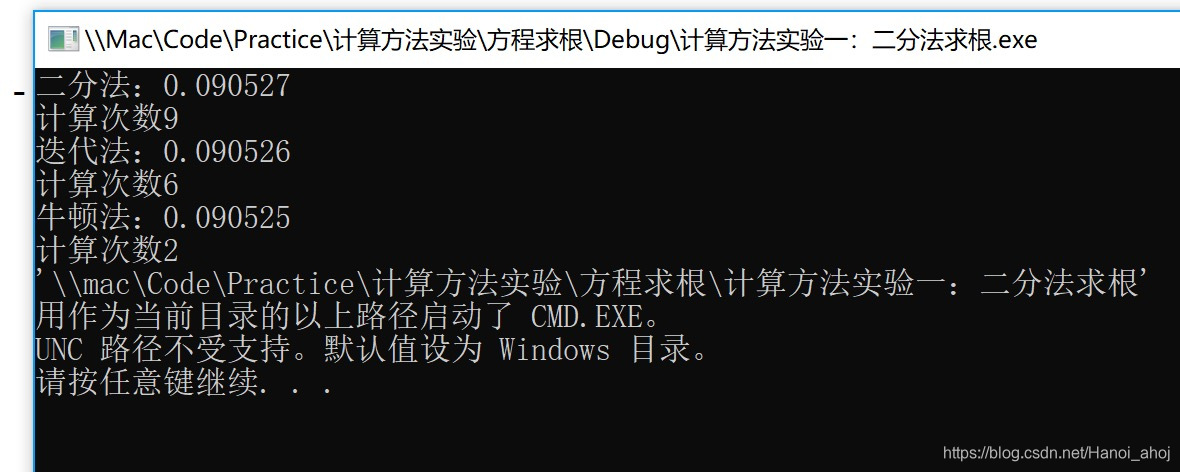
3.2 Matlab