1. 问题描述

编写用牛顿迭代法求方程根的函数。

方程为 $ax^2+bx^2+cx+d=0$ ，系数a，b，c，d 由主函数输入。

求 $x$ 在 $1$ 附近的一个实根。求出根后，由主函数输出。

牛顿迭代法的公式是： $-\frac{f(x_0 )}{f'(x_0)}$ ，设迭代到 $|x-x_0|\leq10^{-5}$ 时结束。

2. 题目分析

牛顿迭代法是取 $x_0$ 之后，在这个基础上，找到比 $x_0$ 更接近的方程的根，一步一步迭代，从而找到更接近方程根的近似根。

设 $r$ 是 $f (x) = 0$ 的根，选取 $x_0$ 作为 $r$ 初始近似值。

过点 $x_0, f(x_0))$ 作为曲线 $y = f (x)$ 的切线 $L$ ，

$L$ 的方程为 $y=f(x_0)+f'(x_0)*(x-x_0)$ ，

求出 L 与 x 轴交点的横坐标 $x_1=x_0-f(x_0)/f'(x_0)$ ，称 $x$ 为 $r$ 的一次近似值，

过点 $x_1,f(x_1))$ 作为曲线 $y = f (x)$ 的切线，并求该切线与 x 轴的横坐标 $x_2=x_1-f(x_1)/f'(x_1)$ ，称 $x_2$ 为 $r$ 的二次近似值，

重复以上过程，得 $r$ 的近似值 $x_n$ 。

上述过程即为牛顿迭代法的求解过程。

3. 算法设计

程序流程分析👇

(1) 在 $1$ 附近找任一实数作为 $x_0$ 的初值，我们取 $1.5$ ，即 $x_0=1.5$

(2) 用初值 $x_0$ 代入方程中计算此时的 $f(x_0)$ 及 $f'(x_0)$ ；程序中用变量 $f$ 描述方程的值，用 $f d$ 描述方程求导之后的值。

(3) 计算增量 $h = f / f d$ 。

(4) 计算下一个 $x:x=x_0-h$ 。

(5) 用新产生的 $x$ 替换原来的 $x_o$ ，为下一次迭代做好准备。

(6) 若 $x-x_0|>=1e-5$ ，则转到第 (3) 步继续执行，否则转到步骤 (7)。

(7) 所求 $x$ 就是方程 $ax^3+bx^2+cx+d=0$ 的根，将其输出。

本程序的编写既可用 while，也可用 do...while，二者得到的结果是一样的，只是在赋初值时稍有不同。

while 结构需要先判定条件，即先判断 $x-x_0|>=1e-5$ 是否成立，这样对于 $x$ ， $x_0$ 我们要在 $1$ 附近取两个不同的数值作为初值；

do...while 结构是先执行一次循环体，得到 $x$ 的新值后再进行判定，这样程序开始只需给 $x$ 赋初值。

这里我们采用 do...while 结构来实现。

4. 确定程序框架

程序的主体结构如下👇

由于程序中用到了绝对值函数 fabs() ，所以在程序的开始要加上头文件#include <math.h>。

流程图如下所示👇

5. 迭代法求方程根

编写程序时要注意的一点是判定 $x-x_0|>=1e-5$ 。

从牛顿迭代法的原理可以看出：迭代的实质就是越来越接近方程根的精确值，最初给 $x_0$ 所赋初值与根的精确值是相差很多了，正是因为这个我们才需要不断地进行迭代，也就是程序中循环体的功能。

在经过一番迭代之后所求得的值之间的差别也越来越小，直到求得的某两个值的差的绝对值在某个范围之内时，便可结束迭代。

若我们把判定条件改为 $x-x_0|<1e-5$ ，则第一次的判断结果必为假，这样就不能进入循环体再次执行。

定义 solution()函数求方程的根。solution()函数的代码如下👇

6. 代码实现

完整代码📝

#include <stdio.h>
#include <math.h>float solution(float a, float b, float c, float d)
{float x0, f, fd, h; float x = 1.5;do{x0 = x; f = a * x0 * x0 * x0 + b * x0 * x0 + c * x0 + d;fd = 3 * a * x0 * x0 + 2 * b * x0 + c;h = f / fd;x = x0 - h; } while (fabs(x-x0) >= 1e-5);return x;
}int main()
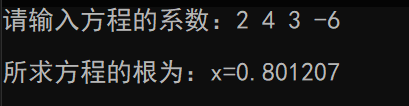
{float a, b, c, d; float x; printf("请输入方程的系数：");scanf("%f %f %f %f", &a, &b, &c, &d);x = solution(a, b, c, d);printf("\n");printf("所求方程的根为：x=%f\n", x);return 0;
}