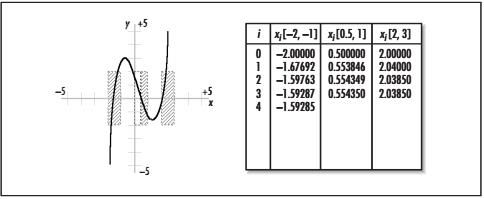
用牛顿迭代法求下面方程在1.5附近的根：2x³-4x²+3x+6=0

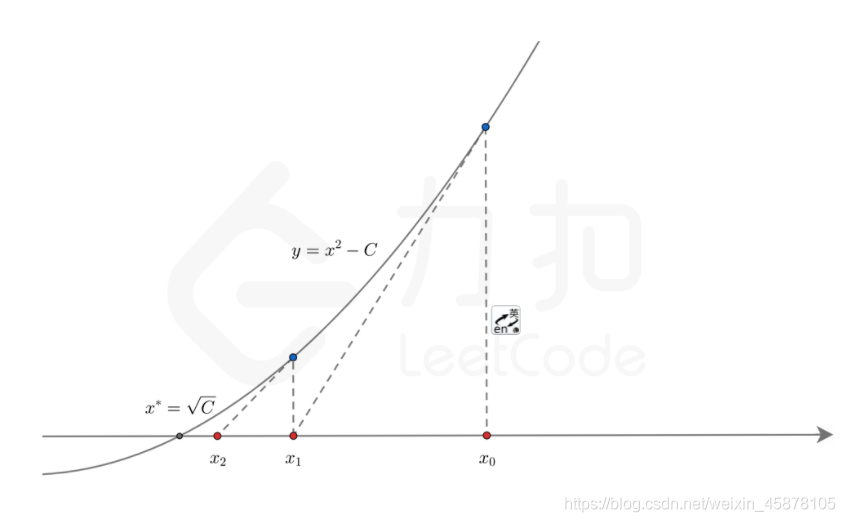
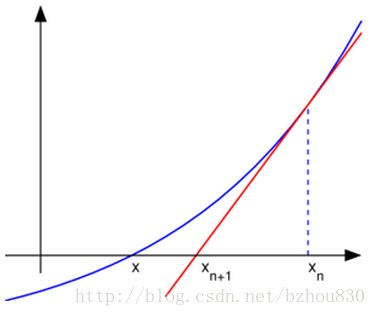
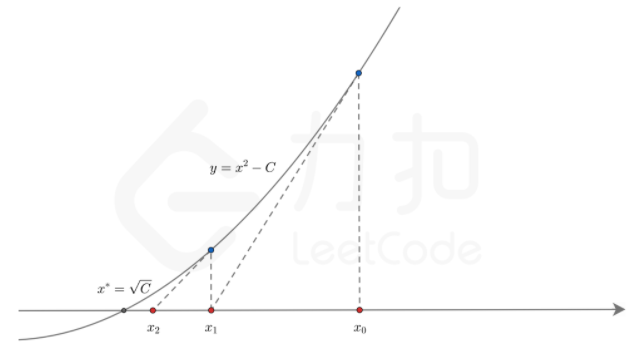
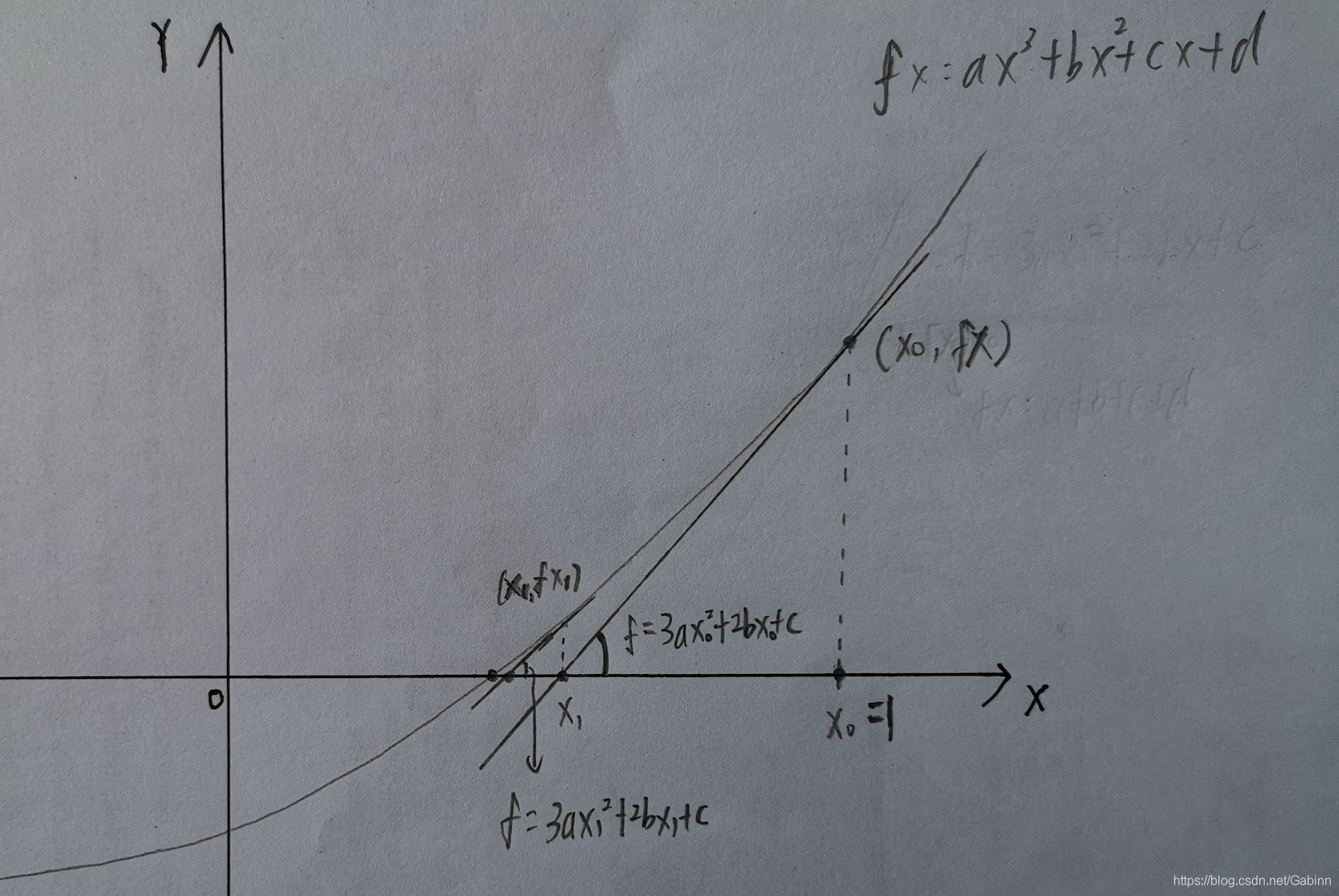
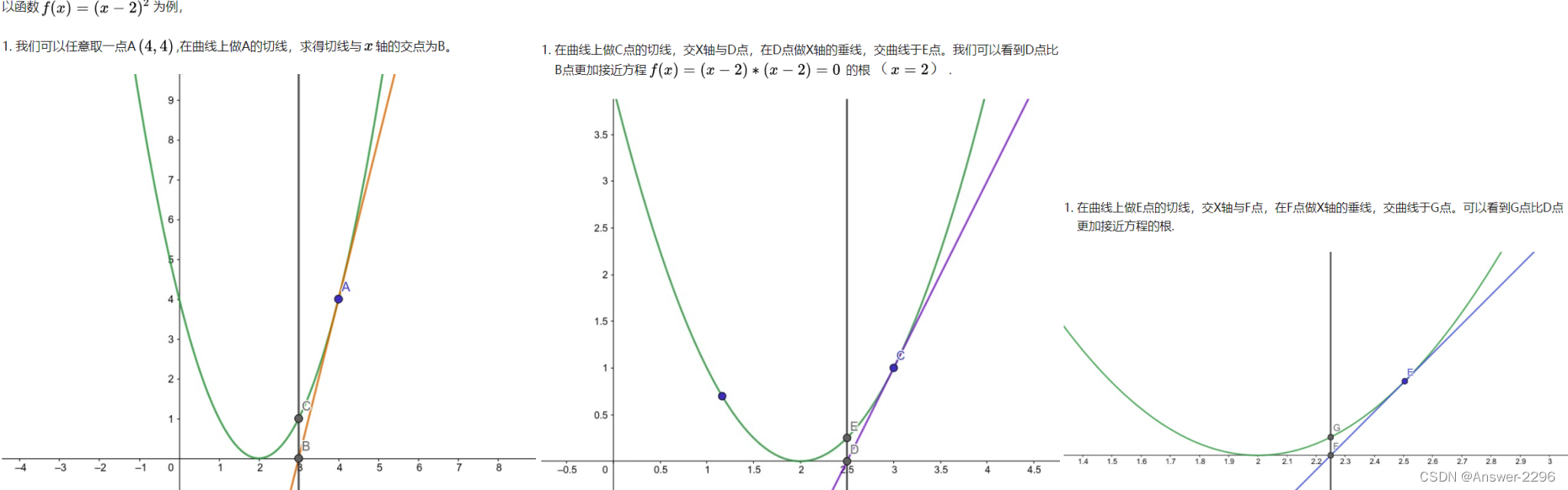
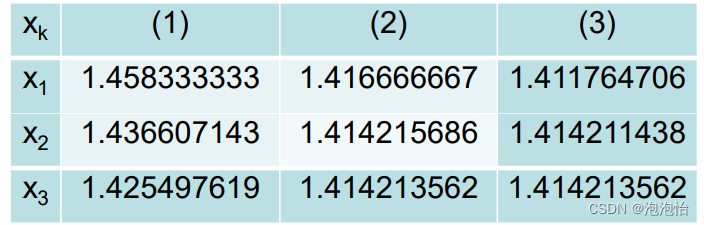
• 先定义一个x0,通过x0找出f(x0),做f(x0)的切线，切线的交点为x1，tanx=f(x0)/x1-x0;然而切线在函数中就是f(x)的导数，我们利用这一结论可以找出f(x0)和f(x0)的导数之间的关系，进而用到牛顿迭代，f^’(x0)=f(x0)/x1-x0,可求出x1=x0-f(x0)/f(x0)^'----牛顿迭代原理就推出来了。
• 把f(x)和f^’(x)关系求出，带入推导出来的公式，利用x0与x1之间的关系，即可就出结果。
• 代码如下：

#include<stdio.h>
#include<math.h>
int main()
{double x0,x1,f,f1;x1=1.5;while(fabs(x1-x0)>=1e-5){x0=x1;f=((2*x0-4)*x0+3)*x0-6;f1=(6*x0-8)*x0+3;x1=x0-f/f1;}printf("The root of equation is %5.2lf",x1);return 0;
}