说明：该篇博客源于博主的早些时候的一个csdn博客中的一篇，由于近期使用到了，所以再次作一总结。原文地址

概述

牛顿迭代法（Newton’s method）又称为牛顿-拉夫逊（拉弗森）方法（Newton-Raphson method），它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。

1. 牛顿迭代公式

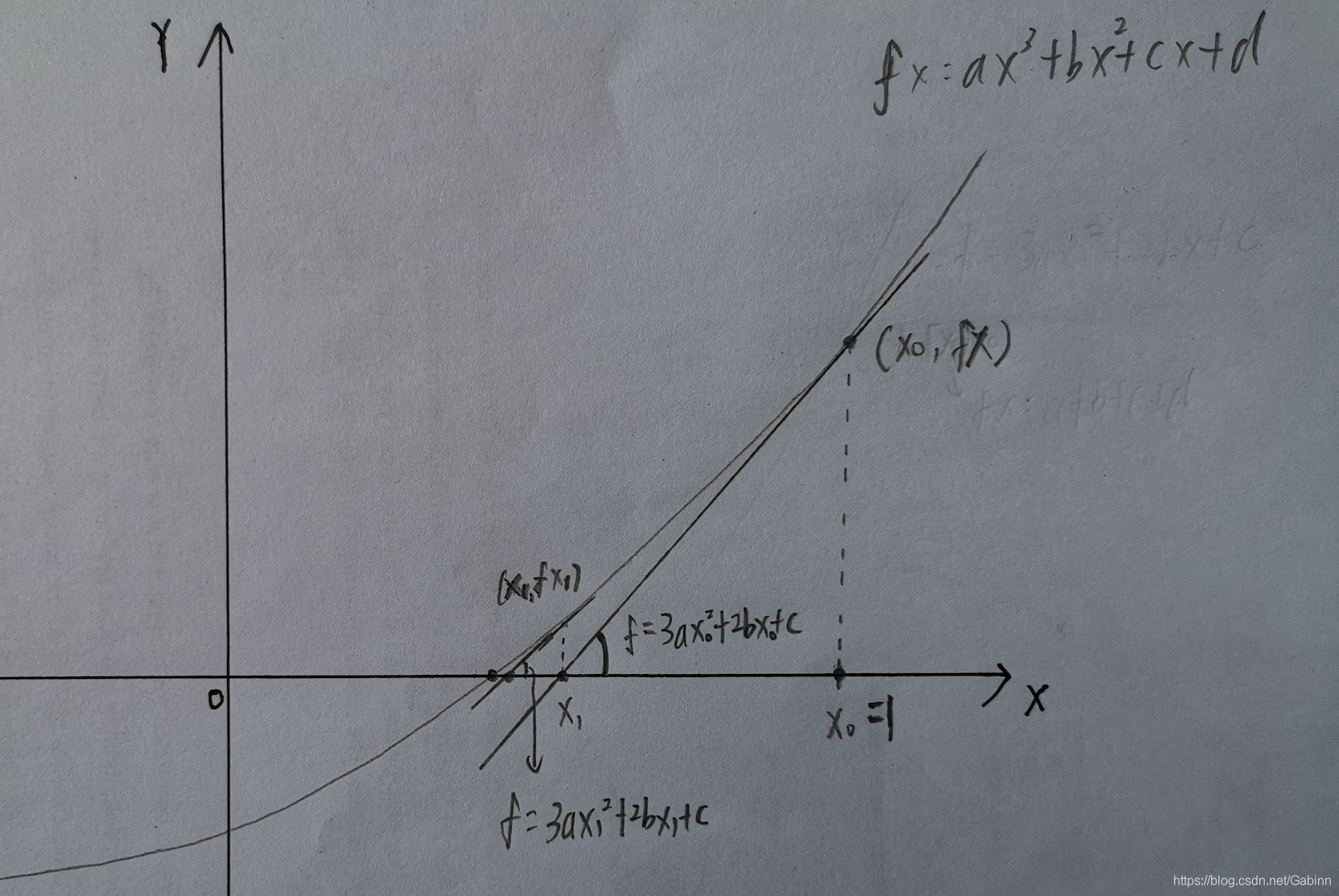
设$r$是 $f(x) = 0$ 的根，选取 $x_{0}$作为$r$的初始近似值，过点 $(x_{0}, f(x_{0})$ 做曲线$y = f(x)$的切线$L$，$L$的方程为 $y=f(x_{0}) + f^{'}(x_{0})(x-x_{0})$ ，求出$L$与$x$轴交点的横坐标 $x_{1} = x_{0} - \frac{f(x_{0})}{f^{'}(x_{0})}$，称$x_{1}$为$r$的一次近似值。
过点$(x_{1}, f(x_{1}))$做曲线 $y= f(x)$ 的切线，并求该切线与$x$轴交点的横坐标 $x_{2} = x_{1} - \frac{f(x_{1})}{f^{'}(x_{1})}$，称$x_{2}$为$r$的二次近似值。重复以上过程，得$r$的近似值序列，其中，$x_{n+1} = x_{n} - \frac{f(x_{n})}{f^{'}(x_{n})}$ 称为$r$的$n + 1$次近似值，上式称为牛顿迭代公式。

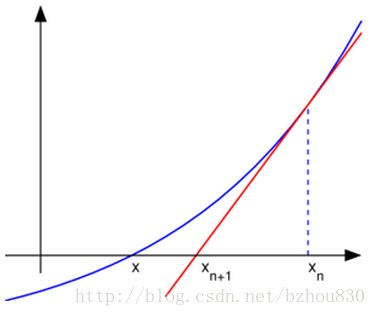
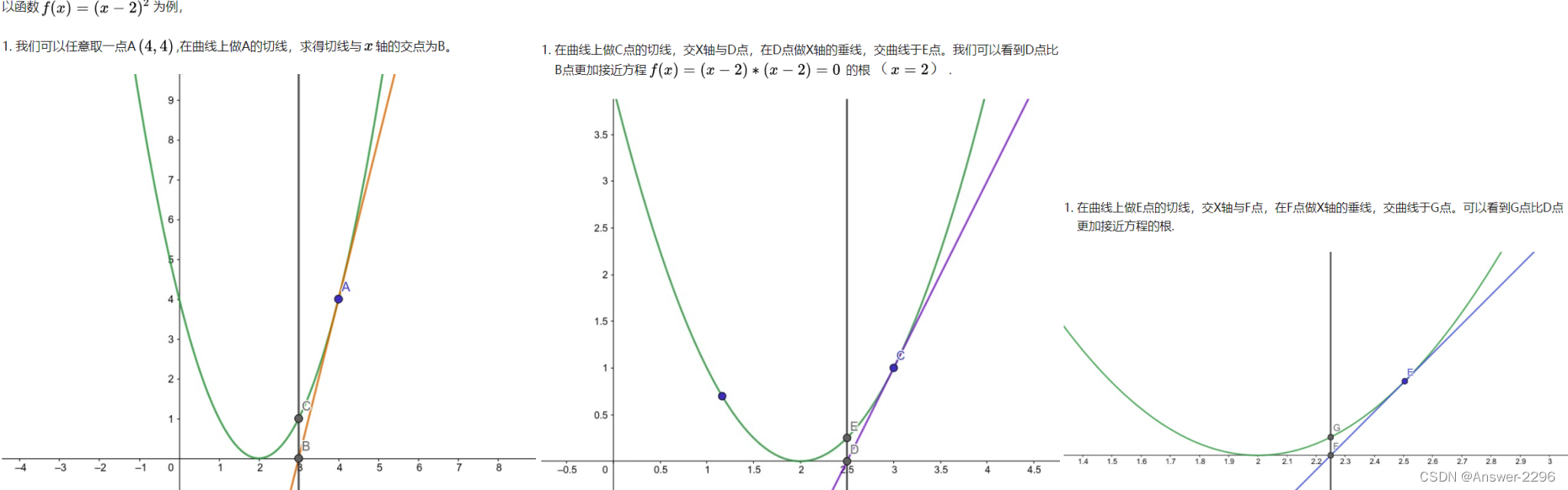
实际上牛顿迭代法就是将非线性的问题转化为线性问题再做处理。将非线性函数在小范围内用他的一阶泰勒级数表示（也就是在某点泰勒展开取低阶项）。

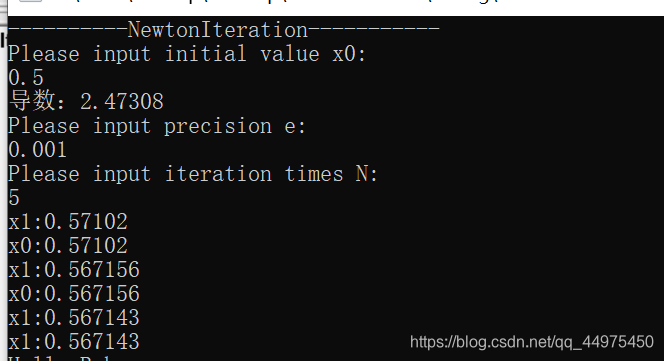
2. 使用牛顿迭代公式求解方程

求解步骤：
1. 原函数：$f(x) = x^{m} - a$
2. 原函数的导函数：$f^{'}(x) = mx^{m-1}$
3. 使用牛顿迭代公式$x_{n+1} = x_{n} - \frac{f(x_{n})}{f^{'}(x_{n})}$：

$$x_{n+1} = x_{n} - \frac{f(x_{n})}{f^{'}(x_{n})} = x_{n} - \frac{x^{m}_{n} - a }{mx^{m-1}_{n}}$$

3. 示例

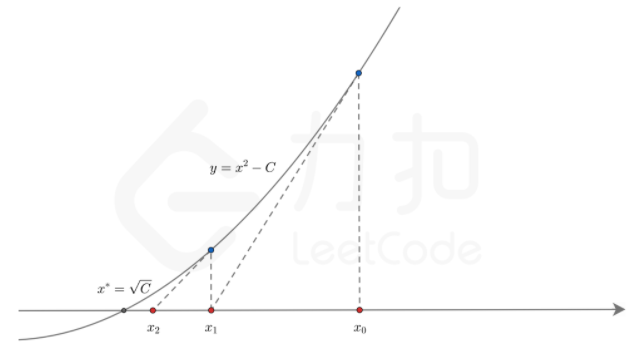
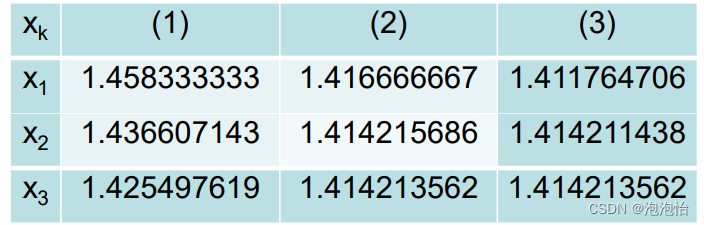
3.1 利用牛顿迭代公式求解平方根

求解平方根也就是求解函数$f(x) = x^{2} - a ，f(x) = 0$ 的根。根据上述的求解过程$f^{'}(x) = 2x$ ， 带入牛顿迭代公式：

$$x_{n+1} = x_{n} - \frac{x^{2}_{n} - a }{2x_{n}}$$

#include <iostream>
#include <math.h>using namespace std;int main()
{double m,x = 1.0;cout<<"Please Input a Num:"<<endl;cin>>m;if(m < 0){cout<<"Sorry,Input is Illegal"<<endl;}else if(m == 0){cout<<"0"<<endl;}else{while(fabs(m - (x*x)) >= 0.001){x = (x + m/x)/2.0;cout<<"x="<<x<<"\tm="<<m<<endl;      //显示运算过程}cout<<"The result is:"<<x<<endl;}system("pause");
}

3.2 另一种求解平方根的高效方法

提到这个算法就不得不说一个神奇的数字 0x5f375a86 。下面的代码来自于维基百科，关于更多该数字的奇闻可以点击下面的链接查看：
https://en.wikipedia.org/wiki/Fast_inverse_square_root

int sqrt(float x) 
{ if(x == 0) return 0; float result = x; float xhalf = 0.5f*result; int i = *(int*)&result; i = 0x5f375a86- (i>>1); result = *(float*)&i; result = result*(1.5f-xhalf*result*result); // Newton step, repeating increases accuracy result = result*(1.5f-xhalf*result*result); return 1.0f/result; 
}