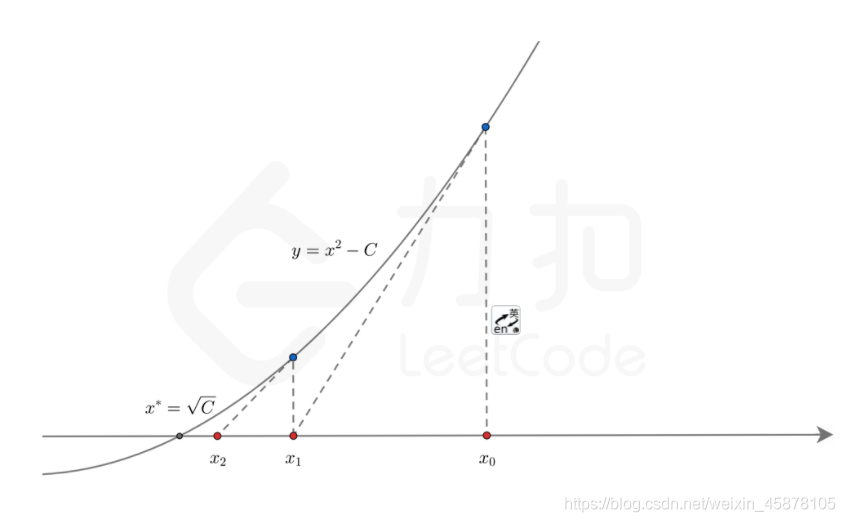
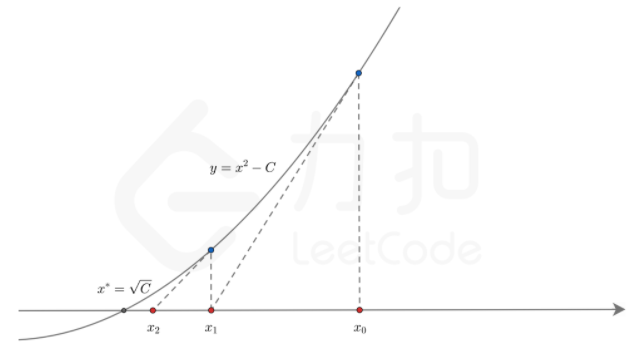
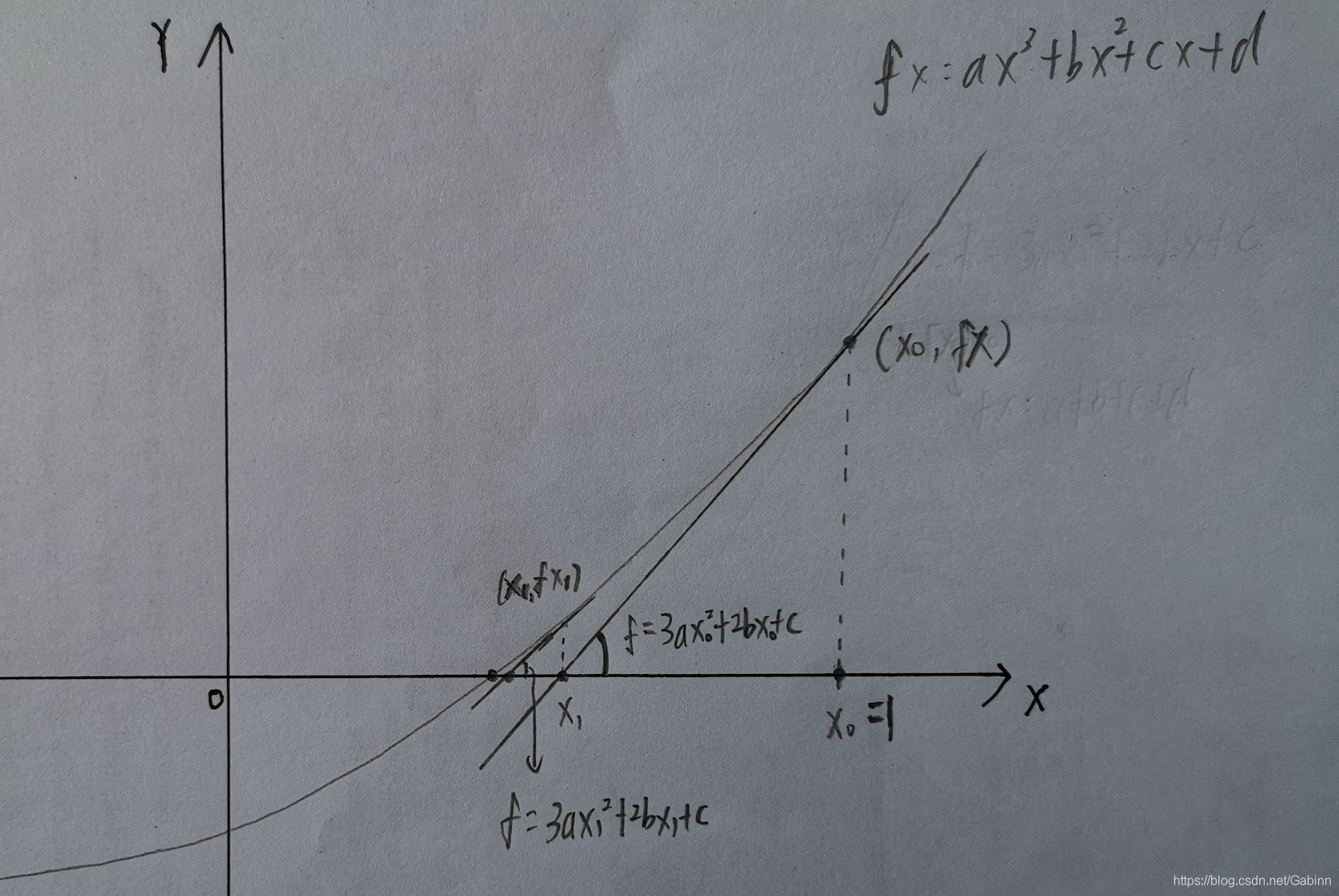
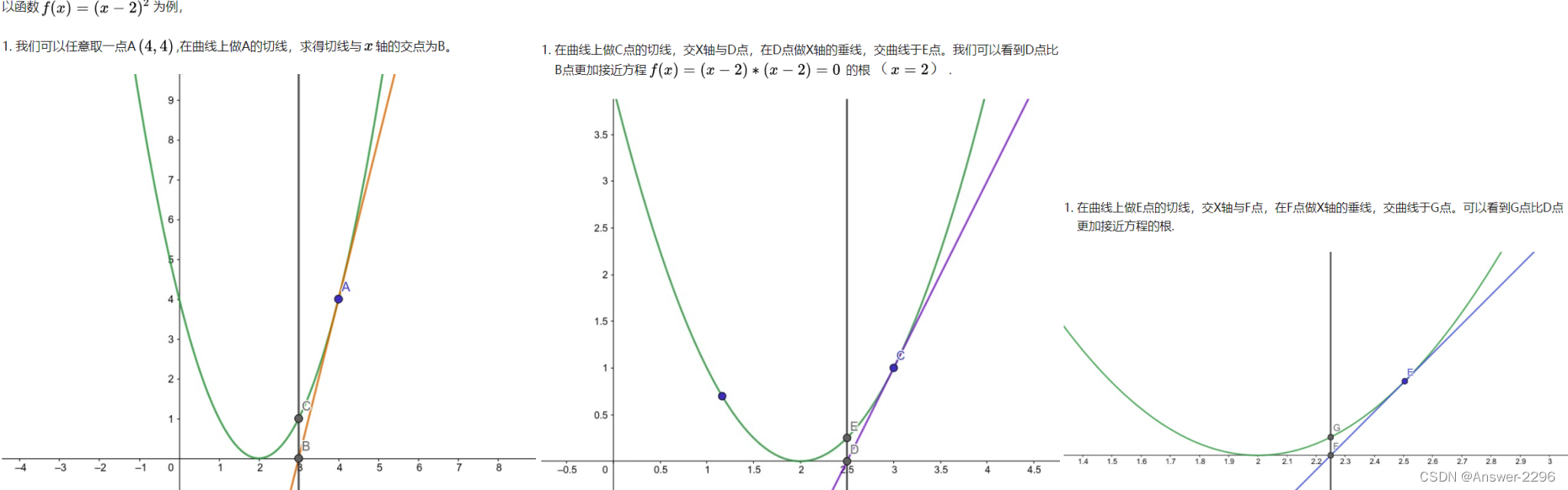
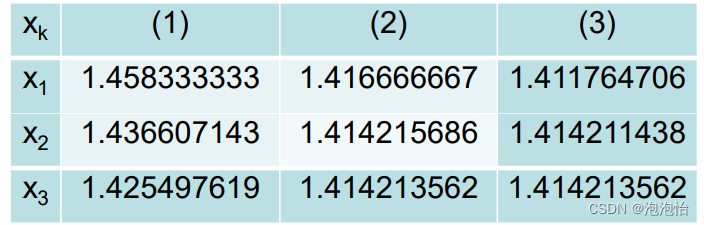
题目：牛顿迭代法

程序1：牛顿迭代法通用函数

function [x] = newton(x0,epsilon,f,print_flag)
digits(10)  % 控制牛顿迭代法的运算精度，精度太大迭代速度过慢
syms x
f(x) = f;
df(x) = diff(f);
count = 0;
e = 1;while abs(e) > epsilonx1 = vpa(x0 - f(x0)/df(x0));e = vpa(x1 -x0);x0 = x1;count = count + 1;if count>100fprintf('牛顿迭代发散。\n')breakendif print_flagfprintf('已迭代 %d 次,', count)fprintf('x为：%f,', x0)fprintf('误差为：%f\n', e)endendif print_flagfprintf('Newton迭代的近似解 x = %f\n',x1)fprintf('迭代次数count = %d\n',count)end
x = x0;
end

程序2：求最大Delta

clc;clear;close all%% 定义方程
syms x
f(x) = x^3 / 3 - x%% 寻找delta范围
delta = 0;             % delta的绝对值：|delta|
step = 0.1;            % delta递增的步长，初始步长为0.1
epsilon = 10^(-6);     % 允许的误差
while step > 10^(-7)a = 0; b = 0;while abs(a) < epsilon & abs(b) < epsilona = newton(delta,epsilon,f,0);b = newton(-delta,epsilon,f,0);delta = delta + step;end% 当牛顿迭代发散时，修改步长大小delta = delta - 2 * step;step = step * 0.1;delta = delta + step;stepfprintf('delta:%f\n', delta)
end
fprintf('Newton迭代序列收敛于根x2时, delta应小于：%f\n',delta)

程序3：观察结果

clc;clear;close all%% 定义方程
syms x
f(x) = x^3 / 3 - x%% 寻找delta范围
delta = 0;             % delta的绝对值：|delta|
step = 0.1;            % delta递增的步长，初始步长为0.1
epsilon = 10^(-6);     % 允许的误差%% A
x0 = -200;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)x0 = -50;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)x0 = -2;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)x0 = -1.1;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)
fprintf('\n')%% B
x0 = -0.9;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)x0 = -0.85;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)x0 = -0.8;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)x0 = -0.78;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)
fprintf('\n')
%% D
x0 = 0.78;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)x0 = 0.8;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)x0 = 0.85;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)x0 = 0.9;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)
fprintf('\n')
%% E
x0 = 1.1;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)x0 = 2;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)x0 = 50;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)x0 = 200;
x = newton(x0,epsilon,f,0);
fprintf('x0 = %f\n',x0)
fprintf('迭代结果x = %f\n',x)