迭代法的作用

许多复杂的求解问题，都可以转换成方程f(x)=0的求解问题。这一系列的解叫做方程的根。对于非线性方程的求解，在自变量范围内往往有多个解，我们将此变化区域分为多个小的子区间，对每个区间进行分别求解。我们在求解过程中，选取一个近似值或者近似区间，然后运用迭代方法逐步逼近真实解。
方程求根的常用迭代法有：二分法、不动点迭代、牛顿法、弦截法。

牛顿迭代法

牛顿迭代法（Newton’s method）又称为牛顿-拉弗森方法（Newton-Raphson method），它是一种在实数域和复数域上近似求解方程的方法。方法使用函数的泰勒级数的前面几项来寻找方程的根。

参考链接：
用python算微积分及牛顿迭代求解高阶方程

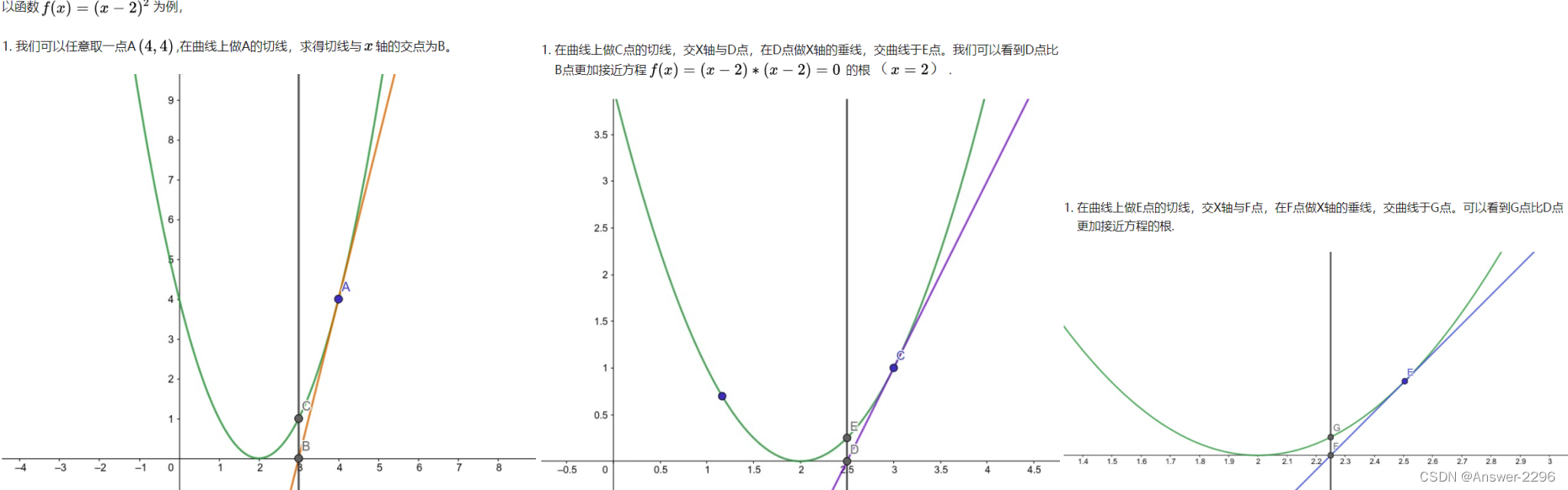
牛顿迭代法基本思想

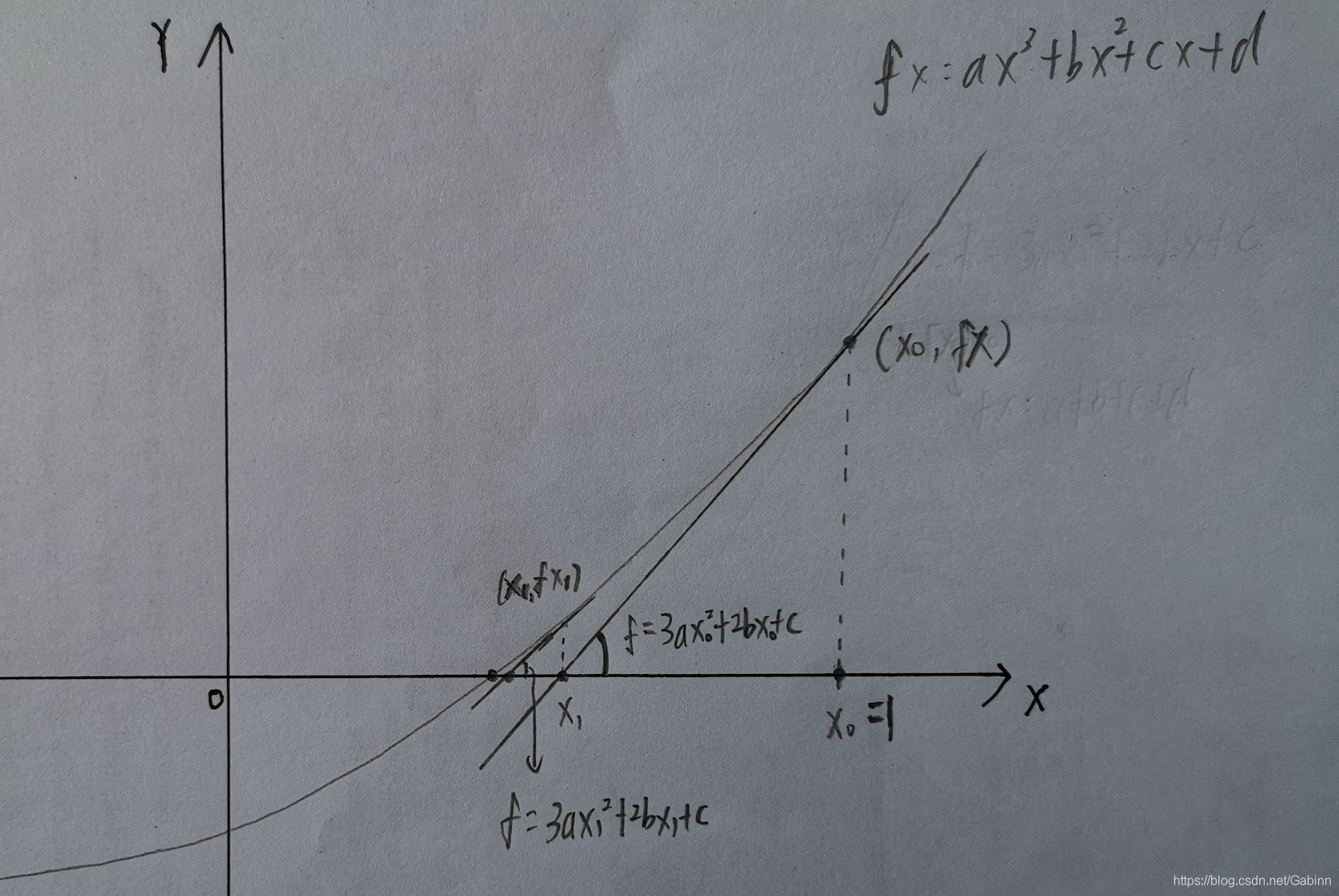
考察一般形式的函数方程f(x)=0,首先运用校正技术建立迭代公式，设已知它的近似根xk,则自然要求校正值x(k+1)=xk+∆x能更好的满足所给方程,即 f(xk+∆x)≈0，将其左端用线性主部f(xk)+f’(xk)* ∆x代替,而令f(xk)+f’(xk)*∆x=0，这是关于增量∆x的线性方程，据此定出∆x=-f(xk)/f’(xk)，从而关于校正值x(k+1)=xk+∆x有如下计算公式：X(k+1)=xk-f(xk)/f’(xk)

这就是著名的牛顿公式。Newton法的突出优点是速度快，但它有个明显的缺点是每一步迭代需要提供导数值f’(xk),如果函数f(x)比较复杂，致使导数的计算比较困难，那么使用牛顿公式是不方便的。

牛顿迭代法优缺点

通常最高效的方法：牛顿法。它是求解方程f(x)=0的一种重要方法，它的最大优点是方程在单根附近具有较高的收敛速度，且算法逻辑简单。它还可以用于求代数方程的重根、复根。但是由于牛顿法是局部收敛的，它的收敛性依赖于初值x0的选取。并且每一步迭代除了需要计算f(Xk)外，还需要计算f(Xk)的导数，当f(x)比较复杂时（缺点明显），该方法是不方便的。

例题

求方程式：x = exp(-x)在0.5附近的根
即求方程式xexp(x)-1=0在0.5附近的根

约定一个误差，当误差小于某个数值的时候，迭代停止

代码如下：

from sympy import *
x = symbols('x')
x0 = 0.5
x_list = [x0]
i = 0def f(x):f = x * exp(x) - 1return fwhile True:   if diff(f(x),x).subs(x,x0) == 0:print('极值点：',x0)breakelse:x0 = x0 - f(x0)/diff(f(x),x).subs(x,x0)x_list.append(x0)if len(x_list) > 1:i += 1error = abs((x_list[-1] - x_list[-2]) / x_list[-1])if error < 10 ** (-6):print(f'迭代第{i}次后，误差小于10^(-6)，误差为{error}')breakelse:pass
print(f'所求方程式的根为{x_list[-1]}')

结果：

迭代第4次后，误差小于10^(-6)，误差为2.17717477197250E-10
所求方程式的根为0.567143290409784

迭代至电脑默认为误差为0为止

from sympy import *x = symbols('x')
x0 = 0.5
x_list = [x0]
i = 0def f(x):f = x * exp(x) - 1return fwhile True:if diff(f(x),x).subs(x,x0) == 0:print('极值点：',x0)breakelse:x0 = x0 - f(x0)/diff(f(x),x).subs(x,x0)x_list.append(x0)if len(x_list) > 1:i += 1error = abs((x_list[-1] - x_list[-2]) / x_list[-1])if error == 0:print(f'迭代第{i}次后，误差为0')breakelse:passprint(f'所求方程式的根为{x_list[-1]}')

结果：

迭代第6次后，误差为0
所求方程式的根为0.567143290409784

画迭代图

代码：

from sympy import *
import matplotlib.pyplot as plt
x = symbols('x')
x0 = 0.5
x_list = [x0]
x_values = []
y_values = []
i = 0def f(x):f = x * exp(x) - 1return fwhile True:if diff(f(x),x).subs(x,x0) == 0:print('极值点：',x0)breakelse:x0 = x0 - f(x0)/diff(f(x),x).subs(x,x0)x_list.append(x0)if len(x_list) > 1:i += 1error = abs((x_list[-1] - x_list[-2]) / x_list[-1])x_values.append(i)y_values.append(error)if error == 0:print(f'迭代第{i}次后，误差为0')breakelse:passprint(f'所求方程式的根为{x_list[-1]}')#设置绘图风格
plt.style.use('ggplot')
#处理中文乱码
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
#坐标轴负号的处理
plt.rcParams['axes.unicode_minus']=False
#横坐标是迭代次数
#纵坐标是误差值
plt.plot(x_values,y_values,color = 'steelblue', # 折线颜色marker = 'o', # 折线图中添加圆点markersize = 3, # 点的大小)
# 修改x轴和y轴标签
plt.xlabel('迭代次数')
plt.ylabel('误差值')
# 显示图形
plt.show()

结果：

迭代第6次后，误差为0
所求方程式的根为0.567143290409784

带有区间的例题

求方程式：x3 - 0.165x2 + 3.99310**(-4) = 0在（0，0.11）的根

先看看不用迭代法计算的结果

from sympy import *
from sympy.abc import xdef func(x):return x**3 - 0.165*x**2 + 3.993*10**(-4)
result = solveset(func(x), x, Interval(0, 0.11))
print(result)

结果：

FiniteSet(0.0623775815137495)

约定一个误差，当误差小于某个数值的时候，迭代停止

代码：

from sympy import *x = symbols('x')
xl = 0  #区间下限
xu = 0.11  #区间上限
x0 = (xl+xu)/2  #迭代初始值
x_list = [x0]
i = 0def f(x):f = x**3 - 0.165*x**2 + 3.993*10**(-4)return fwhile True:if diff(f(x),x).subs(x,x0) == 0:print('极值点：',x0)breakelse:x0 = x0 - f(x0)/diff(f(x),x).subs(x,x0)x_list.append(x0)if len(x_list) > 1:i += 1error = abs((x_list[-1] - x_list[-2]) / x_list[-1])if error < 10**(-6):  print(f'迭代第{i}次后，误差小于10^-6')breakelse:passprint(f'所求方程式的根为{x_list[-1]}')

结果：

迭代第3次后，误差小于10^-6
所求方程式的根为0.0623775815137494

迭代至电脑默认误差为0

from sympy import *x = symbols('x')
xl = 0  #区间下限
xu = 0.11  #区间上限
x0 = (xl+xu)/2  #迭代初始值
x_list = [x0]
i = 0def f(x):f = x**3 - 0.165*x**2 + 3.993*10**(-4)return fwhile True:if diff(f(x),x).subs(x,x0) == 0:print('极值点：',x0)breakelse:x0 = x0 - f(x0)/diff(f(x),x).subs(x,x0)x_list.append(x0)if len(x_list) > 1:i += 1error = abs((x_list[-1] - x_list[-2]) / x_list[-1])if error == 0:print(f'迭代第{i}次后，误差等于0')breakelse:passprint(f'所求方程式的根为{x_list[-1]}')

结果：

迭代第5次后，误差等于0
所求方程式的根为0.0623775815137495

画迭代图

代码：

from sympy import *
import matplotlib.pyplot as pltx = symbols('x')
xl = 0  #区间下限
xu = 0.11  #区间上限
x0 = (xl+xu)/2  #迭代初始值
x_list = [x0]
i = 0def f(x):f = x**3 - 0.165*x**2 + 3.993*10**(-4)return fx_values = []
y_values = []
while True:if diff(f(x),x).subs(x,x0) == 0:print('极值点：',x0)breakelse:x0 = x0 - f(x0)/diff(f(x),x).subs(x,x0)x_list.append(x0)if len(x_list) > 1:i += 1error = abs((x_list[-1] - x_list[-2]) / x_list[-1])x_values.append(i)y_values.append(error)if error == 0:print(f'迭代第{i}次后，误差等于0')breakelse:passprint(f'所求方程式的根为{x_list[-1]}')#设置绘图风格
plt.style.use('ggplot')
#处理中文乱码
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
#坐标轴负号的处理
plt.rcParams['axes.unicode_minus']=False
#横坐标是迭代次数
#纵坐标是误差值
plt.plot(x_values,y_values,color = 'steelblue', # 折线颜色marker = 'o', # 折线图中添加圆点markersize = 3, # 点的大小)
# 修改x轴和y轴标签
plt.xlabel('迭代次数')
plt.ylabel('误差值')
# 显示图形
plt.show()

结果：

迭代第5次后，误差等于0
所求方程式的根为0.0623775815137495

牛顿法求解非线性方程组

牛顿法求解非线性方程组-附Python代码
解非线性方程组的牛顿迭代法(附Python代码)
python 实现（拟）牛顿法解非线性方程组
最优化方法：牛顿迭代法和拟牛顿迭代法

用牛顿迭代求解下面的非线性方程组

import numpy as npdef Fun(x,num):# 方程组在这里，三个变量分别是x的三个分量，num是未知数个数，这里是2，f是两个方程组i = numf = np.zeros((i),dtype=float)f[0] = x[0]**3-x[1]**2+1.    #x**3-y**2+1=0f[1] = x[0]**2-x[1]-1.    #x**2-y-1=0return f#计算雅可比矩阵的逆矩阵
def dfun(x,num):                         df = np.zeros((num,num),dtype=float)dx = 0.00001                           x1 = np.copy(x)    #x1 = xfor i in range(0,num):              # 求导数，i是列，j是行for j in range(0,num):x1 = np.copy(x)x1[j] = x1[j]+dx           #x+dxdf[i,j] = (Fun(x1,num)[i]-Fun(x,num)[i])/dx   #f(x+dx)-f（x）/dxdf_1 = np.linalg.inv(df)                              #计算逆矩阵return df_1def Newton(x,num):x1 = np.copy(x)  #x1 = x   1行num列i = 0delta = np.copy(x)while(np.sum(abs(delta)) > 1.e-8 and i < 100):  #控制循环次数x1 = x-np.dot(dfun(x,num),Fun(x,num))  #公式 x_k+1 = x_k - (dF(x_k))^(-1)·F(x_k)delta = x1-x     #比较x的变化x = x1i = i+1print(x)return x# 方程未知数的个数
num = 2                     
#初始值
x = np.array((-1,1), dtype=float)
print(x)
a = Newton(x,num)
print(a)#用sympy求解，检验牛顿迭代的正确性
import sympy
x,y = sympy.symbols('x,y')
print('方程的解：')
print(sympy.solve([x**3-y**2+1, x**2-y-1], [x,y]))

结果：

[-1.  1.]
[-1.14285918  0.28571694]
[-1.03069215  0.04974598]
[-1.00160721  0.00237137]
[-1.00000443e+00  6.30308922e-06]
[-1.00000000e+00  4.38330963e-11]
[-1.00000000e+00  2.44426795e-16]
[-1.00000000e+00  2.44426795e-16]
方程的解：
[(-1, 0), (0, -1), (2, 3)]

牛顿法求解非线性方程组——代码封装1

import numpy as np
import matplotlib.pyplot as plt#牛顿迭代
class Newton_Iteration():def __init__(self,):passdef Fun(self, x, num):# 方程组在这里，三个变量分别是x的三个分量，num是未知数个数，这里是2，f是两个方程组i = numf = np.zeros((i), dtype=float)X1, X2 = x[0], x[1]func = [X1 ** 2 + 4 * X2 ** 2 - 1, 4 * X1 ** 4 + X2 ** 2 - 1]f[0] = func[0]f[1] = func[1]return f# 计算雅可比矩阵的逆矩阵def dfun(self, x, num):df = np.zeros((num, num), dtype=float)dx = 0.00001x1 = np.copy(x)  # x1 = xfor i in range(0, num):  # 求导数，i是列，j是行for j in range(0, num):x1 = np.copy(x)x1[j] = x1[j] + dx  # x+dxdf[i, j] = (self.Fun(x1, num)[i] - self.Fun(x, num)[i]) / dx  # f(x+dx)-f（x）/dxdf_1 = np.linalg.inv(df)  # 计算逆矩阵return df_1#牛顿迭代def Newton(self, x, num):x1 = np.copy(x)  # x1 = x   1行num列i = 0x_values = []y_values = []delta = np.copy(x)while (np.sum(abs(delta)) > 1.e-8 and i < 100):  # 控制循环次数x1 = x - np.dot(self.dfun(x, num), self.Fun(x, num))  # 公式 x_k+1 = x_k - (dF(x_k))^(-1)·F(x_k)delta = x1 - x  # 比较x的变化x_values.append(i)y_values.append(delta)x = x1i = i + 1print(x)self.Drawing_error(x_values, y_values)return xdef Drawing_error(self,x_values,y_values):# 设置绘图风格plt.style.use('ggplot')# 处理中文乱码plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']# 坐标轴负号的处理plt.rcParams['axes.unicode_minus'] = False# 横坐标是迭代次数# 纵坐标是误差值plt.plot(x_values,y_values,color='steelblue',  # 折线颜色marker='o',  # 折线图中添加圆点markersize=3,  # 点的大小)# 修改x轴和y轴标签plt.xlabel('迭代次数')plt.ylabel('误差值')# 显示图形plt.show()if __name__ == '__main__':# 方程未知数的个数num = 2# 初始值x = np.array((-1, 1), dtype=float)# 方程组Newton_Iteration = Newton_Iteration()a = Newton_Iteration.Newton(x, num)print('方程组的解为：',a)

结果：

[-0.80644865  0.54838985]
[-0.70889633  0.38975774]
[-0.68372898  0.36586611]
[-0.68219953  0.36558393]
[-0.68219416  0.36558553]
[-0.68219416  0.36558553]
方程组的解为： [-0.68219416  0.36558553]

牛顿法求解非线性方程组——代码封装2

import numpy as np
import matplotlib.pyplot as plt
from sympy import *#牛顿迭代
class Newton_Iteration():def __init__(self, func, var_list):self.func = funcself.var_list = var_listpassdef Fun(self, x, num):# 方程组在这里，三个变量分别是x的三个分量，num是未知数个数，这里是2，f是两个方程组i = numf = np.zeros((i), dtype=float)f[0] = self.func[0].subs([(self.var_list[0],x[0]), (self.var_list[1],x[1])])f[1] = self.func[1].subs([(self.var_list[0],x[0]), (self.var_list[1],x[1])])return f# 计算雅可比矩阵的逆矩阵def dfun(self, x, num):df = np.zeros((num, num), dtype=float)dx = 0.00001x1 = np.copy(x)  # x1 = xfor i in range(0, num):  # 求导数，i是列，j是行for j in range(0, num):x1 = np.copy(x)x1[j] = x1[j] + dx  # x+dxdf[i, j] = (self.Fun(x1, num)[i] - self.Fun(x, num)[i]) / dx  # f(x+dx)-f（x）/dxdf_1 = np.linalg.inv(df)  # 计算逆矩阵return df_1#牛顿迭代def Newton(self, x, num):x1 = np.copy(x)  # x1 = x   1行num列i = 0x_values = []y_values = []delta = np.copy(x)while (np.sum(abs(delta)) > 1.e-8 and i < 100):  # 控制循环次数x1 = x - np.dot(self.dfun(x, num), self.Fun(x, num))  # 公式 x_k+1 = x_k - (dF(x_k))^(-1)·F(x_k)delta = x1 - x  # 比较x的变化x_values.append(i)y_values.append(delta)x = x1i = i + 1print(x)self.Drawing_error(x_values, y_values)return xdef Drawing_error(self,x_values,y_values):# 设置绘图风格plt.style.use('ggplot')# 处理中文乱码plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']# 坐标轴负号的处理plt.rcParams['axes.unicode_minus'] = False# 横坐标是迭代次数# 纵坐标是误差值plt.plot(x_values,y_values,color='steelblue',  # 折线颜色marker='o',  # 折线图中添加圆点markersize=3,  # 点的大小)# 修改x轴和y轴标签plt.xlabel('迭代次数')plt.ylabel('误差值')# 显示图形plt.show()if __name__ == '__main__':# 方程未知数的个数num = 2# 初始值x = np.array((-1, 1), dtype=float)X1, X2 = symbols('X1, X2')var_list = [X1, X2]# 方程组func = [X1 ** 2 + 4 * X2 ** 2 - 1, 4 * X1 ** 4 + X2 ** 2 - 1]Newton_Iteration = Newton_Iteration(func, var_list)a = Newton_Iteration.Newton(x, num)print('方程组的解为：',a)

结果：

[-0.80644865  0.54838985]
[-0.70889633  0.38975774]
[-0.68372898  0.36586611]
[-0.68219953  0.36558393]
[-0.68219416  0.36558553]
[-0.68219416  0.36558553]
方程组的解为： [-0.68219416  0.36558553]