转自 LeetCode 解答

一篇解释得很细的文章

---

  牛顿迭代法是一种可以用来快速求解函数零点的方法。

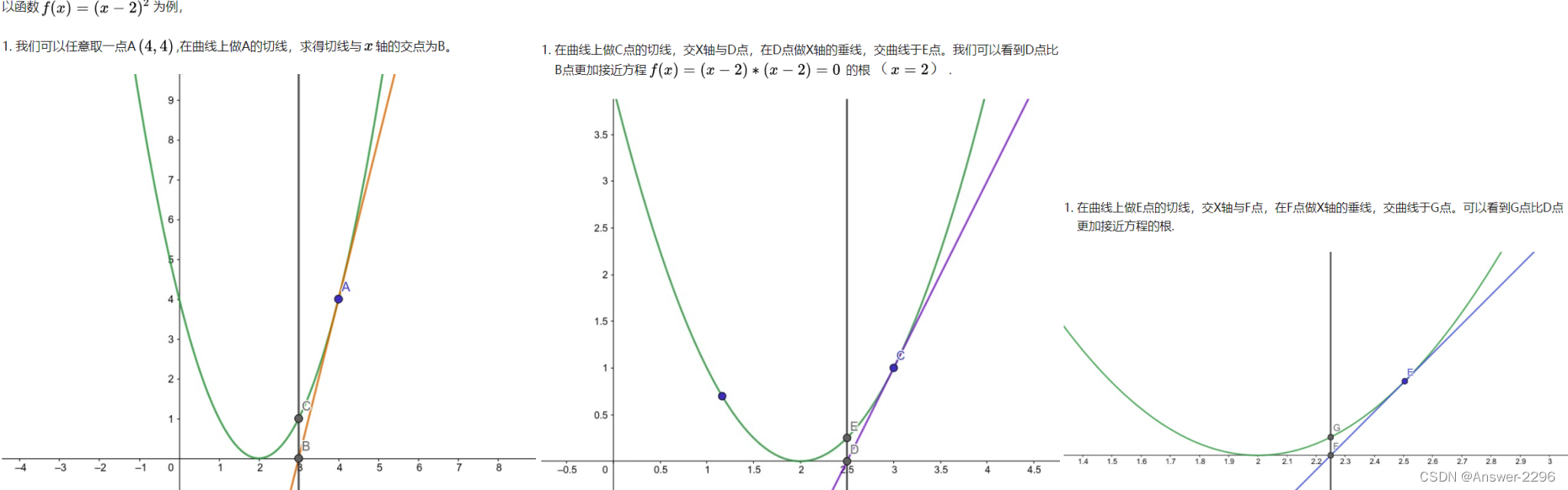
  以 LeetCode 上的一题为例：模拟 int sqrt(x) 函数，返回的开方值向下取整。

  为了叙述方便，我们用 C 表示待求出平方根的那个整数。显然，C 的平方根就是函数
$$y=f(x)=x^2-C$$
  的零点。

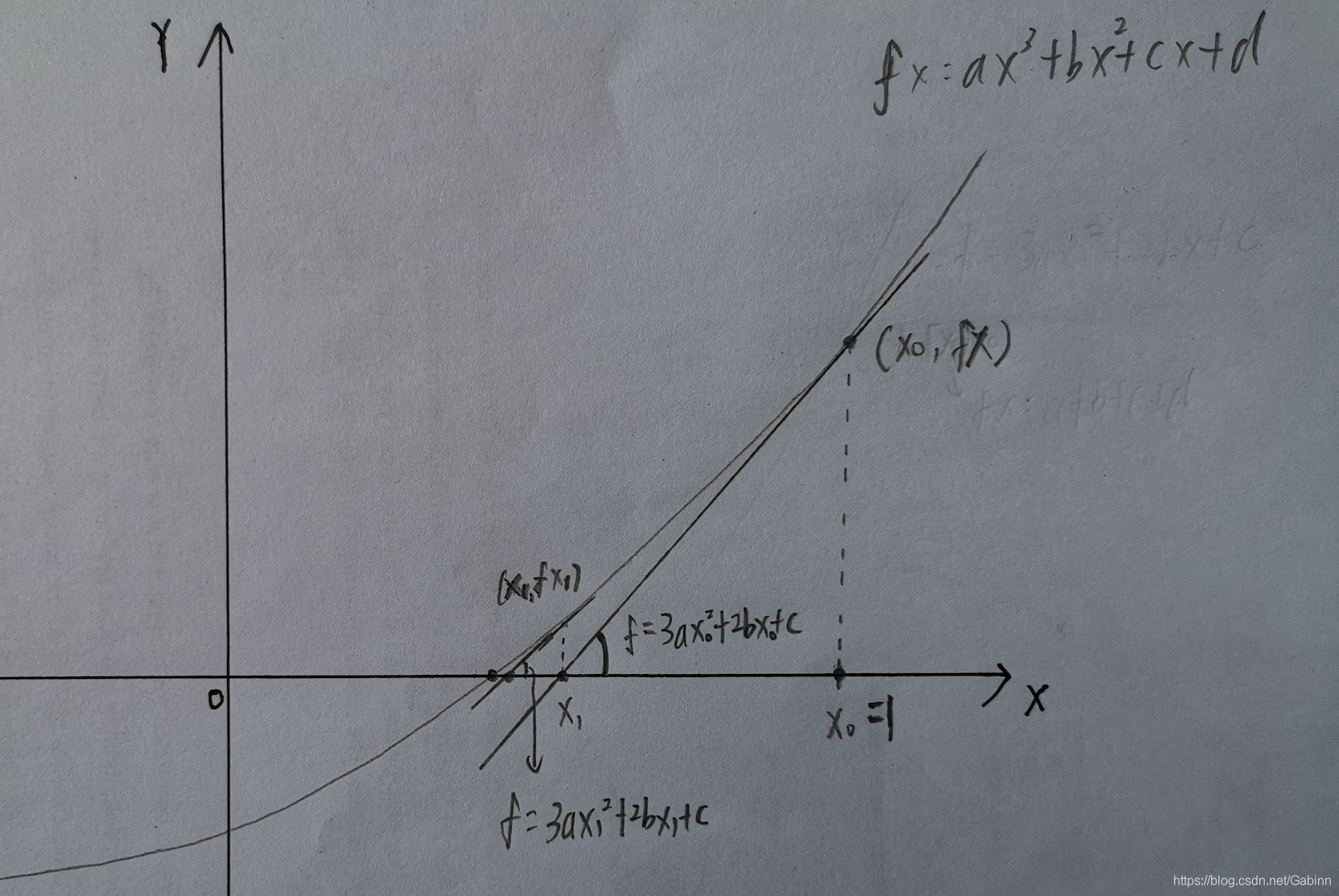
  牛顿迭代法的本质是借助泰勒级数，从初始值开始快速向零点逼近。我们任取一个 $x_0$ 作为初始值，在每一步的迭代中，我们找到图像上的点 $(x_i,f(x_i))$ ，过该点做一条斜率为该点导数 $f^{\prime }(x_i)$ 的直线，直线与 x 轴的交点记为 $x_{i+1}$，$x_{i+1}$ 相对于 $x_i$ 而言距离零点更加接近。进过多次迭代后，就能得到一个非常接近零点的与 x 轴的交点。

  下图给出了从 $x_0$ 开始迭代两次，得到 $x_1$ 和 $x_2$ 的过程：

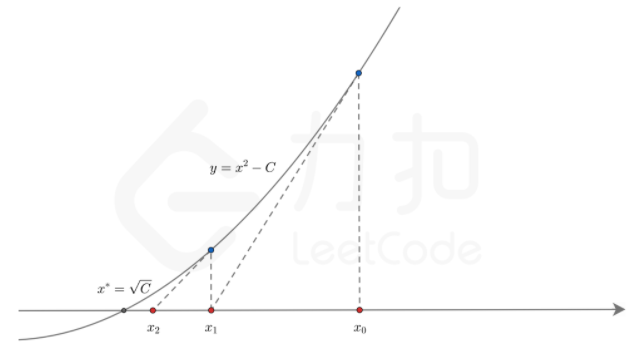
  首先，我们选择 $x_0=C$ 作为初始值。

  在每一步的迭代中，通过当前与 x 轴的交点 $x_i$ ，得到函数图像上的一点 $(x_i,x^2-C)$ ，做一条斜率为 $f^{\prime }(x_i)=2x_i$ 的直线，直线方程为：
$$y-y_0=k(x-x_0)$$

$$y=2x_i(x-x_i)+x_i^2-C$$

  因此，与 x 轴的交点为方程 $2x_{i}x-(x_i^2+C)=0$ 的解，即为新的迭代结果 $x_{i+1}$ ：
$$x_{i+1}=\frac{1}{2}(x_i+\frac{C}{x_i})$$
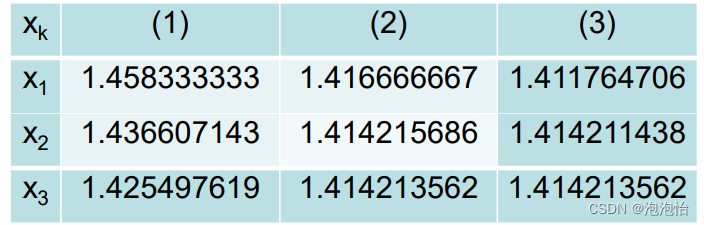
  在进行 k 次迭代之后，$x_k$ 与真实值 $\sqrt{C}$ 足够接近，即可作为答案。

  选择 $x_0=C$ 作为初始值的原因：

  因为函数 $y=x^2-C$ 有两个零点 $-\sqrt{C}$ 和 $\sqrt{C}$。而我们想找的是 $\sqrt{C}$，如果初始值比较小的话，有可能迭代到 $-\sqrt{C}$ 这个零点，因此选择 $x_0=C$ 作为初始值。且每次迭代均有 $x_{i+1}<x_i$，零点 $\sqrt{C}$ 在其左侧，因此我们一定会迭代到这个零点。

  迭代终止条件：

  每一次迭代，我们都会离零点更近一步，所以当两次迭代的距离非常近时，就可以认为是已经非常逼近零点了，也就能将其作为答案。判断接近程度可以使用一个非常小的值来做比较，如 $x_{i+1}-x_i<10^{-6}$ 。

  C 代码如下：

int mySqrt(int x){if (x == 0) {return 0;}double x0 = x, c = x;while (true) {double xi = 0.5 * (x0 + c / x0);if (fabs(x0 - xi) < 1e-6) {break;}x0 = xi;}return (int)x0;
}