简介

牛顿迭代法（简称牛顿法）由英国著名的数学家牛顿爵士最早提出。但是，这一方法在牛顿生前并未公开发表。

牛顿法的作用是使用迭代的方法来求解函数方程的根。简单地说，牛顿法就是不断求取切线的过程。

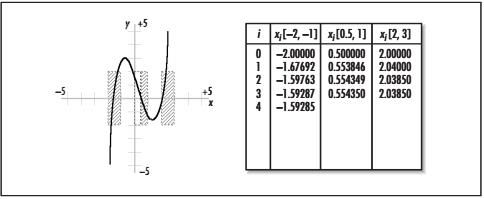
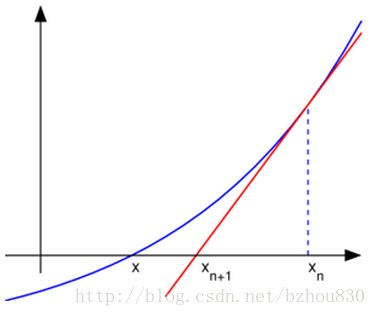
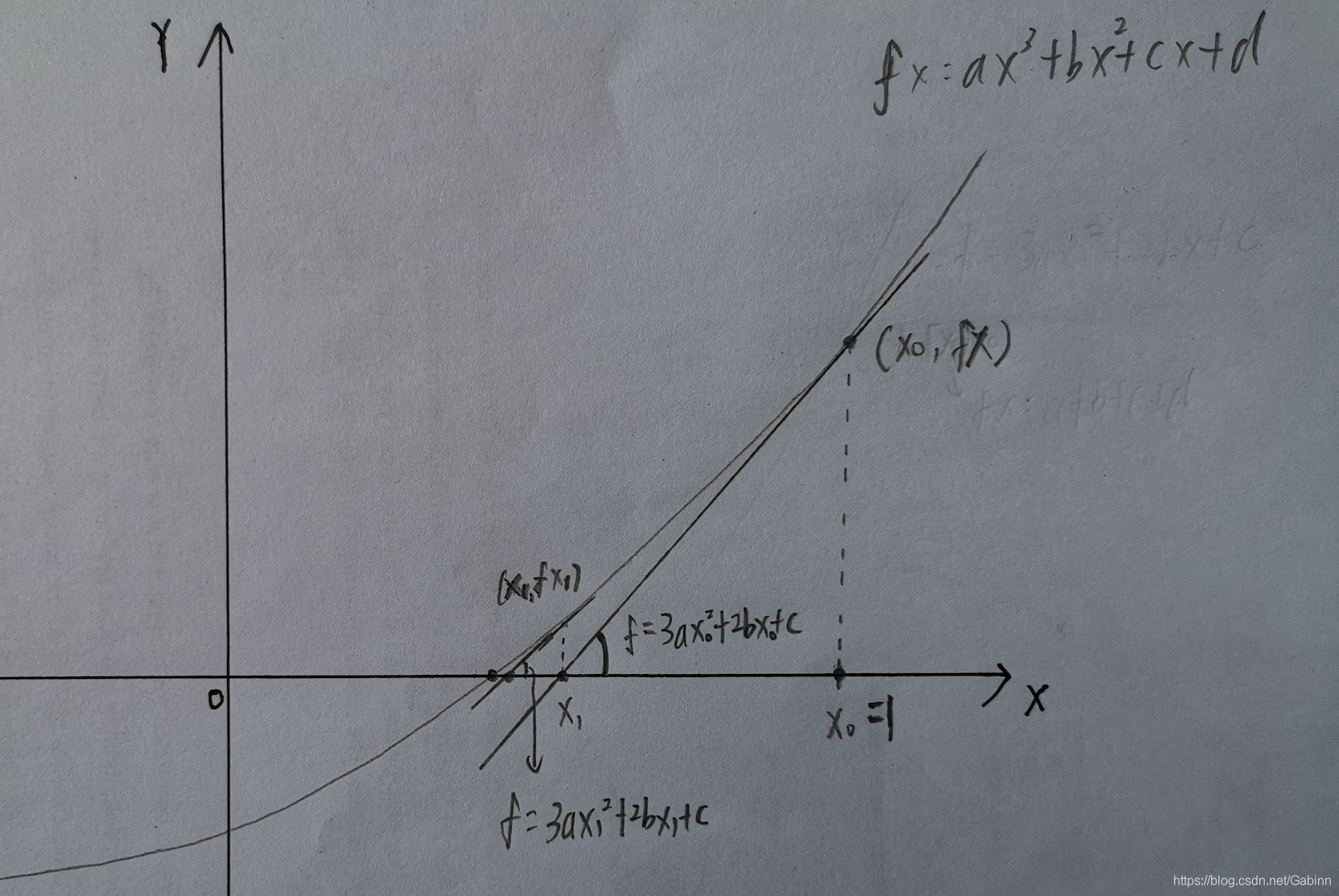
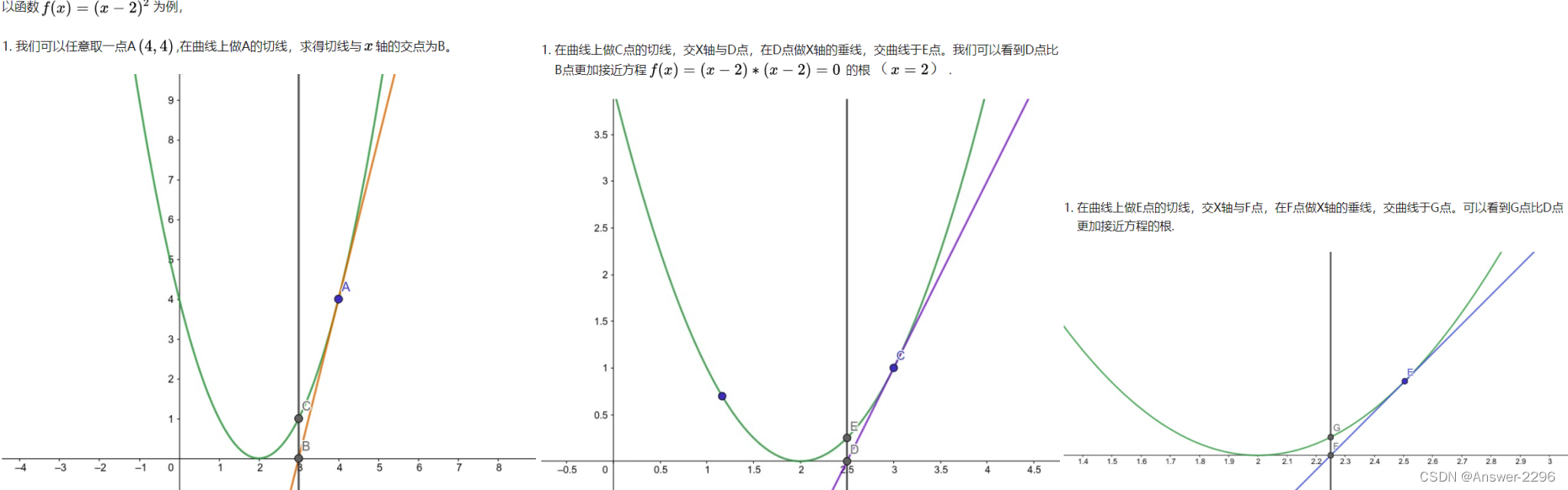
对于形如f(x)=0的方程，首先任意估算一个解x0，再把该估计值代入原方程中。由于一般不会正好选择到正确的解，所以有f(x)=a。这时计算函数在x0处的斜率，和这条斜率与x轴的交点x1。

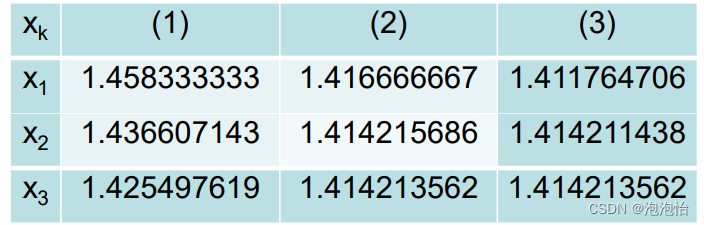
f(x)=0中精确解的意义是，当取得解的时候，函数值为零（即f(x)的精确解是函数的零点）。因此，x1比x0更加接近精确的解。只要不断以此方法更新x，就可以取得无限接近的精确的解。

但是，有可能会遇到牛顿迭代法无法收敛的情况。比如函数有多个零点，或者函数不连续的时候。

牛顿法举例

下面介绍使用牛顿迭代法求方根的例子。牛顿迭代法是已知的实现求方根最快的方法之一,只需要迭代几次后就能得到相当精确的结果。

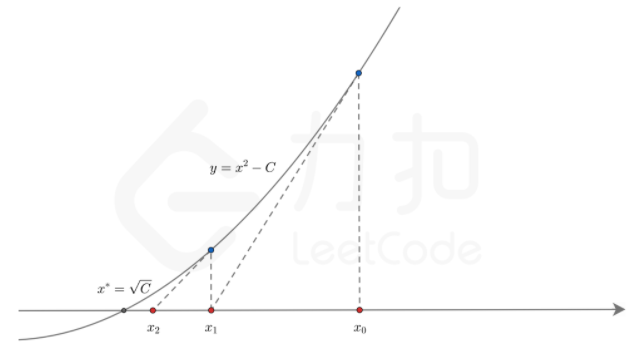
首先设x的m次方根为a。

下面程序使用牛顿法求解平方根。

const float EPS = 0.00001; 
int sqrt(double x) { if(x == 0) return 0; double result = x; /*Use double to avoid possible overflow*/ double lastValue; do{ lastValue = result; result = result / 2.0f + x / 2.0f / result; }while(abs(result - lastValue) > EPS);return (double)result;}

更快的方法

文献2提到了比上述程序更快的求解平方根的非典型牛顿迭代法。介绍如下。

1999年12月，美国id Software公司发布了名为“雷神之锤III”的电子游戏。它是第一个支持软件加速的游戏，取得了极大成功。（由于影响力过大，文化部于2004年将它列入了非法游戏名单）

雷神之锤III并不是id Software公司的第一次成功。早在1993年开始，这家公司就以“毁灭战士”系列游戏名闻天下。1995年，“毁灭战士”的安装数超过了当年微软的windows 95。据传比尔盖茨才曾经考虑买下id software。（id software公司后来被推出过“上古卷轴”系列的Bethesda公司买下）

id Software所取得的成功很大程度上要归功于它的创始人约翰·卡马克。马克尔也是一个著名的程序员，他是id Software游戏引擎的主要负责人。 回到刚才提到的雷神之锤，马克尔是开源软件的积极推动者，他于2005年公布了雷神之锤III的源代码。至此人们得以通过研究这款游戏引擎的源文件来查看它成功的秘密。

在其中一个名字为q_math.c的文件中发现了如下代码段。

float Q_rsqrt( float number ) { long i; float x2, y; const float threehalfs = 1.5F;x2 = number * 0.5F; y = number; i = * ( long * ) &y; // evil floating point bit level hacking i = 0x5f3759df - ( i >> 1 ); // what the fuck? y = * ( float * ) &i; y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration // y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed#ifndef Q3_VM #ifdef __linux__ assert( !isnan(y) ); // bk010122 - FPE?#endif#endif return y; 
}

这段代码的作用就是求number的平方根，并且返回它的倒数。

经过测试，它的效率比上述牛顿法程序要快几十倍。也比c++标准库的sqrt()函数要快好几倍。此段代码有一个奇怪的句子：

i = 0x5f3759df - ( i >> 1 ); // what the fuck? 

这句话的注释是“what the fuck?”，翻译过来就是“我靠？”

任何受过程序训练的人看到这句大概都会在想，这句话到底在搞什么鸟？

之所以会出现这种奇怪的注释，要么是此段程序的作者（可能是马克尔）根本不知道该如何解释清楚，或者是维护这段程序的程序员完全看不懂这句话，所以有点儿抓毛。而实际上，它的作用（再加上y = y * ( threehalfs - ( x2 * y * y ) )这句牛顿迭代）就是求平方根。

至于是为什么，本博主也不知道。

以雷神之锤III程序为蓝本可以写出比sqrt()更强大的求平方根函数：

int sqrt(float x) { if(x == 0) return 0; float result = x; float xhalf = 0.5f*result; int i = *(int*)&result; i = 0x5f375a86- (i>>1); // what the fuck? result = *(float*)&i; result = result*(1.5f-xhalf*result*result); // Newton step, repeating increases accuracy result = result*(1.5f-xhalf*result*result); return 1.0f/result; 
}

参考文献:
1.wikipedia.org
2.http://www.2cto.com/kf/201206/137256.html