目录

•写在前面

•前戏-二分法实现

•牛顿迭代法

代码实现

---

•写在前面

求开方这件事儿，很多时候用一个sqrt方法就搞定了，很少有趣思考这底层的实现到底是用什么方法完成的。正好我遇到了需要实现sqrt方法，这里就仔细的讲解一下如何去实现sqrt，当然啦，这里会进行一些数学原理的推算，不想看这些数学原理的推算的，也可以直接跳过，看文字描述的原理思路，我分好目录了，哈哈哈。

•前戏-二分法实现

求开方这个问题，其实就是对  进行求解，很多时候我们比较直观的一种思路就是找到一个数，使得这个数的平方等于目标数值就可以了，使用二分法搜索平方根的思想很简单，就类似于小时候我们看的电视节目中的“猜价格”游戏，高了就往低了猜，低了就往高了猜，范围越来越小。因此，使用二分法猜算术平方根就很自然。一个数的平方根肯定不会超过它自己，不过直觉还告诉我们，一个数的平方根最多不会超过它的一半，例如 8 的平方根，8 的一半是 4， 。这个思路就简单多了，我们只要在0到这个数的一半，进行二分查找合适的数就可以了。这种思路比较简单，我这里直接贴实现代码。

//这里我就直接使用整数，求解最接近的整数就可以了，精
//确到小数，毕竟我们想要学习的是思想
public int mySqrt(int x){long left = 0;long right = Integer.MAX_VALUE;while (left < right){long mid = (left + right + 1) >>> 1;  //求解中位数的一种方式，无符号右位移long square = mid * mid;if(square > x){right = mid - 1;}else {left = mid;}}return (int)left;
}

•牛顿迭代法

我们求解数的开方，有很多方法，这里我们先从数学上进行讲解，这样可以从本质的理解牛顿迭代法。首先我们求解数的开方，其实就是求解某个多次方程的根式解。

我们需要先来理解一个知识点，就是“切线是曲线的线性逼近”，这是什么意思呢？我们用  进行举例，图如下：

最左边是  的图，我们随便选一点  上的一点  作它的切线，把点命名为A，然后不断放大A点以及切线，我们就可以看到，切线非常接近曲线。因为切线是一条直线（也就是线性的），所以我们可以说，A点的切线是  的线性逼近。离A点距离越近，这种逼近的效果也就越好，也就是说，切线与曲线之间的误差越小。所以我们可以说在A点附近，切线  。

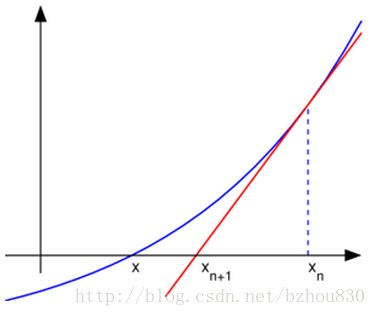
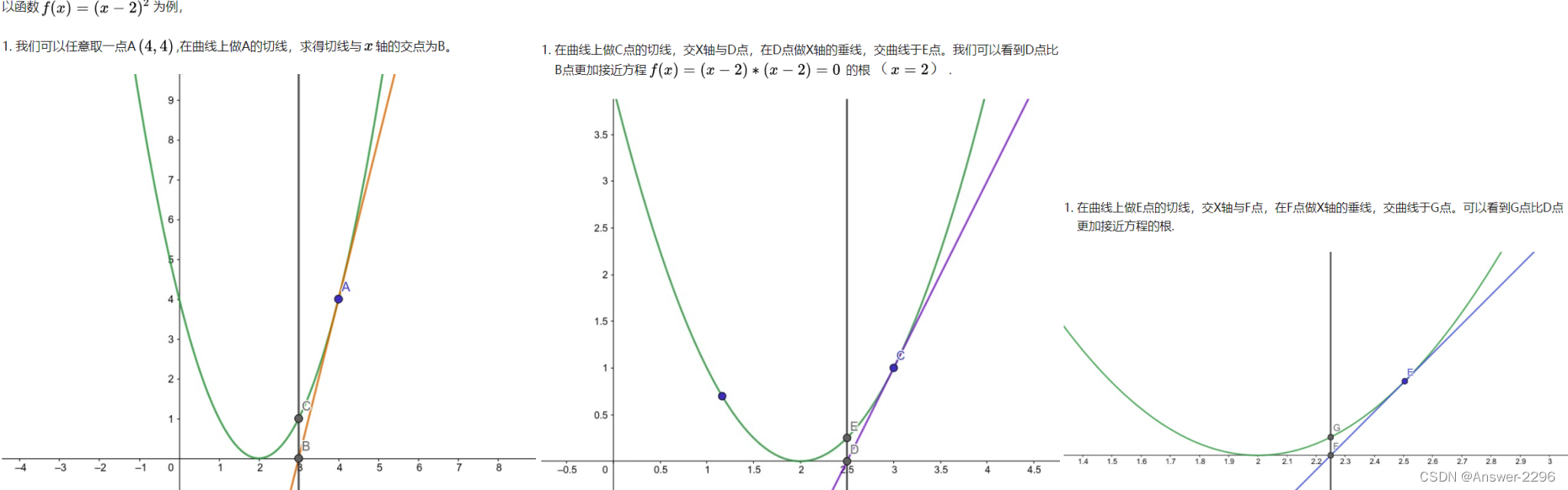
有了这个知识点之后，我们就会发现，切线既然可以近似曲线，那么我们岂不是直接研究这个切线就可以了嘛，现在我们来看下图，从左到右，从上到下四张图

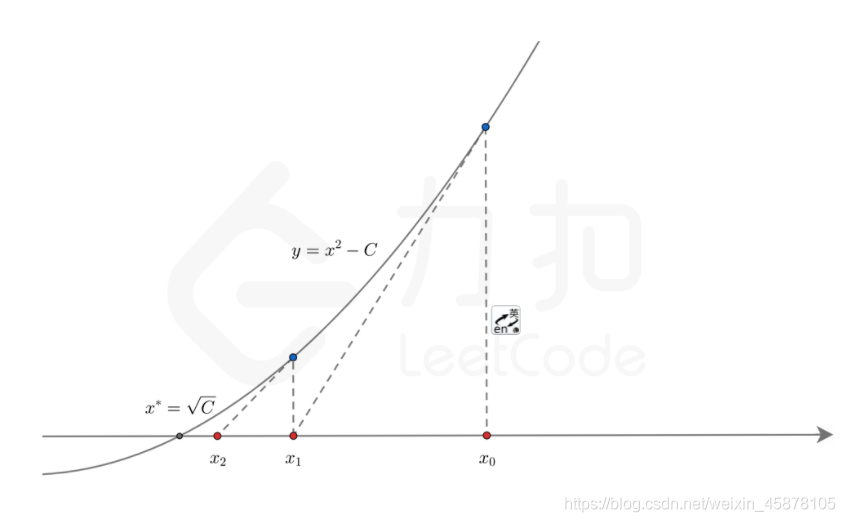
上图我们可以知道，最开始的第一张图中，我们随便找一个点，然后过该点做切线，我们会发现，这条切线的根（也就是和x轴相交的点）与曲线的根（曲线和x轴相交的点）有一定的距离。怎么办呢？没关系，这个时候我们看第二张图，我们先过切线的根的那个点做x轴的垂线，这条垂线会和曲线相交于一个B点，然后我们再在这个B点做切线，我们会发现这条切线的根离曲线的根更近了，如此重复这个步骤，在这个过程中，我们会发现，切线的根会越来越接近曲线的根。经过多次迭代之后，我们会发现我们非常接近曲线的根了，用专业的术语来讲，就是迭代收敛了。

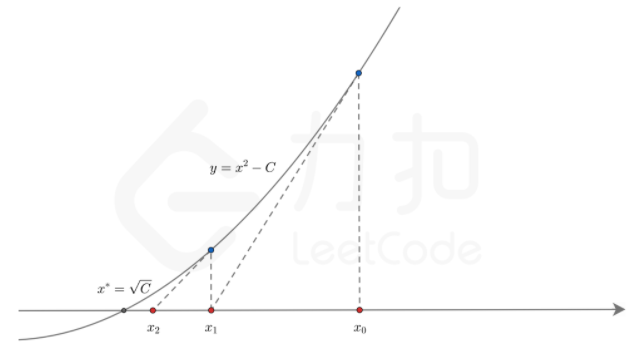
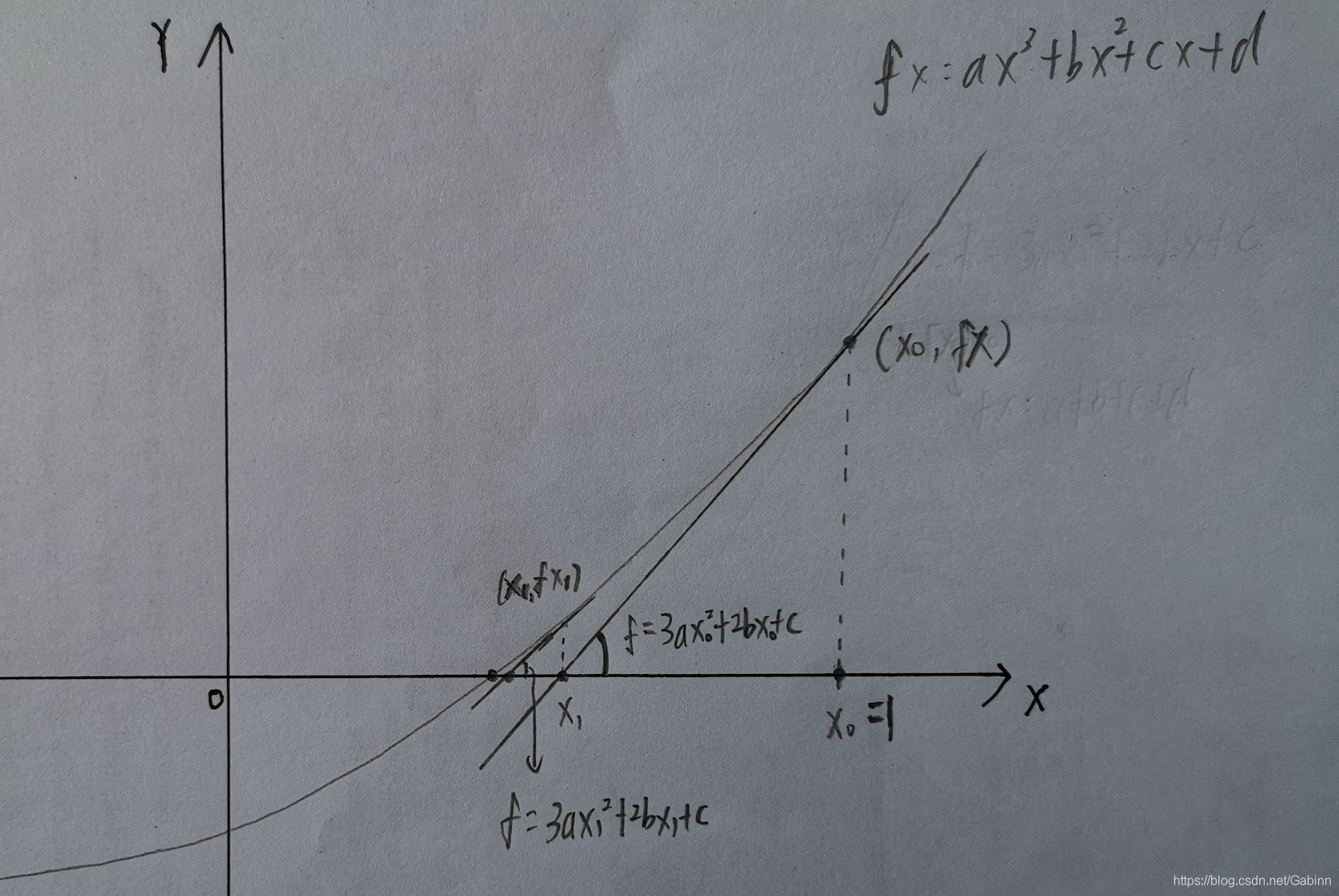
现在我们来推到，首先假设已知曲线方程  ，我们现在在  点做切线，求  ，图如下：

容易得出， 点的切线方程为  ，要求  ，即相当于求  的解也就是 得到 ，这个时候我们就需要思考一个问题，我们每次选中的条，使用这个方法进行求解，一定会收敛么，我们先来看看收敛的充分条件：

若  二阶可导，那么在待求的零点  周围存在一个区域，只要起始点  位于这个邻近区域内，那么我们使用这个方法必定收敛，换句话说，如果我们选中的点不在这个邻近区域内，就不会收敛，举个例子，比如我们不小心的选中了驻点，那么就不会收敛，如下图

这种情况是我们选中的点不在邻近区域内，导致不收敛，有一些情况是如论我们怎么选择，都不会收敛，比如在  的曲线，不论怎么选择起始点，越迭代就越远离根点，如下图

还有一种就是不断的循环震荡不收敛，比如  曲线，如下图

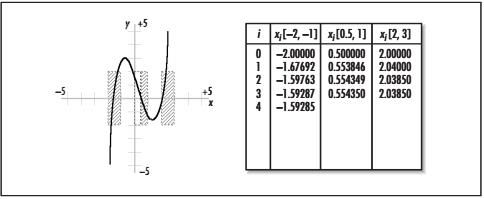
还有一种就是不能完整的求出所有的根，比如  这种多根的函数，因为我们只能求到附近的根，当然，也可能因为我们选择的起始点不同的原因，导致我们求到了较远的根，如下图

所以经过上面的讨论，我们使用牛顿迭代法的时候，需要注意一下几个问题

• 函数在整个定义域内最好是二阶可导的
• 起始点对求根计算影响重大，可以增加一些别的判断手段进行试错

代码实现

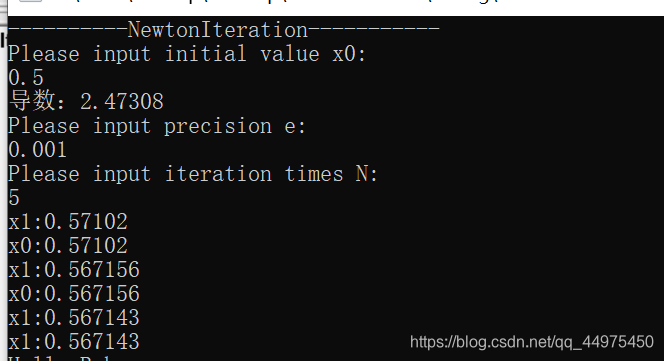
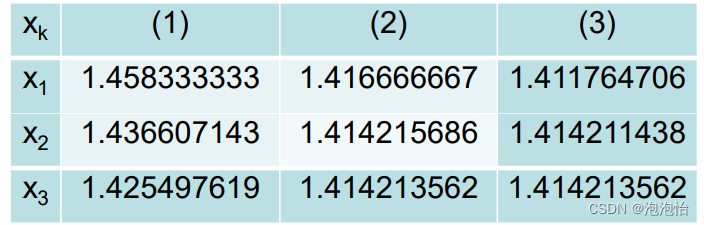
为了得到代码，我们通过一个简单的运算，来简略的说明牛顿迭代法（但并不是说上面的数学讨论是废话，毕竟数学的美，要自己体会，哈哈哈），如下图

public int mySqrt(int x){long a = x;while (a * a > x){a = (a + x / a) / 2;}return (int) a;
}