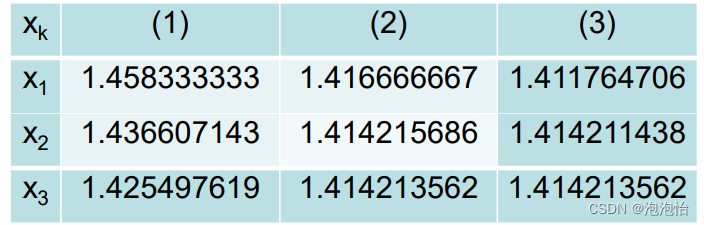
五次及以上多项式方程没有根式解(就是没有像二次方程那样的万能公式),这个是被伽罗瓦用群论做出的最著名的结论。
但是,没有王屠夫难道非得吃带毛猪?工作生活中还是有诸多求解高次方程的真实需求(比如行星的轨道计算,往往就是涉及到很复杂的高次方程),这日子可怎么过下去啊?
没有根式解不意味着方程解不出来,数学家也提供了很多方法,牛顿迭代法就是其中一种。
1 切线是曲线的线性逼近
要讲牛顿迭代法之前我们先说一个关键问题:切线是曲线的线性逼近。
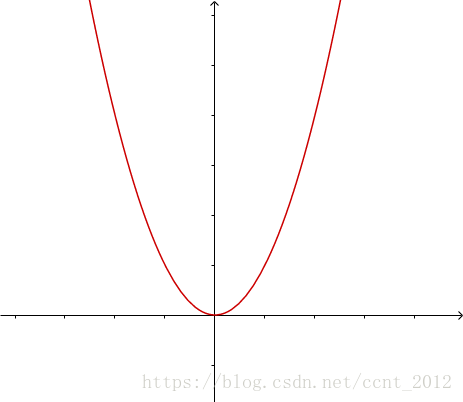
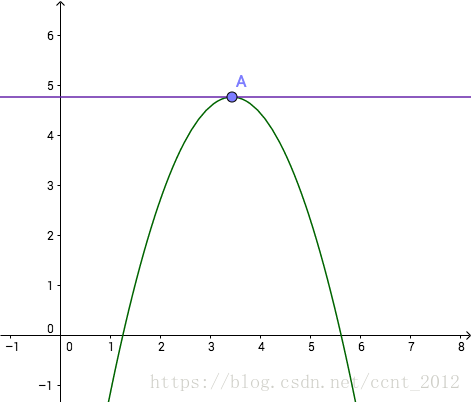
这个是什么意思呢?我们来看一看,下面是 的图像:
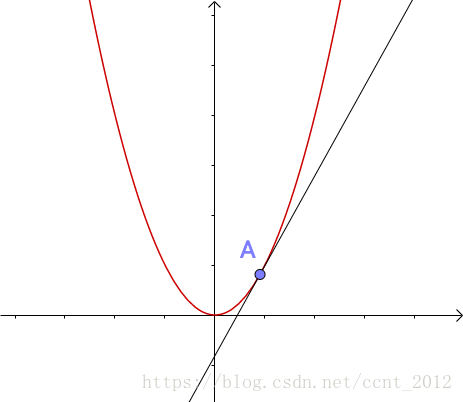
我们随便选一点 上的一点
做它的切线:
我们在A点处放大图像:
上图中,红色的线是 ,黑色的是A点处的切线,可以看出放大之后切线和
非常接近了。很明显,如果我们进一步放大图像,A点切线就越接近
。
可以自己动手试试:
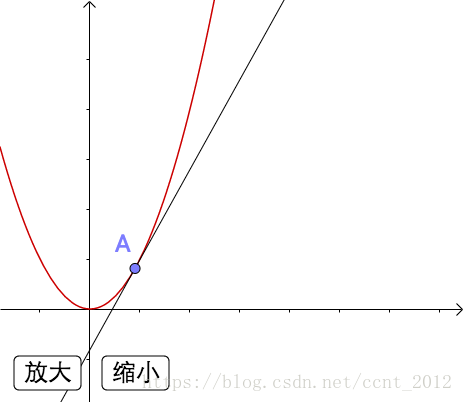
此处有互动内容,点击此处前往操作。
因为切线是一条直线(也就是线性的),所以我们可以说,A点的切线是 的线性逼近。离A点距离越近,这种逼近的效果也就越好,也就是说,切线与曲线之间的误差越小。所以我们可以说在A点附近,“切线
”。
2 牛顿-拉弗森方法的几何直觉
牛顿迭代法又称为牛顿-拉弗森方法,实际上是由牛顿、拉弗森(又是一个被牛顿大名掩盖的家伙)各自独立提出来的。
牛顿-拉弗森方法提出来的思路就是利用切线是曲线的线性逼近这个思想。
牛顿、拉弗森们想啊,切线多简单啊,研究起来多容易啊,既然切线可以近似于曲线,我直接研究切线的根不就成了。
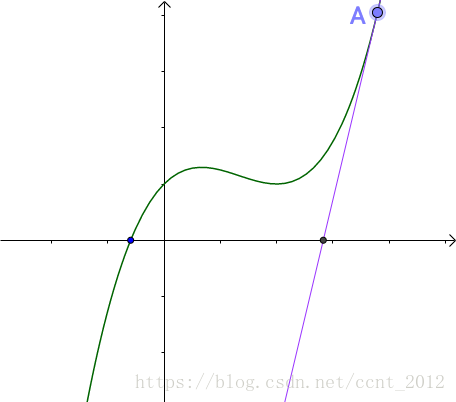
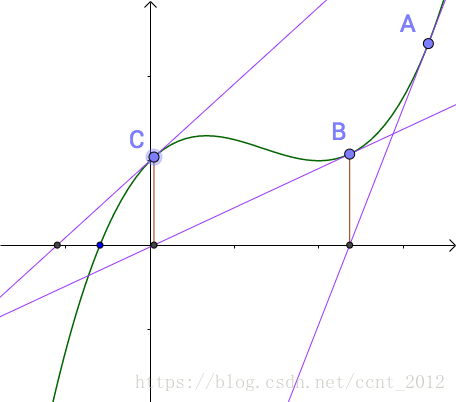
然后他们观察到这么一个事实:
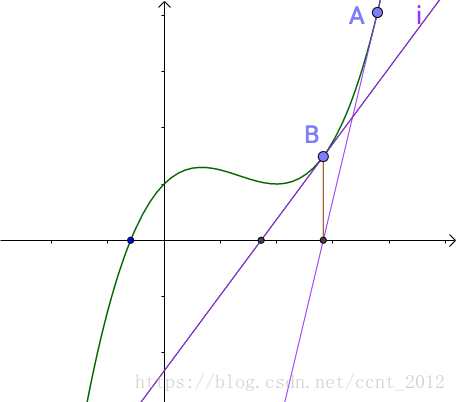
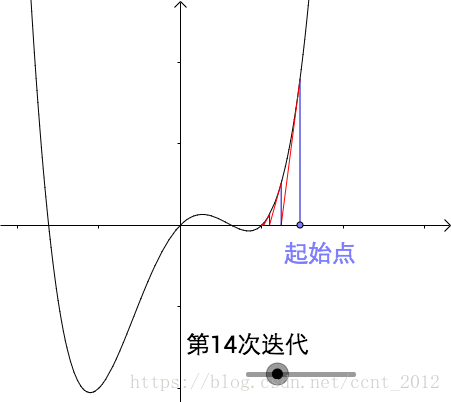
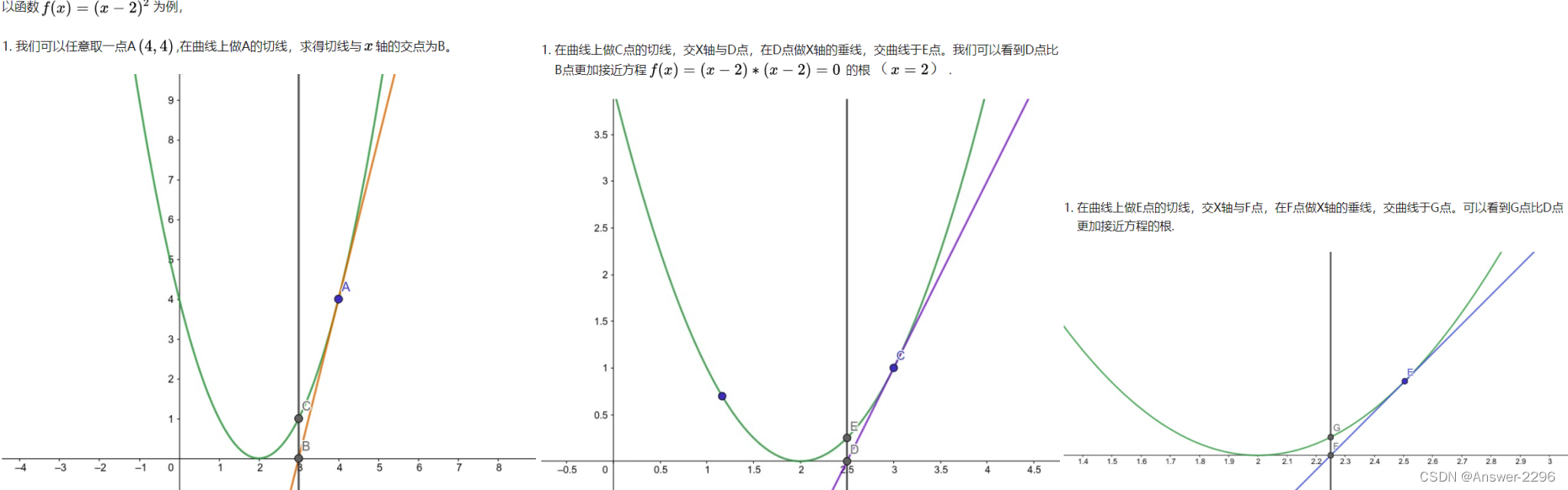
随便找一个曲线上的A点(为什么随便找,根据切线是切点附近的曲线的近似,应该在根点附近找,但是很显然我们现在还不知道根点在哪里),做一个切线,切线的根(就是和x轴的交点)与曲线的根,还有一定的距离。牛顿、拉弗森们想,没关系,我们从这个切线的根出发,做一根垂线,和曲线相交于B点,继续重复刚才的工作:
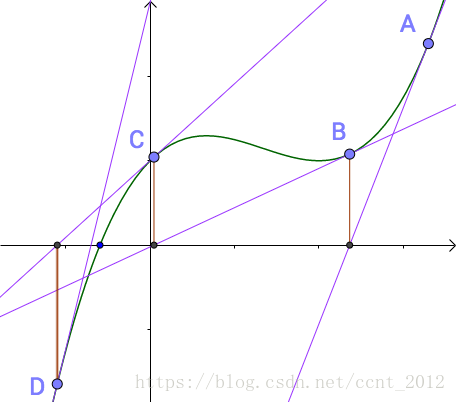
之前说过,B点比之前A点更接近曲线的根点,牛顿、拉弗森们很兴奋,继续重复刚才的工作:
第四次就已经很接近曲线的根了:
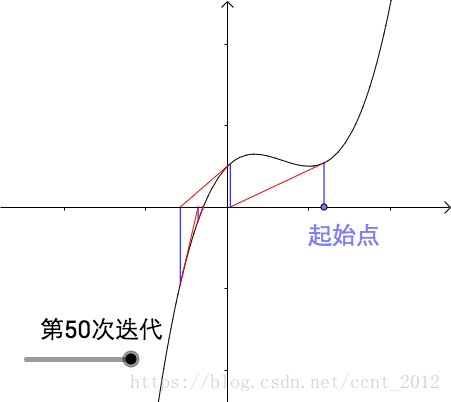
经过多次迭代后会越来越接近曲线的根(下图进行了50次迭代,哪怕经过无数次迭代也只会更接近曲线的根,用数学术语来说就是,迭代收敛了):
3 牛顿-拉弗森方法的代数解法
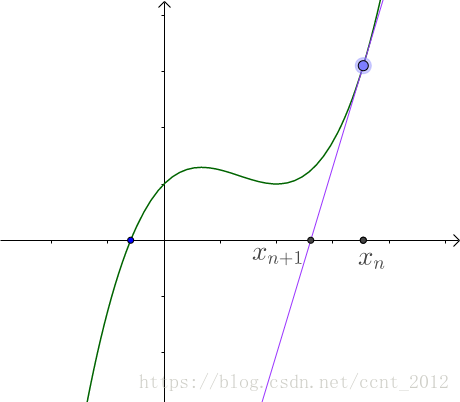
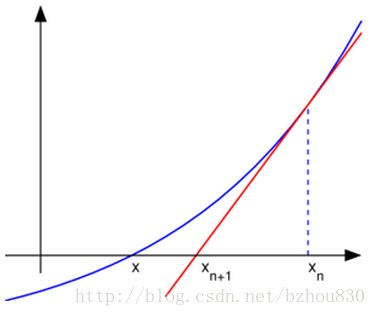
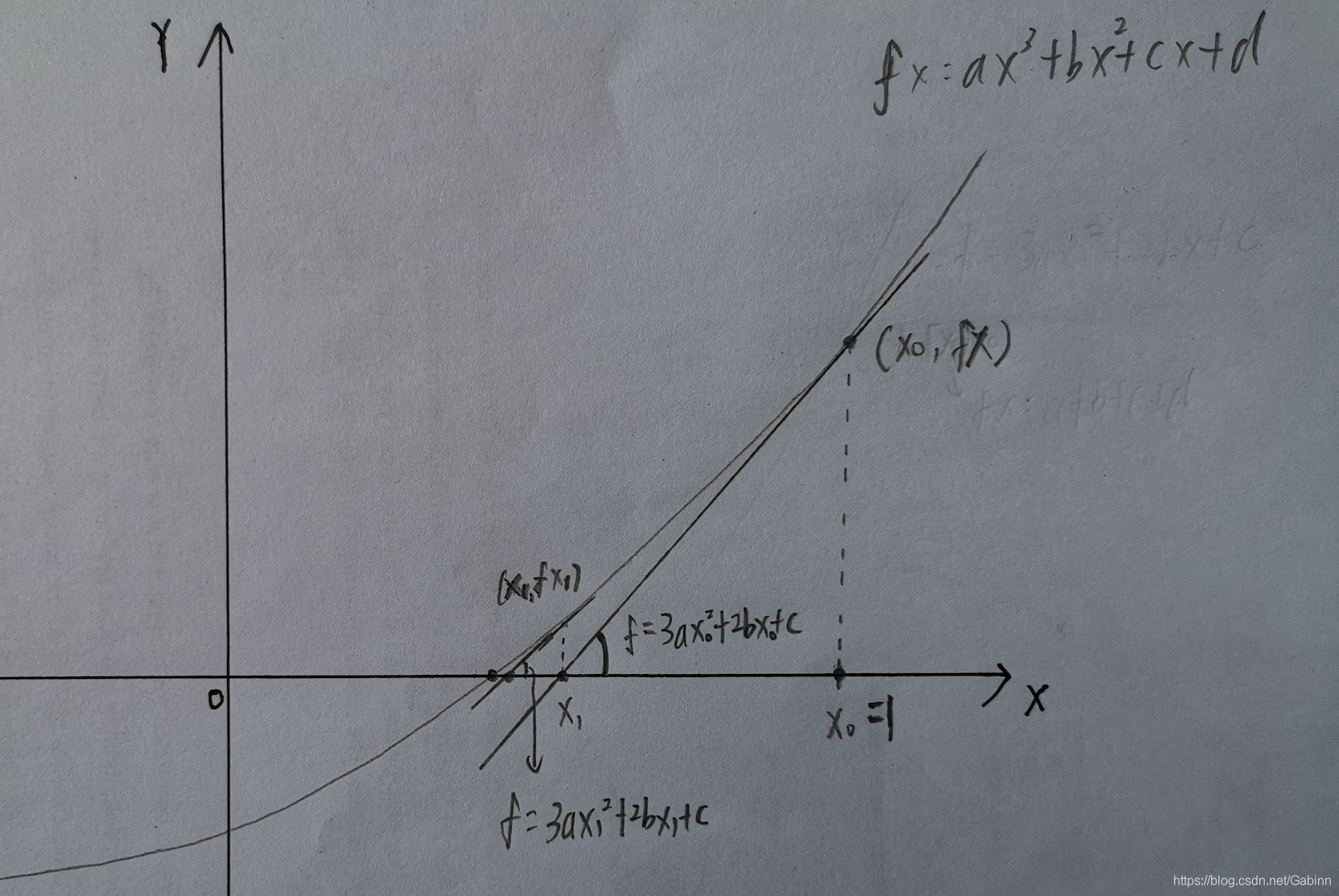
已知曲线方程 ,我们在
点做切线,求
:
容易得出, 点的切线方程为:
。
要求 ,即相当于求
的解,即
:
4 牛顿-拉弗森方法是否总是收敛(总是可以求得足够近似的根)?
牛顿-拉弗森方法源于直觉,这种直觉本身有一定程度的合理性。
我们来看看收敛的充分条件:
若二阶可导,那么在待求的零点
周围存在一个区域,只要起始点
位于这个邻近区域内,那么牛顿-拉弗森方法必定收敛。
也就是说,在这个区域内,用切线代替曲线这个直觉是合理的。但是,因为我们不知道根点到底在哪里,所以起始点 选择就不一定在这个区域内,那么这个直觉就不可靠了。
4.1 驻点
起始点不幸选择了驻点,从几何上看切线根本没有根。
从代数上看, 没有意义。
4.2 越来越远离的不收敛
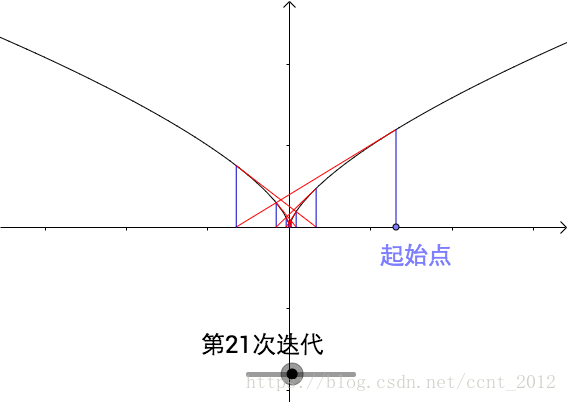
下面是 的曲线,不论怎么选择起始点,越迭代就越远离根点:
从代数上看, ,就是说下一个点比上一个点更远离根点。
此处根点很显然是0点,而 是不存在的。
4.3 循环震荡的不收敛
还有一种更酸爽的不收敛,就是不断的循环震荡。
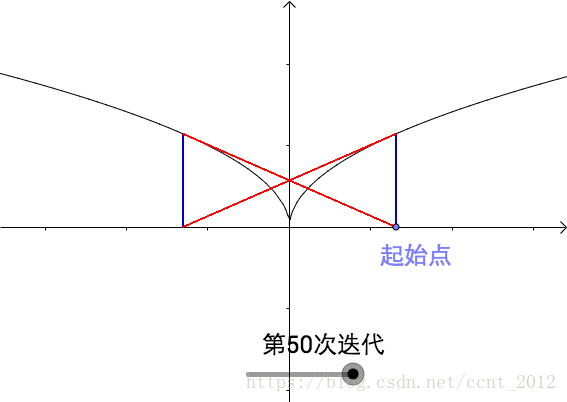
比如下面是 的曲线:
很漂亮的图像吧。从代数上看就是 造成的。
由于选择的起始点不对,造成这种循环的情况其实还挺多,在很多曲线的某些点都会出现这种情况。
此处根点也是0点,而 是不存在的。但是不一定
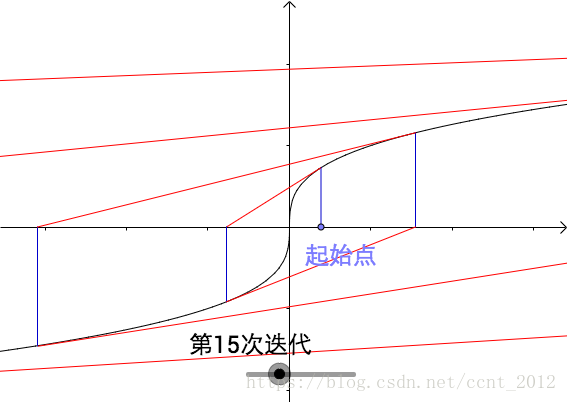
不存在就无法用牛顿-拉弗森方法求解,比如
依然可以用牛顿-拉弗森方法:
这是因为之前说的收敛判断条件只是充分条件。
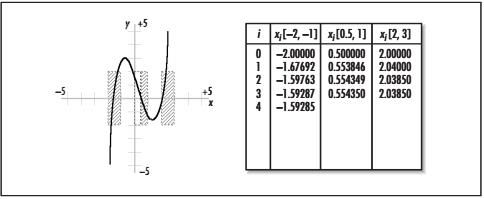
4.4 不能完整求出所有的根
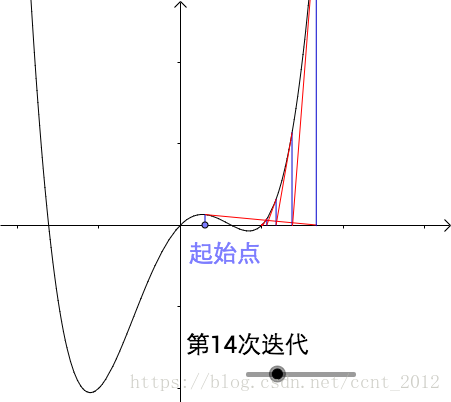
比如 这种有多个根的函数,因为选择的起始点,只能求到附近的根:
也可能想求附近的根,由于选择的起始点不对,结果求到远处的根:
4.5 自己动手试试
通过按钮可以切换函数,拖动“起始点”也会有惊喜:
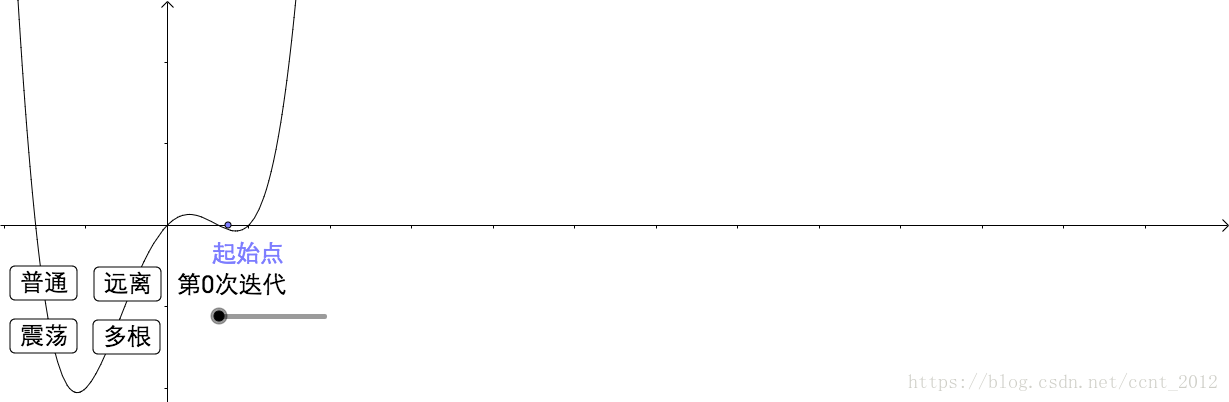
此处有互动内容,点击此处前往操作。
4.6 总结
应用牛顿-拉弗森方法,要注意以下问题:
-
函数在整个定义域内最好是二阶可导的
-
起始点对求根计算影响重大,可以增加一些别的判断手段进行试错
5 牛顿-拉弗森方法的应用
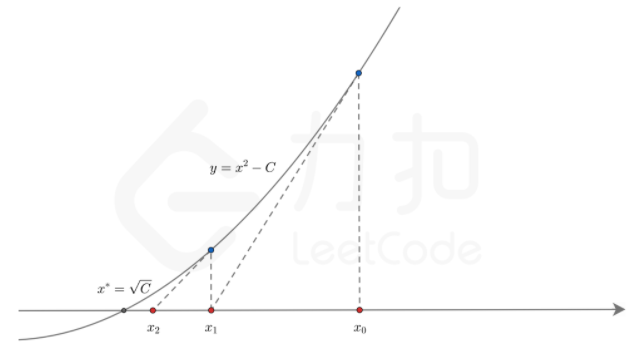
比如求平方根: ,可以转为求
这个方程的根,就可以用牛顿-拉弗森方法求。求平方根用牛顿-拉弗森方法是安全的,没有我之前说的那么多坑。不过我看了有一些工程师写的代码,就有点滥用牛顿-拉弗森方法了,没有从数学角度进行更多的考虑。
数学的魅力就在于,哪怕18世纪就证明了五次及以上多项式方程没有根式解,随着时间的发展,这个证明并不会被推翻,不像技术一样会日新月异。所以牛顿-拉弗森方法仍然在计算机学科中被广泛使用。
文章最新版本在(有可能会有后续更新):如何通俗地理解牛顿迭代法?