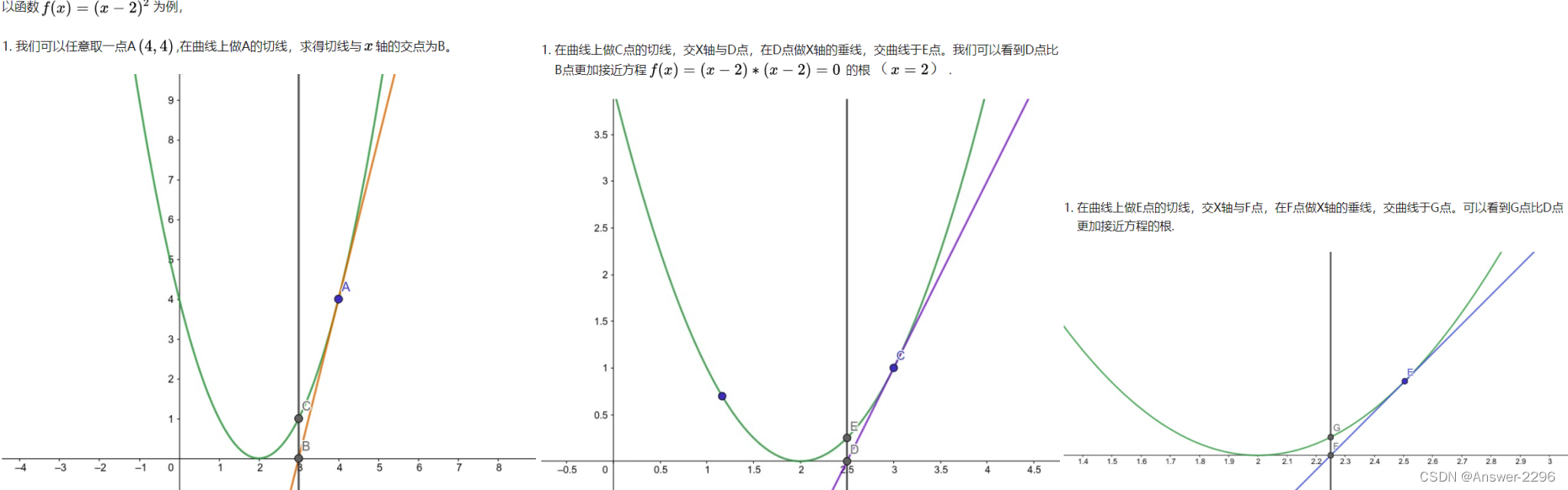
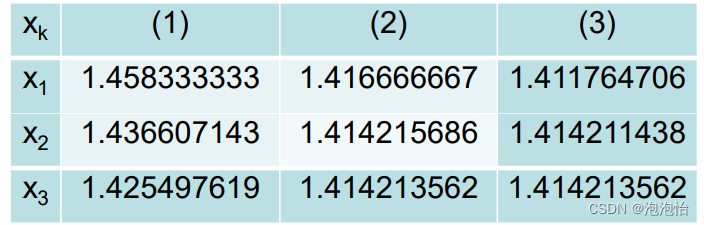
使用牛顿迭代法求解方程
尽管通过因式分解和利用求根公式可以很方便的得出多项式方程的根,但大多数时候这个多项式的次数都很高,计算将变得非常复杂,因此,我们必须转向一些近似解法。
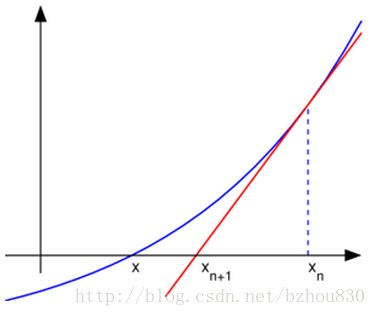
牛顿迭代法是其中最好的方法之一。从根本上说,牛顿迭代法通过一系列的迭代操作使得到的结果不断逼近方程的实根。
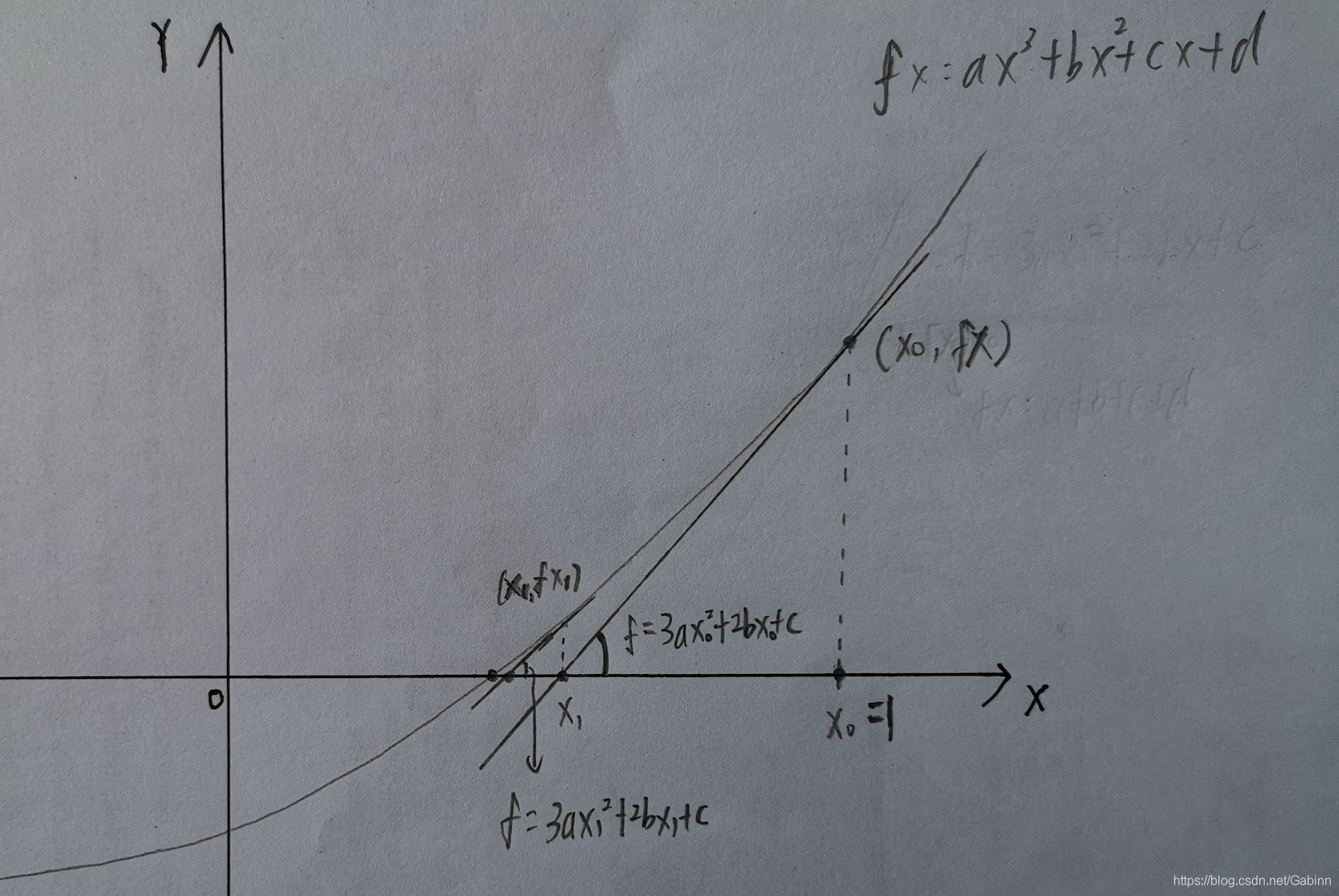
首先,要选择一个初始值x=x0,使得该初始值接近实根的值。然后,迭代计算如下的公式:
xi+1 = xi - f(xi) / f '(xi)
直到xi+1达到一个满意的近似结果为止。在这个公式中,f(x)是要求解的多项式方程,而f '(x)是f(x)的导数。
多项式求导
多项式求导是微积分的基础,现在让我们来看看针对多项式求导的公式化描述。
要计算出多项式的求导结果,只需要对多项式的每一项套用如下两个公式:
d/dx * k = 0, d/dx *kxr = krx r-1
这里的k是为常数,r是有理数,x是未知数。符号d/dx表示求导,其中x是多项式中的变量。
对于多项式中的每一常数项,套用第一个公式;否则,就用第二个公式。假设有如下函数:
f(x) = x3 + 5x2 +3x +4
要得到求导后的结果f '(x),对该多项式的前三项套用第二个公式,最后一项套用第1个公式,得到结果如下:
f '(x) = 1 * 3x(3-1) + 5 * 2x(2-1) + 3 * 1x(1-1) + 0 = 3x2 + 10x +3
有时候也有必要进行高阶求导,即导数的导数。比如,f(x)的2阶求导可记为f ''(x),它是对f '(x)的求导结果。同理,f(x)的3阶求导可记为f '''(x),这是对f ''(x)的求导结果,以此类推。因此,在前面的例子中,如果要计算f(x)的2阶导数的话,我们按照如下的方式对f '(x)求导即可:
f ''(x) = 3 * 2x(2-1) + 10 * 1x(1-1) + 0 =6x +10
理解1阶和2阶导数
理解1阶和2阶导数的意义,是正确使用牛顿迭代法非常重要的一点。
f(x)在点x=x0处的1阶导数表示函数f(x)在点x0处的斜率。
1阶导数决定函数f(x)是递增的(从左到右上升)还是递减的(从左右到下降)。如果求导结果为正,f(x)就是递增的;而如果求导结果为负,f(x)就是递减的;如果求导结果为0,则f(x)即不是递增的也不是递减的。求导结果的大小表示f(x)递增或递减的速率。如下图所示,阴影部分表示函数的递增区间,因此这些区域里函数的1阶导数都为正值。而中间穿过横轴的部分里函数是单调递减的,因此这个区域内的1阶导数所表示的斜率都为负值。
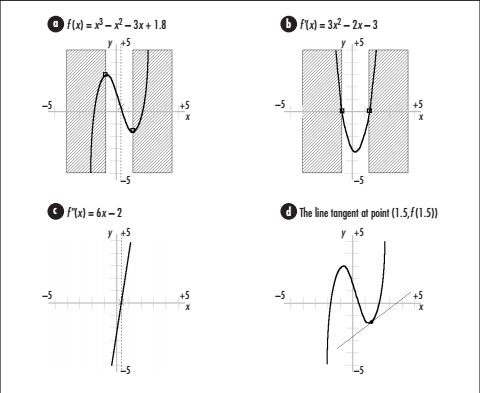
图:函数f(x)的1阶和2阶导数的意义
f(x)在点x=x0处的2阶导数表示函数在该点处的凹凸性,也就是说函数图像是向上凸的还是向下凹的。
2阶导数值的大小表示函数图像的凹凸程度。在上图的a和c中,虚线表示函数凹凸性发生改变的位置(曲线上凸部和下凹部的分界点,也称为拐点),拐点必然是2阶导函数与x轴的交点。
另一种表示函数f(x)在某点x=c处的导数的方法是:按照点斜式表示出与f(x)相切于点c的直线方程。直线点斜式方程可写作:
y - f(c) = f ' (c)(x-c)
因此,如果f(x) = x3 - x2 - 3x + 1.8如上图a所示,那么与f(x)相切于c=1.5的直线方程就可以表示为:
y - ((1.5)3 - (1.5)2 - 3*1.5 + 1.8) = (3 * 1.52 -2 * 1.5 - 3)(x - 1.5)
y + 1.575 = 0.75(x - 1.5)
上图d中画出了这条切线。
为牛顿迭代法确定迭代初始值
牛顿迭代法中至关重要的一点是选出一个合适的初始迭代值x0。为了使牛顿迭代法能够收敛至我们要求的根,初始迭代值必须要足够接近于所求的根。下面有两条规则必须满足:
1、为x0确定一个区间[a,b],使得该区间内有且只有一个根存在。为了实现这个目的,需要选择两个值a和b,使得f(a)和f(b)的符号不同,且f '(x)的符号不会改变。如果f(a)和f(b)有不同的符号,则表示该区间内至少存在一个根。如果f '(x)的符号在区间[a,b]上不变,则可确定该区间内只包含一个根,因为该函数在此区间内只可能单调的递增或递减。
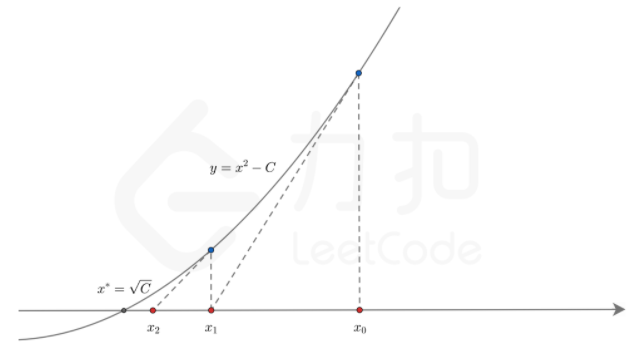
2、使x0=a或x0=b,这样f(x0)的符号就和f ''(x)在区间[a,b]上的符号相同。这也说明了f ''(x)在区间[a,b]上的符号不会改变。回顾一下,f(x)的2次导数表示函数的凹凸性,如果f ''(x)的符号不变,则f(x0)就和f ''(x)拥有相同的符号。每经过一次牛顿迭代,就会在区间[a,b]上逐步逼近于根。如下图。
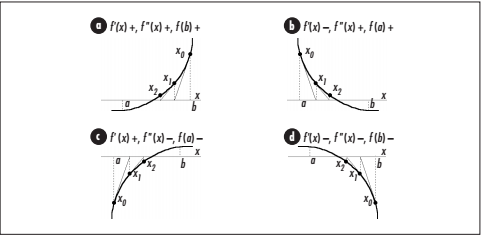
图:牛顿迭代法的收敛
在上图的4个部分中,f(x)以粗实线表示,a和b都表示为垂直的虚线。如果f(a)满足前面给出的规定,则从a开始迭代,且切线会朝着根收敛的方向倾斜。如果f(b)满足前面给定的规定,迭代就从b开始。且切线也会朝着根收敛的方向倾斜。
牛顿迭代法的工作过程
假设我们想找出方程f(x) = x3 - x2 - 3x + 1.8的根。根据函数图像(如下图),该方程会有三个根:一个在区间[-2,-1],另一个在区间[0,-1],第三个在区间[2,3]。一旦知道了方程的根的个数以及它们所在的区间,就根据上面的要求对每个区间做测试,以此挑出一个初始迭代值。要实现这一点,首先得知道如下信息:
f(x) = x3 - x2 - 3x + 1.8,f '(x) = 3x2 - 2x - 3,f ''(x) = 6x - 2
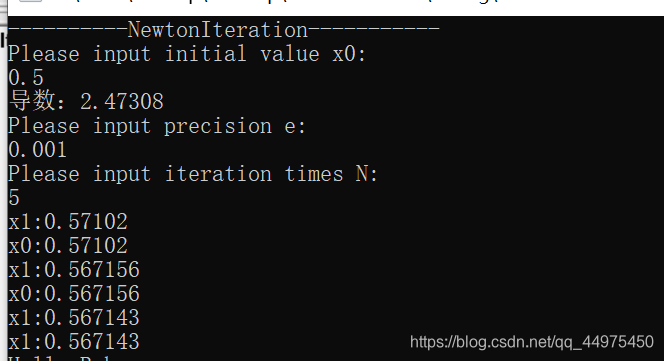
利用这些信息,我们发现[-1,-2]满足第一个要求,因为f(-2) = -4.2,f(-1) = 2.8,且f '(x)在该区间内没有改变符号(一直都是正的)。到这,我们知道在区间[-2,-1]内有且只有一个根。现在需要检查是否满足第二个要求,我们发现f ''(x)在区间上并没有改变过符号(一直都是负的)。因为f(-2)=-4.2也是负值,所以选择x0 = -2作为迭代的初始值。下图展示了在该区间内迭代计算根的过程,其精度达到了0.0001。只经过5次迭代就得到了这个近似值。
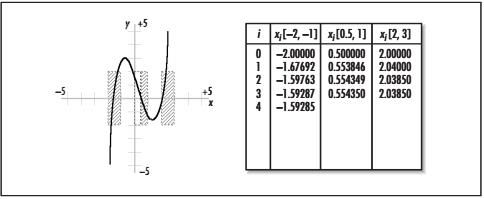
图:计算方程f(x) = x3 - x2 - 3x + 1.8 = 0的3个根的近似值,精确度0.0001
再来看看如何求出区间[0,1]上的根。我们能够看到第一个要求在该区间上是能够满足的,但是在该区间的f''(x)的符号并不是不变的,因此这个区间不能满足第二个要求。我们怀疑这个根更接近于1而不是0,因此我们接下来尝试使用区间[0.5,1],这个可以解决不满足第二个要求的问题了。f(0.5) = 0.175,f(1) = -1.2,f '(x)在这个区间内都是负值,因此第一个要求可以满足。要完成第二个要求让初始值x0 = 0.5,因为f(0.5)=0.175为正值,且同f ''(x)在区间[0.5,1]上的符号相同。上图也展示了在区间[0.5,1]上迭代计算根的过程,其精度达到了0.0001。最后用了4次迭代就达到了根的近似值。计算第3个根的过程也与此类似。
方程求解的接口定义
root
int root(double (*f)(double x), double (*g)(double x), double *x, int *n, double delta)
复杂度: O(n),这里n表示调用者希望进行的最大迭代次数。
方程求解的实现与分析
求解形如f(x) = 0的方程,本质上就是要找出它的根。函数root采用牛顿迭代法以给定的初始迭代值开始逐次迭代逼近,从而找到实际根。
root函数包含单个循环,该循环采用牛顿迭代公式来连续计算根的近似值。在本节给出的实现中,f就代表需要求解的方程,g代表f的导函数。每一次迭代,我们要判断当前得到的近似值是否满足需求。如果当前得到的近似值与前一轮迭代得到的近似值之差小于delta所指定的值,则认为当前的近似值满足要求。如果经过n次迭代后还是没有找到满足要求的近似根,则从函数中返回-1以表示没有找到近似根。
root函数的时间复杂度为O(n),这里n表示调用者希望进行迭代的最大次数。最坏情况是当没有找到所需要的近似根时,此时一共会进行n次迭代。
文转自:http://www.ylsjwang.com/mingxing/13.html
示例:方程求解的实现
#include <math.h>
#include "nummeths.h"
int root(double (*f)(double x), double (*g)(double x), double *x, int *n, double delta)
{
int satisfied,i;
i = 0;
satisfied = 0;
while(!satisfied && i+1 < *n)
{
/*x的下一个迭代值*/
x[i+1] = x[i] - (f(x[i]) / g(x[i]));
/*确定是否获得期望的近似值*/
if(fabs(x[i+1] - x[i]) < delta)
satisfied = 1;
/*为下一次迭代做准备*/
i++;
}
/*即使没有迭代,也表明一个值已经存储在x中*/
if (i==0)
*n=1;
else
*n=i+1;
/*找到实根返回0,或者达到最大迭代次数仍没有找到实根,返回-1*/
if(satisfied)
return 0;
else
return -1;
}
尽管通过因式分解和利用求根公式可以很方便的得出多项式方程的根,但大多数时候这个多项式的次数都很高,计算将变得非常复杂,因此,我们必须转向一些近似解法。
牛顿迭代法是其中最好的方法之一。从根本上说,牛顿迭代法通过一系列的迭代操作使得到的结果不断逼近方程的实根。
首先,要选择一个初始值x=x0,使得该初始值接近实根的值。然后,迭代计算如下的公式:
xi+1 = xi - f(xi) / f '(xi)
直到xi+1达到一个满意的近似结果为止。在这个公式中,f(x)是要求解的多项式方程,而f '(x)是f(x)的导数。
多项式求导
多项式求导是微积分的基础,现在让我们来看看针对多项式求导的公式化描述。
要计算出多项式的求导结果,只需要对多项式的每一项套用如下两个公式:
d/dx * k = 0, d/dx *kxr = krx r-1
这里的k是为常数,r是有理数,x是未知数。符号d/dx表示求导,其中x是多项式中的变量。
对于多项式中的每一常数项,套用第一个公式;否则,就用第二个公式。假设有如下函数:
f(x) = x3 + 5x2 +3x +4
要得到求导后的结果f '(x),对该多项式的前三项套用第二个公式,最后一项套用第1个公式,得到结果如下:
f '(x) = 1 * 3x(3-1) + 5 * 2x(2-1) + 3 * 1x(1-1) + 0 = 3x2 + 10x +3
有时候也有必要进行高阶求导,即导数的导数。比如,f(x)的2阶求导可记为f ''(x),它是对f '(x)的求导结果。同理,f(x)的3阶求导可记为f '''(x),这是对f ''(x)的求导结果,以此类推。因此,在前面的例子中,如果要计算f(x)的2阶导数的话,我们按照如下的方式对f '(x)求导即可:
f ''(x) = 3 * 2x(2-1) + 10 * 1x(1-1) + 0 =6x +10
理解1阶和2阶导数
理解1阶和2阶导数的意义,是正确使用牛顿迭代法非常重要的一点。
f(x)在点x=x0处的1阶导数表示函数f(x)在点x0处的斜率。
1阶导数决定函数f(x)是递增的(从左到右上升)还是递减的(从左右到下降)。如果求导结果为正,f(x)就是递增的;而如果求导结果为负,f(x)就是递减的;如果求导结果为0,则f(x)即不是递增的也不是递减的。求导结果的大小表示f(x)递增或递减的速率。如下图所示,阴影部分表示函数的递增区间,因此这些区域里函数的1阶导数都为正值。而中间穿过横轴的部分里函数是单调递减的,因此这个区域内的1阶导数所表示的斜率都为负值。

图:函数f(x)的1阶和2阶导数的意义
f(x)在点x=x0处的2阶导数表示函数在该点处的凹凸性,也就是说函数图像是向上凸的还是向下凹的。
2阶导数值的大小表示函数图像的凹凸程度。在上图的a和c中,虚线表示函数凹凸性发生改变的位置(曲线上凸部和下凹部的分界点,也称为拐点),拐点必然是2阶导函数与x轴的交点。
另一种表示函数f(x)在某点x=c处的导数的方法是:按照点斜式表示出与f(x)相切于点c的直线方程。直线点斜式方程可写作:
y - f(c) = f ' (c)(x-c)
因此,如果f(x) = x3 - x2 - 3x + 1.8如上图a所示,那么与f(x)相切于c=1.5的直线方程就可以表示为:
y - ((1.5)3 - (1.5)2 - 3*1.5 + 1.8) = (3 * 1.52 -2 * 1.5 - 3)(x - 1.5)
y + 1.575 = 0.75(x - 1.5)
上图d中画出了这条切线。
为牛顿迭代法确定迭代初始值
牛顿迭代法中至关重要的一点是选出一个合适的初始迭代值x0。为了使牛顿迭代法能够收敛至我们要求的根,初始迭代值必须要足够接近于所求的根。下面有两条规则必须满足:
1、为x0确定一个区间[a,b],使得该区间内有且只有一个根存在。为了实现这个目的,需要选择两个值a和b,使得f(a)和f(b)的符号不同,且f '(x)的符号不会改变。如果f(a)和f(b)有不同的符号,则表示该区间内至少存在一个根。如果f '(x)的符号在区间[a,b]上不变,则可确定该区间内只包含一个根,因为该函数在此区间内只可能单调的递增或递减。
2、使x0=a或x0=b,这样f(x0)的符号就和f ''(x)在区间[a,b]上的符号相同。这也说明了f ''(x)在区间[a,b]上的符号不会改变。回顾一下,f(x)的2次导数表示函数的凹凸性,如果f ''(x)的符号不变,则f(x0)就和f ''(x)拥有相同的符号。每经过一次牛顿迭代,就会在区间[a,b]上逐步逼近于根。如下图。

图:牛顿迭代法的收敛
在上图的4个部分中,f(x)以粗实线表示,a和b都表示为垂直的虚线。如果f(a)满足前面给出的规定,则从a开始迭代,且切线会朝着根收敛的方向倾斜。如果f(b)满足前面给定的规定,迭代就从b开始。且切线也会朝着根收敛的方向倾斜。
牛顿迭代法的工作过程
假设我们想找出方程f(x) = x3 - x2 - 3x + 1.8的根。根据函数图像(如下图),该方程会有三个根:一个在区间[-2,-1],另一个在区间[0,-1],第三个在区间[2,3]。一旦知道了方程的根的个数以及它们所在的区间,就根据上面的要求对每个区间做测试,以此挑出一个初始迭代值。要实现这一点,首先得知道如下信息:
f(x) = x3 - x2 - 3x + 1.8,f '(x) = 3x2 - 2x - 3,f ''(x) = 6x - 2
利用这些信息,我们发现[-1,-2]满足第一个要求,因为f(-2) = -4.2,f(-1) = 2.8,且f '(x)在该区间内没有改变符号(一直都是正的)。到这,我们知道在区间[-2,-1]内有且只有一个根。现在需要检查是否满足第二个要求,我们发现f ''(x)在区间上并没有改变过符号(一直都是负的)。因为f(-2)=-4.2也是负值,所以选择x0 = -2作为迭代的初始值。下图展示了在该区间内迭代计算根的过程,其精度达到了0.0001。只经过5次迭代就得到了这个近似值。

图:计算方程f(x) = x3 - x2 - 3x + 1.8 = 0的3个根的近似值,精确度0.0001
再来看看如何求出区间[0,1]上的根。我们能够看到第一个要求在该区间上是能够满足的,但是在该区间的f''(x)的符号并不是不变的,因此这个区间不能满足第二个要求。我们怀疑这个根更接近于1而不是0,因此我们接下来尝试使用区间[0.5,1],这个可以解决不满足第二个要求的问题了。f(0.5) = 0.175,f(1) = -1.2,f '(x)在这个区间内都是负值,因此第一个要求可以满足。要完成第二个要求让初始值x0 = 0.5,因为f(0.5)=0.175为正值,且同f ''(x)在区间[0.5,1]上的符号相同。上图也展示了在区间[0.5,1]上迭代计算根的过程,其精度达到了0.0001。最后用了4次迭代就达到了根的近似值。计算第3个根的过程也与此类似。
方程求解的接口定义
root
int root(double (*f)(double x), double (*g)(double x), double *x, int *n, double delta)
返回值:如果找到了根返回0;否则返回-1。
描述:采用牛顿迭代法,根据给定的初始值来计算方程f的根。初始值由x[0]指定。函数f的导数由参数g指定。参数n代表迭代的最大次数。参数delta表示逐次逼近的差值,用该值来决定何时应该结束迭代。函数返回后,迭代过程中计算出的近似值都保存在数组x中,此时n代表数组x中的元素个数。由调用者负责管理同x相关联的存储空间。复杂度: O(n),这里n表示调用者希望进行的最大迭代次数。
方程求解的实现与分析
求解形如f(x) = 0的方程,本质上就是要找出它的根。函数root采用牛顿迭代法以给定的初始迭代值开始逐次迭代逼近,从而找到实际根。
root函数包含单个循环,该循环采用牛顿迭代公式来连续计算根的近似值。在本节给出的实现中,f就代表需要求解的方程,g代表f的导函数。每一次迭代,我们要判断当前得到的近似值是否满足需求。如果当前得到的近似值与前一轮迭代得到的近似值之差小于delta所指定的值,则认为当前的近似值满足要求。如果经过n次迭代后还是没有找到满足要求的近似根,则从函数中返回-1以表示没有找到近似根。
root函数的时间复杂度为O(n),这里n表示调用者希望进行迭代的最大次数。最坏情况是当没有找到所需要的近似根时,此时一共会进行n次迭代。
文转自:http://www.ylsjwang.com/mingxing/13.html
示例:方程求解的实现
#include <math.h>
#include "nummeths.h"
int root(double (*f)(double x), double (*g)(double x), double *x, int *n, double delta)
{
int satisfied,i;
i = 0;
satisfied = 0;
while(!satisfied && i+1 < *n)
{
/*x的下一个迭代值*/
x[i+1] = x[i] - (f(x[i]) / g(x[i]));
/*确定是否获得期望的近似值*/
if(fabs(x[i+1] - x[i]) < delta)
satisfied = 1;
/*为下一次迭代做准备*/
i++;
}
/*即使没有迭代,也表明一个值已经存储在x中*/
if (i==0)
*n=1;
else
*n=i+1;
/*找到实根返回0,或者达到最大迭代次数仍没有找到实根,返回-1*/
if(satisfied)
return 0;
else
return -1;
}