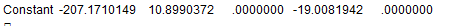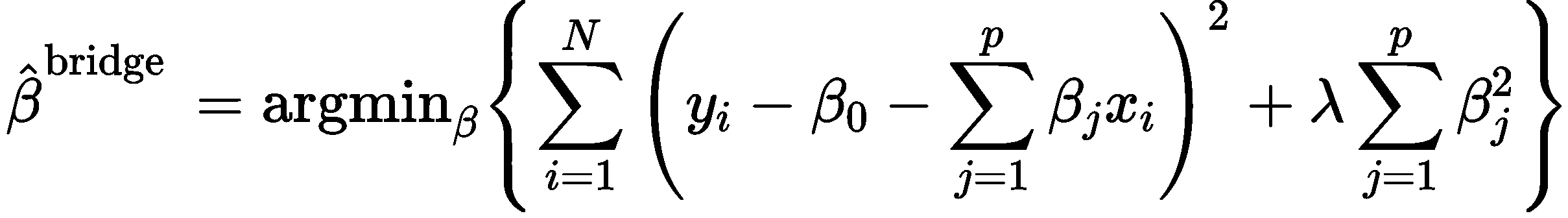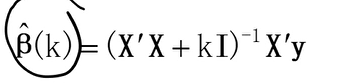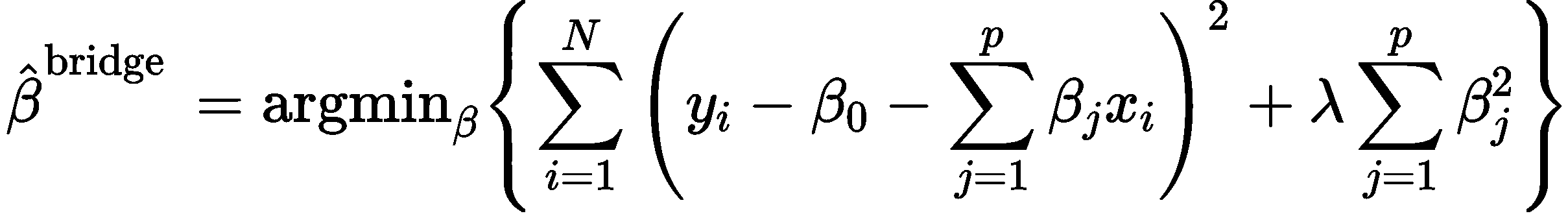机器学习学习笔记（13）----岭回归（Ridge回归）

article/2025/9/13 0:35:49

在《机器学习学习笔记（4）----线性回归的数学解析》，我们通过计算线性模型的损失函数的梯度，得到使得损失函数为最小值的 $\omega$ 的解析解，被称之为普通最小二乘法：

$\omega =(X^{T}X)^{-1}X^{T}y$ (1)

公式(1)能够求得的前提是 $X^{T}X$ 是满秩矩阵，这样才能计算得到它的逆矩阵。但是在很多情况下，矩阵不可逆。特别是当样本数m很大时，m >> n时，矩阵基本上是不可逆的，因为矩阵中出现大量线性相关的行向量的几率很高。这时，我们直接去算公式(1)是算不出来结果的。

为了解决这个问题，我们需要重新定义损失函数，在损失函数中引入范数项：

$J(\omega)=\frac{1}{2m}((y-X\omega ) ^{T}(y-X\omega ) + \lambda \left \|\omega \right \|_{p}^{p} )$ (2)

其中 $\lambda$ 是个正整数，当p=2时，就是指岭回归模型。

这样 $J(\omega )$ 的最小值就要求不仅是左边的部分要求得最小值，后面的范数项也要求得最小值。

对于岭回归模型，损失函数可以写成：

$J(\omega )=\frac{1}{2m}((y-X\omega)^{T}(y-X\omega)+\lambda \omega^{T}\omega$ （3）

注意：

$\frac{\partial(\omega ^{T} \omega)}{\partial\omega }=2\omega$ （4）

再根据我们前面在《机器学习学习笔记（4）----线性回归的数学解析》已经推导的结果，可得损失函数的梯度的表达式是：

$\bigtriangledown J(\omega )=\frac{1}{2m}(2X^{T}X\omega-2X^{T}y+2\lambda \omega) =\frac{1}{m}(X^{T}X\omega-X^{T}y+\lambda \omega)$ （5）

令 $\bigtriangledown J(\omega )=0$ ，则：

$X^{T}X\omega+\lambda \omega=X^{T}y$ (6)

$(X^{T}X+\lambda I) \omega=X^{T}y$ (7)，其中I是单位矩阵。

$\omega=(X^{T}X+\lambda I)^{-1} X^{T}y$ （8）

因为加入了 $\lambda I$ 项，通过调整 $\lambda$ 值， $X^{T}X+\lambda I$ 肯定可以调整为满秩矩阵，因此可以求得其逆矩阵。

接下来，我们用python实现一个岭回归算法(ridge.py):

import numpy as npclass RidgeRegression:def __init__(self, lambda_v=0.05):# 范数项的系数self.lambda_v = lambda_v# 模型参数w（训练时初始化）self.w = Nonedef _ridge(self, X, y):'''岭回归算法'''_,n = X.shapeI = np.identity(n)tmp = np.linalg.inv(np.matmul(X.T, X) + self.lambda_v*I)tmp = np.matmul(tmp, X.T)return np.matmul(tmp, y)def _preprocess_data_X(self, X):'''数据预处理'''# 扩展X，添加x0列并设置为1m, n = X.shapeX_ = np.empty((m, n+1))X_[:,0] = 1X_[:, 1:] = Xreturn X_def train(self, X_train, y_train):'''训练模型'''# 预处理X_train(添加x0列并设置为1)_X_train = self._preprocess_data_X(X_train)# 使用岭回归算法估算wself.w = self._ridge(_X_train, y_train)def predict(self, X):'''预测'''# 预处理X_train(添加x0列并设置为1)_X = self._preprocess_data_X(X)return np.matmul(_X, self.w)

_ridge函数，就是岭回归算法的实现。

使用红酒口感数据集，对上面的岭回归算法实现进行测试，红酒数据集的路径：https://archive.ics.uci.edu/ml/datasets/wine+quality，winequality-red.csv。

先加载数据集：

>>> import numpy as np
>>> data = np.genfromtxt('winequality-red.csv',delimiter=';',skip_header=True)
>>> X=data[:,:-1]
>>> y = data[:,-1]

然后创建模型：

>>> from ridge import RidgeRegression
>>> ridge_r = RidgeRegression()

然后，用train_test_split切分训练集和测试集：

>>> X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.3)

然后，做训练和预测：

>>> ridge_r.train(X_train, y_train)

>>> y_pred = ridge_r.predict(X_test)

使用均方误差来衡量回归模型的回归效果：

>>> mse = mean_squared_error(y_test, y_pred)
>>> mse
0.4284235160100709
>>> y_train_pred = ridge_r.predict(X_train)
>>> mse_train = mean_squared_error(y_train, y_train_pred)
>>> mse_train
0.41419102073144654

训练集的拟合效果好于测试集。

使用sklearn库中的岭回归模型进行训练和预测，并评估回归效果：

>>> from sklearn.linear_model import Ridge
>>> rg =Ridge(0.05, normalize=True)
>>> rg.fit(X_train, y_train)
Ridge(alpha=0.05, copy_X=True, fit_intercept=True, max_iter=None,
normalize=True, random_state=None, solver='auto', tol=0.001)
>>> y_pred=rg.predict(X_test)
>>> mse=mean_squared_error(y_test, y_pred)
>>> mse
0.4275656395927125
>>> y_train_pred = rg.predict(X_train)
>>> mse_train = mean_squared_error(y_train, y_train_pred)
>>> mse_train
0.4143351974898082

发现和我们示例的岭回归的效果差不多。

参考资料：

《机器学习：从公理到算法》

《机器学习算法》