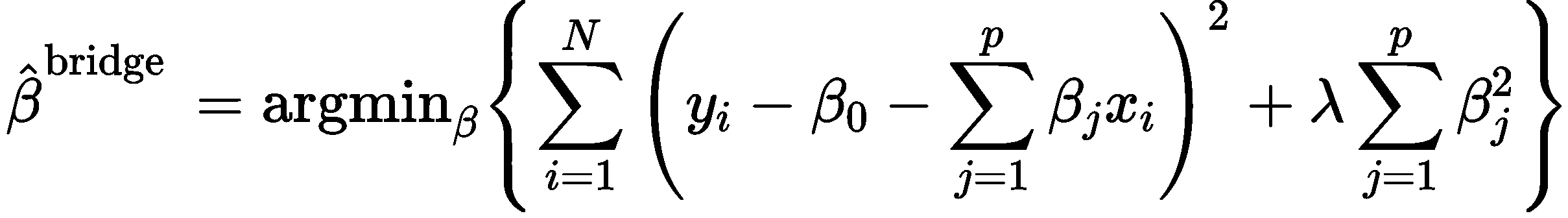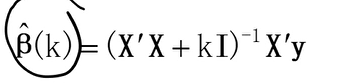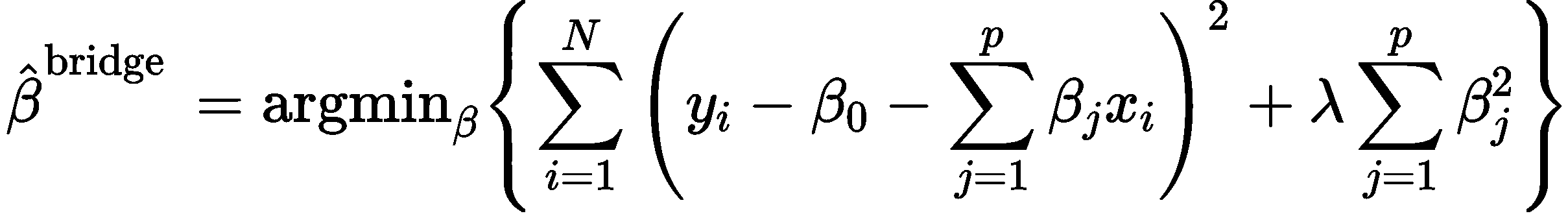岭回归(Ridge Regression)及实现

article/2025/9/13 0:46:53

岭回归(Ridge Regression)及实现

https://blog.csdn.net/google19890102/article/details/27228279

一、一般线性回归遇到的问题

在处理复杂的数据的回归问题时，普通的线性回归会遇到一些问题，主要表现在：

在处理复杂的数据的回归问题时，普通的线性回归会遇到一些问题，主要表现在：
预测精度：这里要处理好这样一对为题，即样本的数量和特征的数量
模型的解释能力：如果模型中的特征之间有相互关系，这样会增加模型的复杂程度，并且对整个模型的解释能力并没有提高，这时，我们就要进行特征选择。

预测精度：这里要处理好这样一对为题，即样本的数量和特征的数量
- $n\gg p$ 时，最小二乘回归会有较小的方差
- $n\approx p$ 时，容易产生过拟合
- $n$ 时，最小二乘回归得不到有意义的结果
模型的解释能力：如果模型中的特征之间有相互关系，这样会增加模型的复杂程度，并且对整个模型的解释能力并没有提高，这时，我们就要进行特征选择。

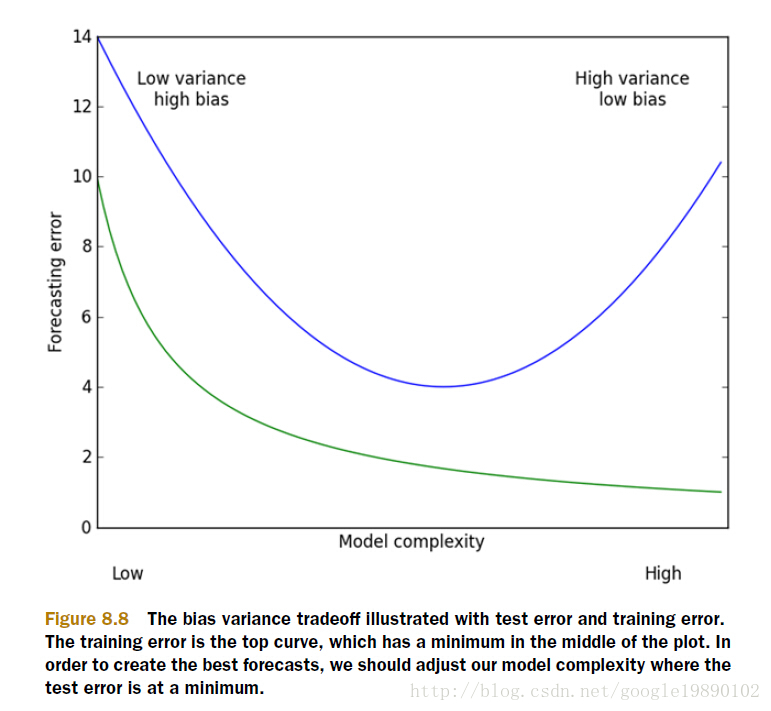
以上的这些问题，主要就是表现在模型的方差和偏差问题上，这样的关系可以通过下图说明：

（摘自：机器学习实战）

方差指的是模型之间的差异，而偏差指的是模型预测值和数据之间的差异。我们需要找到方差和偏差的折中。

二、岭回归的概念

在进行特征选择时，一般有三种方式：

子集选择
收缩方式(Shrinkage method)，又称为正则化(Regularization)。主要包括岭回归个lasso回归。
维数缩减

岭回归(Ridge Regression)是在平方误差的基础上增加正则项

$\sum_{i=1}^{n}\left ( y_i-\sum_{j=0}^{p}w_jx_{ij} \right )^2+\lambda \sum_{j=0}^{p}w^2_j$ , $\lambda > 0$

通过确定 $\lambda$ 的值可以使得在方差和偏差之间达到平衡：随着 $\lambda$ 的增大，模型方差减小而偏差增大。

对 $w$ 求导，结果为

$2X^T\left ( Y-XW \right )-2\lambda W$

令其为0，可求得 $w$ 的值：

$\hat{w}=\left ( X^TX+\lambda I \right )^{-1}X^TY$

三、实验的过程

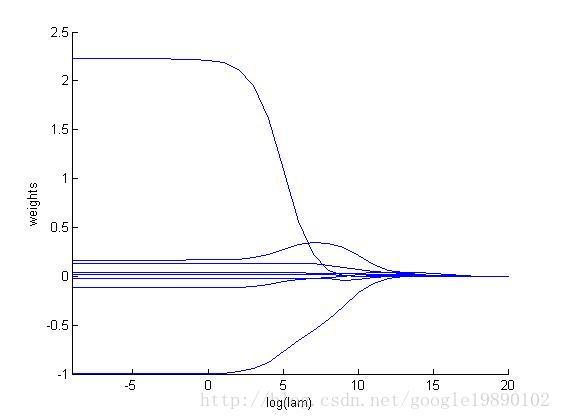
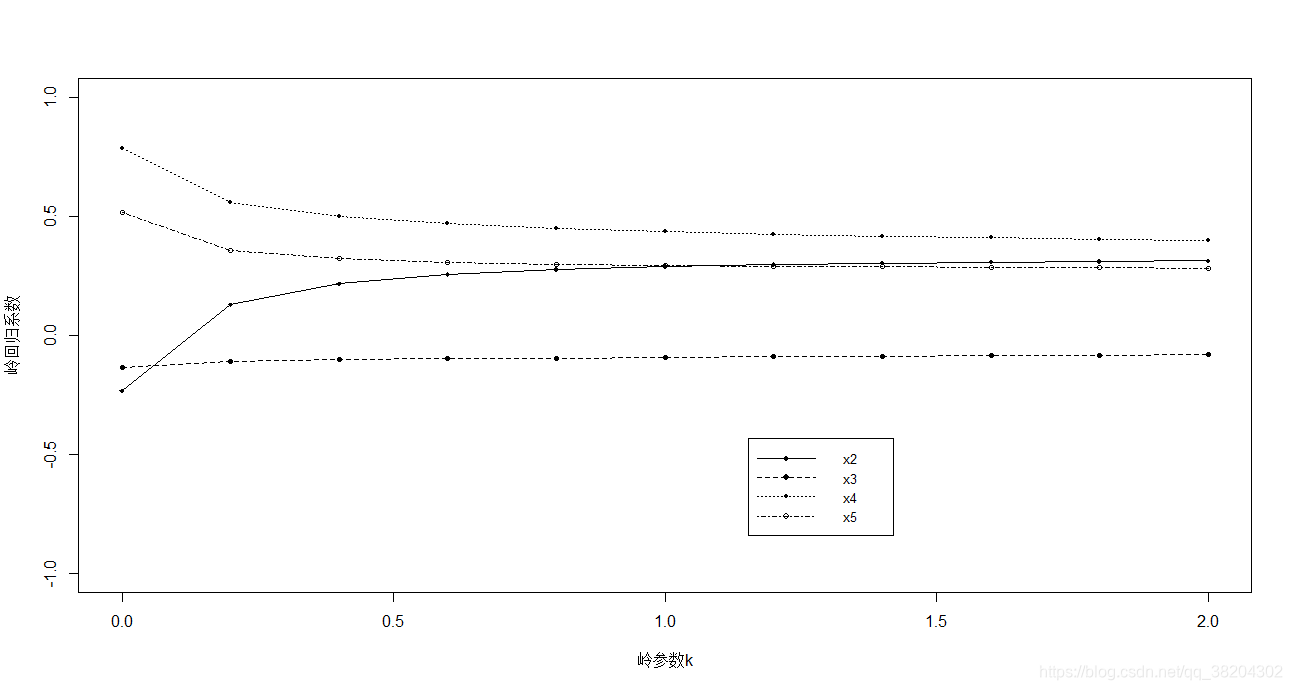
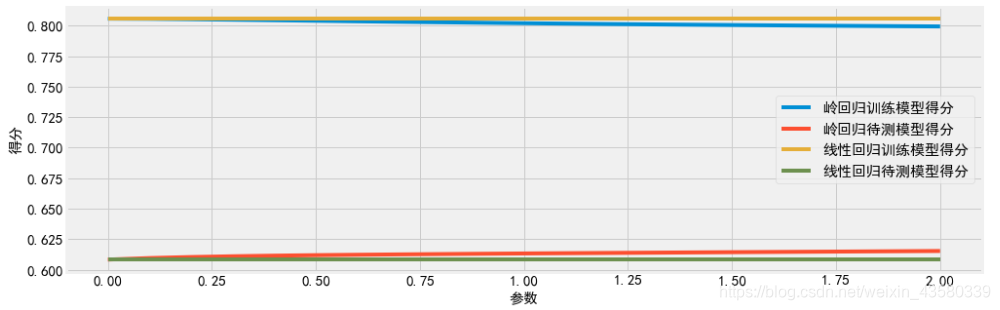
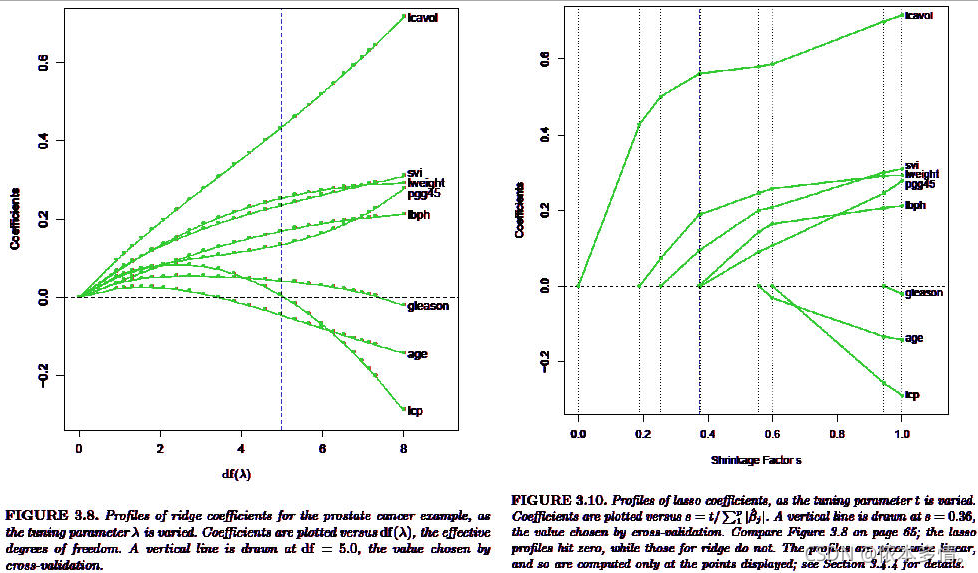
我们去探讨一下取不同的 $\lambda$ 对整个模型的影响。

MATLAB代码

主函数

%% 岭回归(Ridge Regression)

%导入数据
data = load(‘abalone.txt’);
[m,n] = size(data);

dataX = data(:,1:8);%特征
dataY = data(:,9);%标签

%标准化
yMeans = mean(dataY);
for i = 1:m
yMat(i,:) = dataY(i,:)-yMeans;
end

xMeans = mean(dataX);
xVars = var(dataX);
for i = 1:m
xMat(i,:) = (dataX(i,:) - xMeans)./xVars;
end

% 运算30次
testNum = 30;
weights = zeros(testNum, n-1);
for i = 1:testNum
w = ridgeRegression(xMat, yMat, exp(i-10));
weights(i,:) = w’;
end

% 画出随着参数lam
hold on
axis([-9 20 -1.0 2.5]);
xlabel log(lam);
ylabel weights;
for i = 1:n-1
x = -9:20;
y(1,:) = weights(:,i)’;
plot(x,y);
end

岭回归求回归系数的函数

function [ w ] = ridgeRegression( x, y, lam )xTx = x'*x;[m,n] = size(xTx);temp = xTx + eye(m,n)*lam;if det(temp) == 0disp('This matrix is singular, cannot do inverse');endw = temp^(-1)*x'*y;
end

https://www.jianshu.com/p/4880d476d40e

概述

对于普通最小二乘的参数估计问题，当模型的各项是相关时，最小二乘估计对于随机误差非常敏感，会产生很大的方差。一般来说，对于没有经过实验设计搜集到的数据，很容易出现这种多重共线性。而岭回归在最小二乘法的基础上通过对回归系数施加‘惩罚’来解决这些问题，具体来说，就是在偏差平方和函数中加上了一个l2正则项，通过正则项来调节参数，删除那些相关的项。岭回归 $y=Xw$ 的误差平方和函数 $\xi(x)$ 为: $\xi(x)=\|Xw-y\|_2^2+\alpha\|w\|_2^2$
其中， $\alpha\ge0$ 是控制系数伸缩量的参数，可以通过 $\alpha$ 的值使模型的方差和偏差达到平衡。随着 $\alpha$ 的增大，方差减小而偏差增大。

实际应用
Scitkit-learn使用Ridge()函数实现岭回归。

class sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver='auto', random_state=None)¶

Parameters
alpha:正则化系数，较大的值指定更强的正则化。
fit_intercept:是否计算模型的截距，默认为True，计算截距

normalize:在需要计算截距时，如果值为True，则变量x在进行回归之前先进行归一化（ $x = \frac{x-\bar x}{\|x\|_2}$ ）,如果需要进行标准化则normalize=False。若不计算截距，则忽略此参数。

copy_X:默认为True，将复制X；否则，X可能在计算中被覆盖。

max_iter:共轭梯度求解器的最大迭代次数。对于sparse_cg和lsqr,默认值由scipy.sparse.linalg确定。对于sag求解器，默认值为1000.
tol:float类型，指定计算精度。
solver：求解器{auto,svd,cholesky,lsqr,sparse_cg,sag,saga}

aotu:根据数据类型自动选择求解器
svd:使用X的奇异值分解计算岭系数。奇异矩阵比cholesky更稳定
cholesky:使用标准的scipy.linalg.solve函数获得收敛的系数
sparsr_cg:使用scipy.sparse.linalg.cg中的共轭梯度求解器。作为一种迭代算法，这个求解器比cholesky更适合大规模数据（设置tol和max_iter的可能性）
lsqr:使用专用的正则化最小二乘方法scipy.sparse.linalg.lsqr。
sag:使用随机平均梯度下降，saga使用其改进的，无偏见的版本，两种方法都使用迭代过程。

random_state:随机数生成器的种子。

Attributes

coef_:返回模型的估计系数。
intercept_:线性模型的独立项，一维情形下的截距。
n_iter:实际迭代次数。

Methods
fit(X,y):使用数据训练模型
get_params([deep=True]):返回函数LinearRegression()内部的参数值
predict(X):使用模型做预测
score(X，y):返回模型的拟合优度判定系数 $R^2$

$R^2$ 为回归平方和与总离差平方和的比值，介于0-1之间，越接近1模型的拟合效果越显著。

set_params(**params):设置函数LinearRegression()内部的参数。

实例

from sklearn.preprocessing import scale
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
from sklearn.datasets import load_boston
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
boston = load_boston()
X = scale(boston.data)
y = boston.target
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.8)
lmodel = Ridge(alpha=i,fit_intercept = True,solver = 'auto',copy_X=True)
lmodel.fit(X_train,y_train)

Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None,normalize=False, random_state=None, solver='auto', tol=0.001)

lmodel.coef_

array([-1.11125473,  0.89842868, -0.00522108,  0.65887304, -1.93970763,2.95928617, -0.13589642, -2.98057045,  2.57068677, -2.03507147,-2.02756142,  0.88785945, -3.39465369])

lmodel.intercept_

22.48662693222167

lmodel.score(X_train,y_train)

0.7818715197682596

lmodel.get_params()

{'alpha': 1.0,'copy_X': True,'fit_intercept': True,'max_iter': None,'normalize': False,'random_state': None,'solver': 'auto','tol': 0.001}

error = pow(lmodel.predict(X_test)-y_test,1)/len(X_test)
plt.figure(1,dpi = 100)
plt.scatter(np.arange(len(error)),error)
plt.ylabel('残差')
plt.title('残差图')