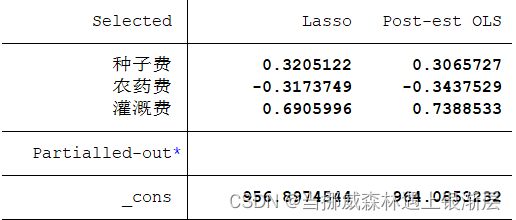
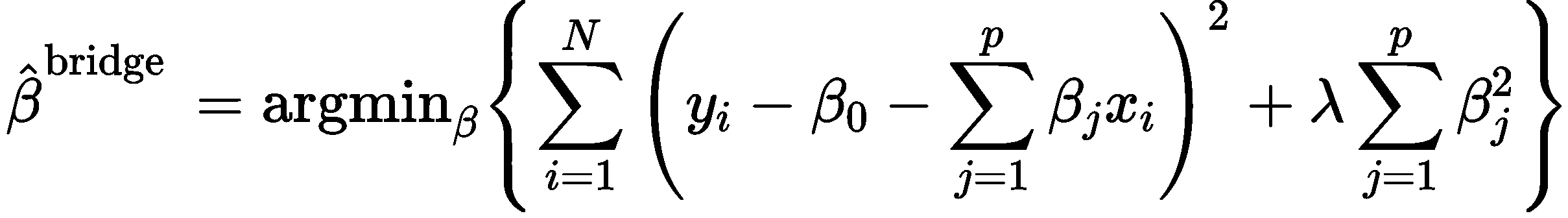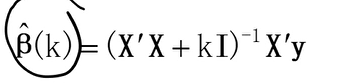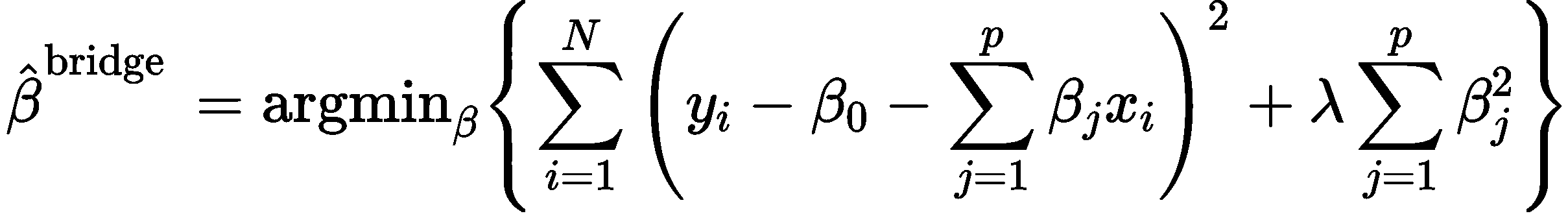本文是使用Python进行岭回归模型分析，消除多重共线性

一、岭回归原理

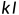自变量之间存在多重共线性，当时，加上一个正的常数矩阵(K>0)，岭回归估计定义公式：

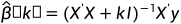（k为岭参数）

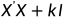的奇异程度比奇异程度小，其实就是减少了自变量之间的影响，消除多重共线性。其中X是标准化后的矩阵。

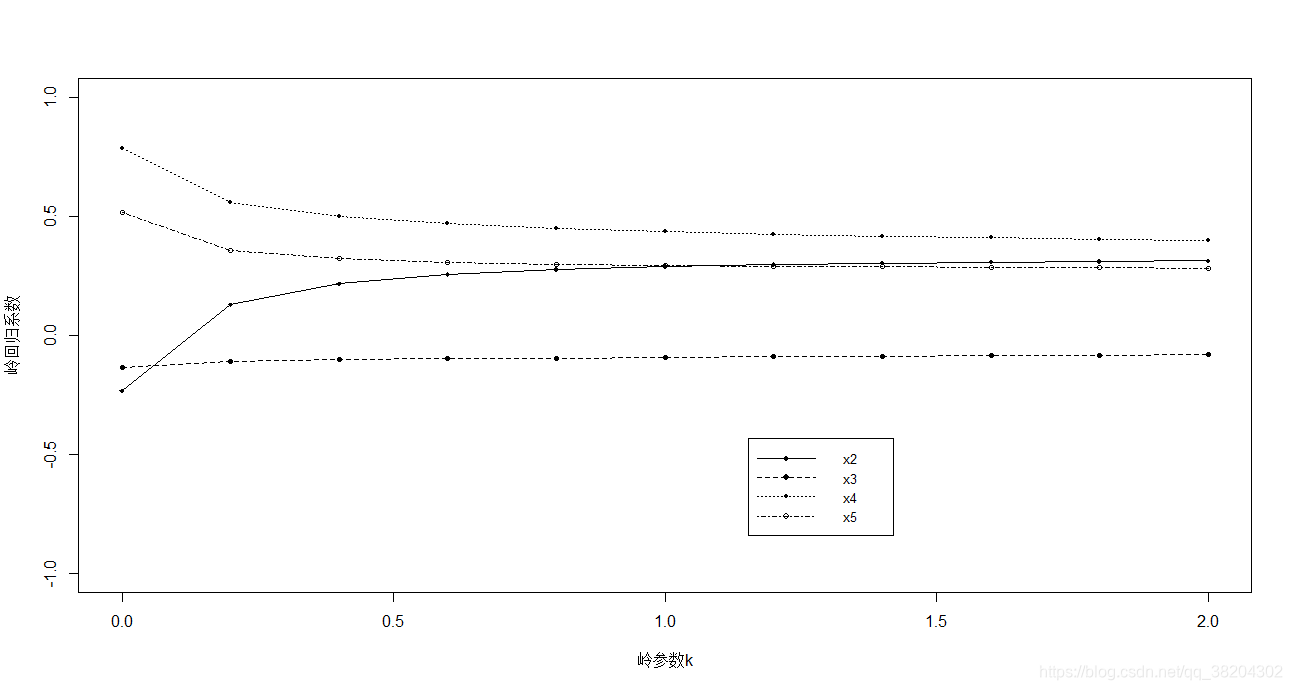
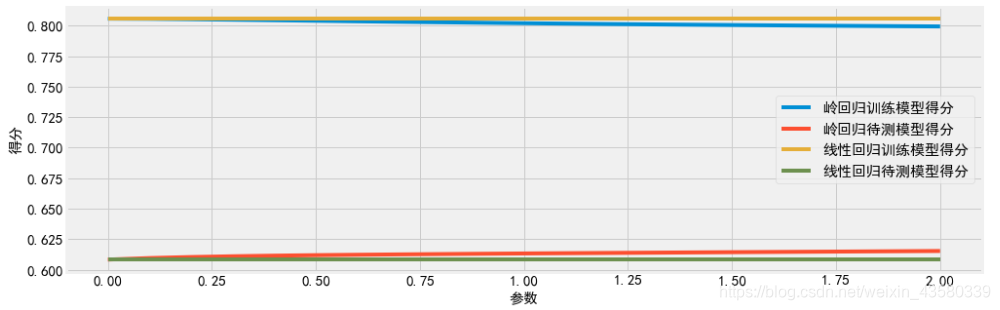
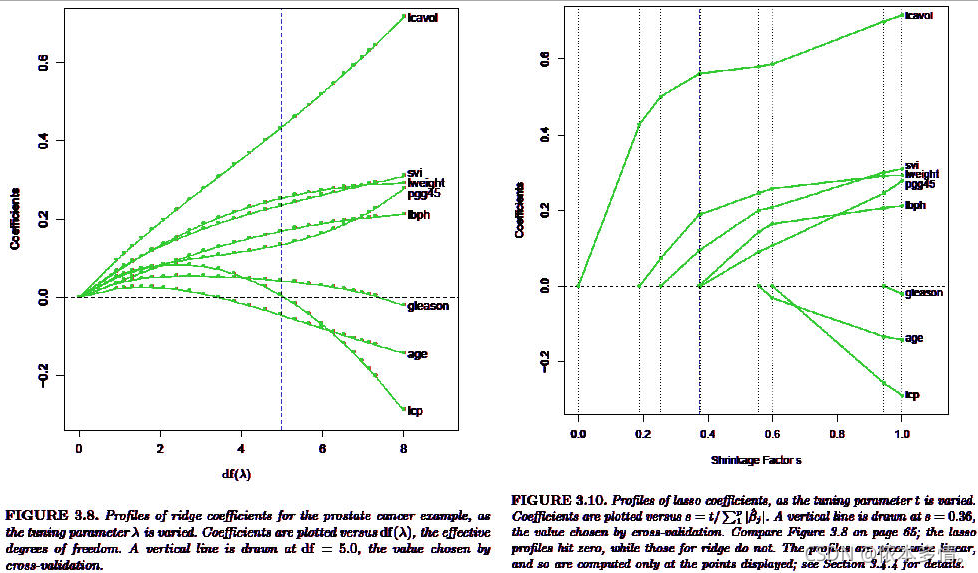
由于k是不确定的值，所以就会取一定k值范围，画岭迹图观察最佳的k值。

二、岭迹法

就是画出岭迹图，然后通过观察每个变量的岭迹变化趋势，剔除变化趋势大的自变量，使的岭回归估计变得平稳，由于这种观察具有较强的主观性，因此算是岭回归的一个不足，但是可以根据这个点进行一些其他的定性或者定量的分析。

三、多重共线性的判断

可以阅读这篇文章😘

https://blog.csdn.net/DL11007/article/details/129196843

四、代码实现

from sklearn.datasets import make_regression
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
import pandas as pd#读取数据
df = pd.read_csv('文件路径')  #这里数据以含有四个自变量为例#建模
result = smf.ols('y~x1+x2+x3+x4',data = df).fit()# 计算方差扩大因子（多重共线性判断）
VIFlist = []
for i in range(1, 3, 1):vif = variance_inflation_factor(result.model.exog, i)VIFlist.append(vif)
print(pd.Series(VIFlist))#岭回归处理（即原理部分）
eps = list(np.random.randn(25))  # 误差项，个数是由数据的条数决定
y = -1.1584 + 0.0547 * df['x1'] + 0.1341 * df['x2'] -0.0548 * df['x3']-0.0320* df['x4'] + eps
df['y'] = y  #覆盖原来的y值#岭回归模型
dfnorm = (df - df.mean()) / df.std() #标准化自变量矩阵
# 切片将x和y分开
Xnorm = dfnorm.iloc[:, 1:]
ynorm = df.iloc[:, 0]clf = Ridge()  #岭回归函数
coefs = []   #存放岭回归估计值
errors = []  #存放残差alphas = np.linspace(0.1, 30, 2000)  #步长为0.1， 取30个alpha值#遍历每个alpha值，计算出一系列的岭回归估计值
for a in alphas:clf.set_params(alpha=a)clf.fit(dfnorm, ynorm)coefs.append(clf.coef_)#画岭回归图
plt.subplot(111)  #创建一个画布
ax = plt.gca()   #gca()一个坐标轴的设置函数
ax.plot(alphas, coefs, label=list(Xnorm.keys()))   #画图
ax.legend(list(Xnorm.keys()), loc='best')  #设置图例
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization')
plt.axis('tight')
plt.show()#下面就是删除调变化趋势大的自变量，重复上面的所有的操作，直到一个最优的结果，然后确定k值

总结：

以上就是本次的内容，有疑问和错误的望指出，一起学习和进步！😘