1、作用
岭回归是一种专用于共线性数据分析的有偏估计回归方法,实质上是一种改良的最小二乘估计法,通过放弃最小二乘法的无偏性,以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法,对病态数据的拟合要强于最小二乘法。
2、输入输出描述
输入:自变量X至少一项或以上的定量变量或二分类定类变量,因变量Y要求为定量变量(若为定类变量,请使用逻辑回归)。
输出:模型检验优度的结果,自变量对因变量的线性关系等等。
3、学习网站
SPSSPRO-免费专业的在线数据分析平台
4、案例示例
案例:通过自变量(房间面积、楼层高度、房子单价、是否有电梯、周围学校数量、距地铁站位置)拟合预测因变量(房价),现在发现房子单价与楼层高度之间有着很强的共线性,VIF值高于20;不能使用常见的最小二乘法OLS回归分析,需要使用岭回归模型。
5、案例数据

岭回归案例数据
6、案例操作
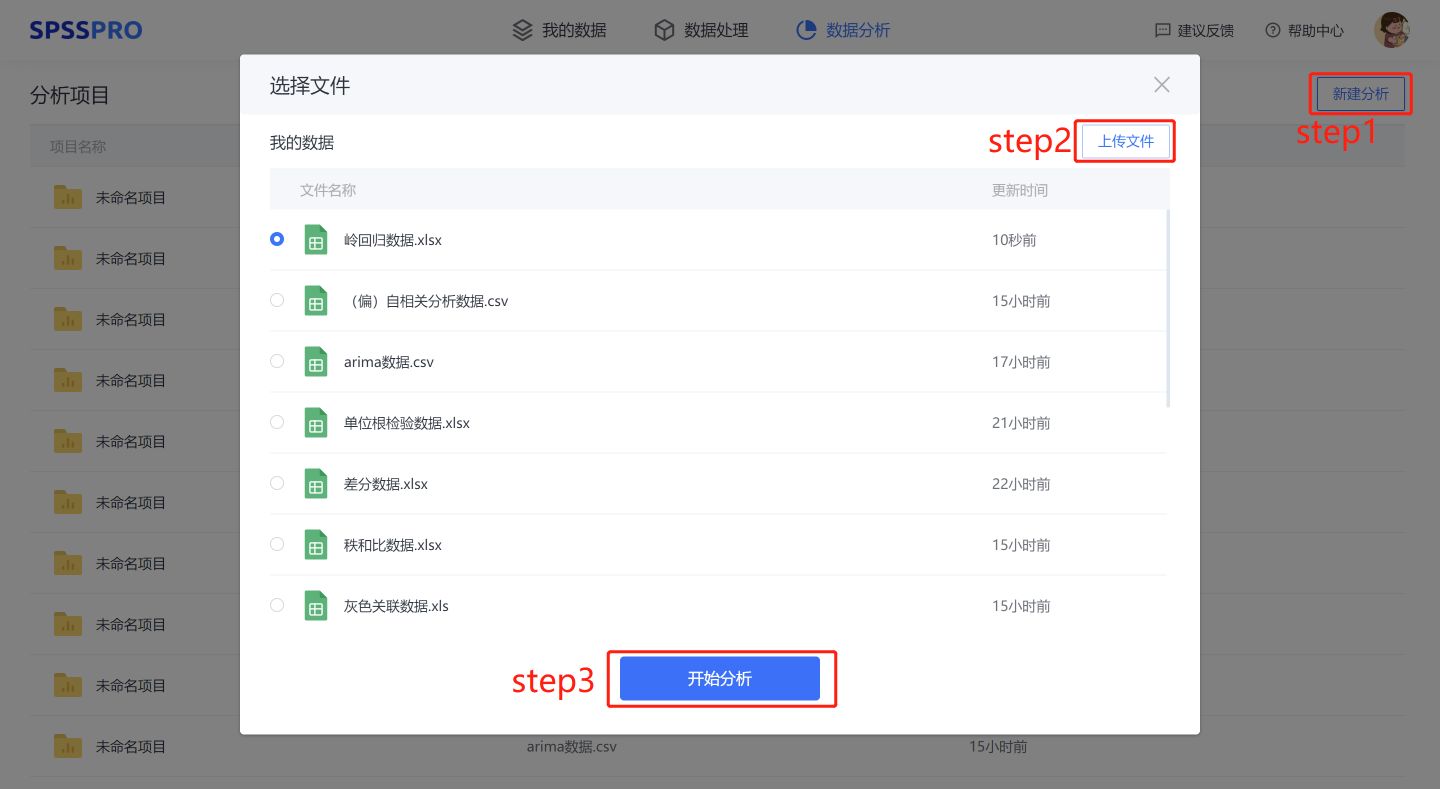
Step1:新建分析;
Step2:上传数据;
Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;
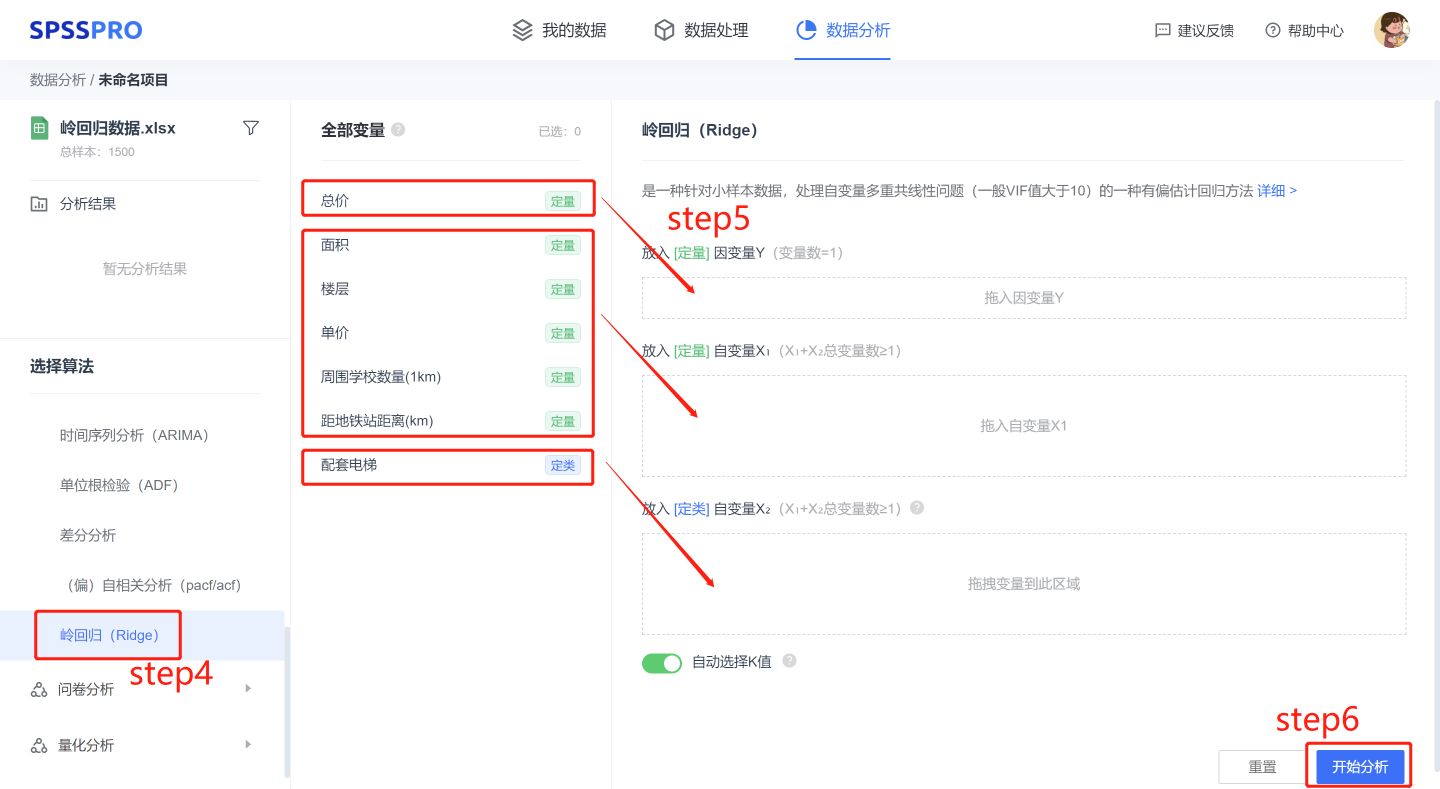
step4:选择【岭回归(Ridge)】;
step5:查看对应的数据数据格式,【岭回归(Ridge)】要求自变量X至少一项或以上的定量变量或二分类定类变量,因变量Y要求为定量变量。
step6:点击【开始分析】,完成全部操作。
7、输出结果分析
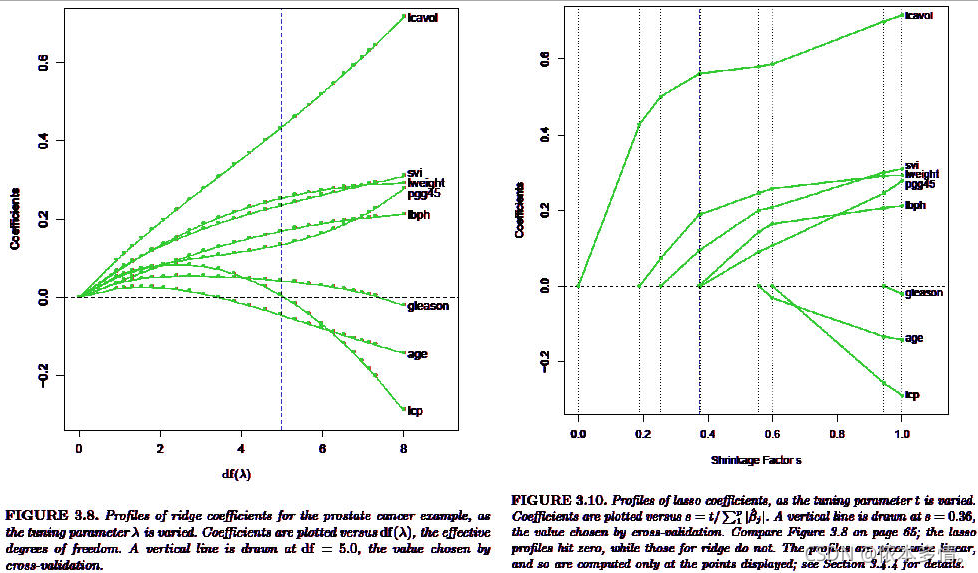
输出结果1:岭迹图
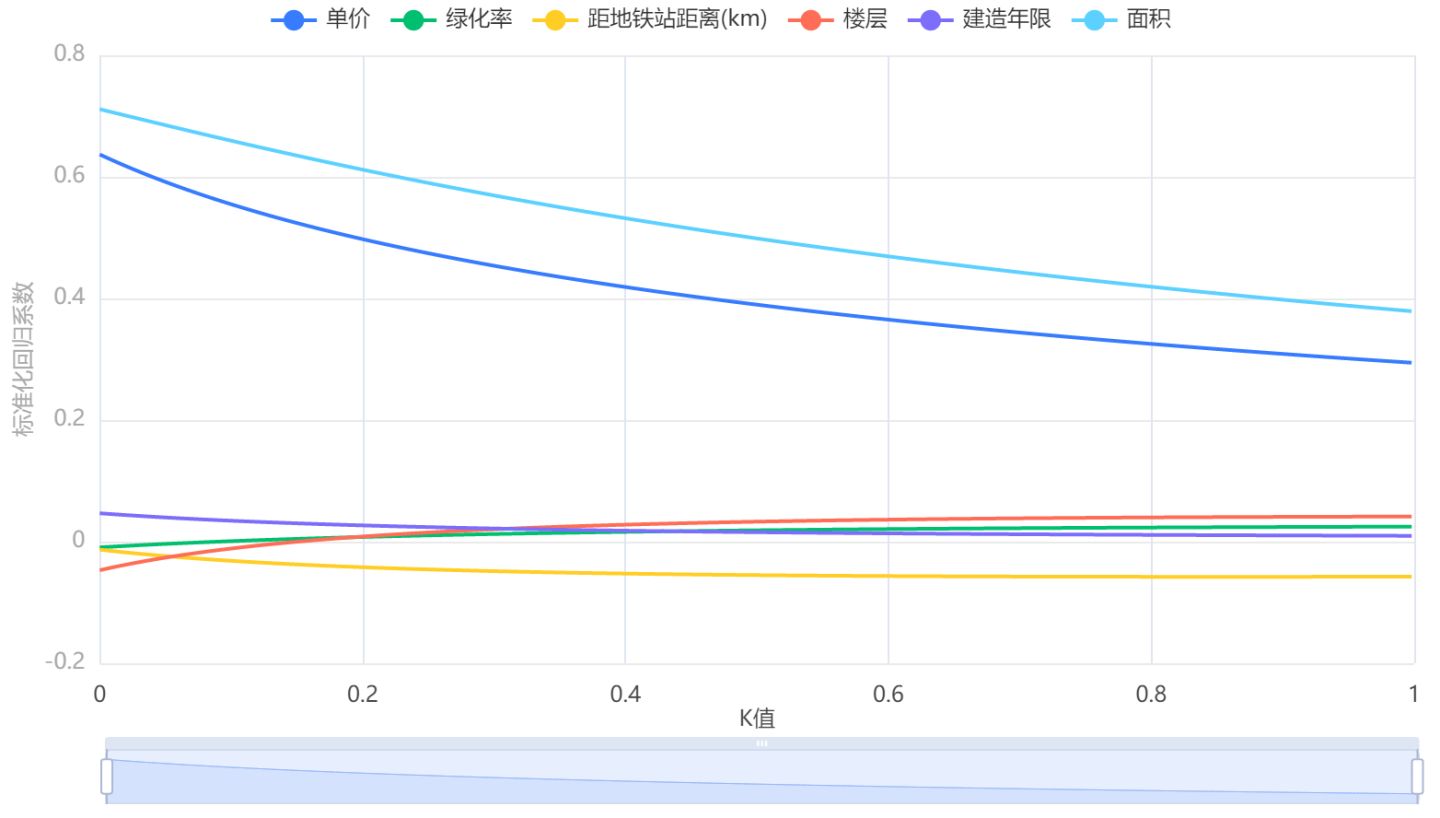
图表说明: 通过岭迹图,确定K值。K值的选择原则是各个自变量的标准化回归系数趋于稳定时的最小K值。但通过岭迹图分析方法确定的岭参数 k 在一定程度上存在主观人为性,psspro采用方差扩大因子法自动确定K=0.162。
输出结果2:岭回归分析结果
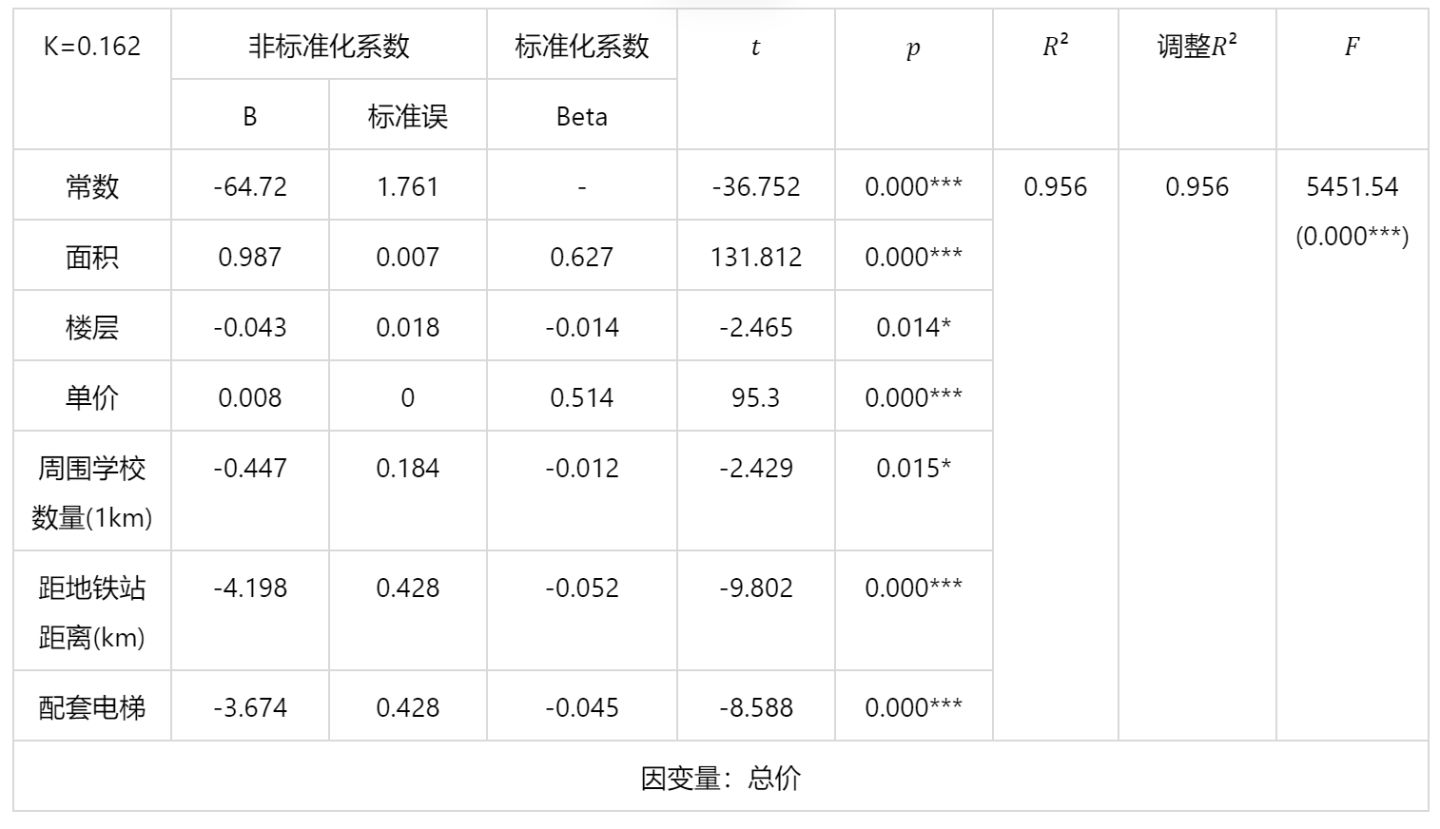
*p<0.05,**p<0.01,***p<0.001
图表说明:岭回归的结果显示:基于字段面积、楼层、单价、周围学校数量(1km)、距地铁站距离(km)、配套电梯回归模型显著性 值为0.000***,水平上呈现显著性,拒绝原假设,表明自变量与因变量之间存在着回归关系。同时,模型的拟合优度 ²为0.956,模型表现为较为较为优秀,因此模型基本满足要求。
模型的公式:
总价=-64.72+0.987 × 面积-0.043 × 楼层+0.008 × 单价-0.447 × 周围学校数量(1km)-4.198 × 距地铁站距离(km)-3.674 × 配套电梯r/&gt;<br/>输出结果3:模型路径图
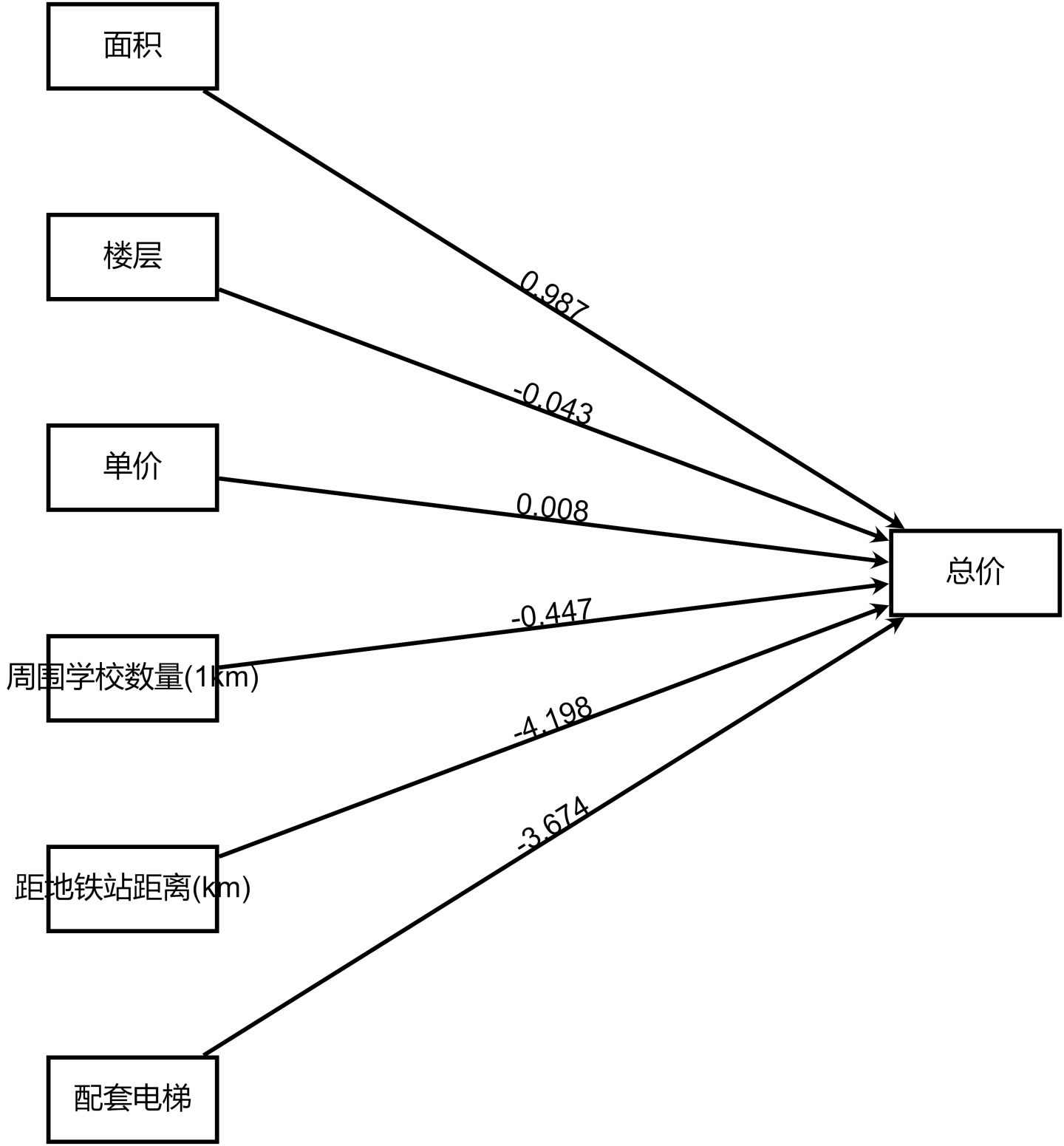
图表说明:上图以路径图形式展示了本次模型结果,主要包括模型的系数,用于分析模型的公式。
输出结果4:模型结果图
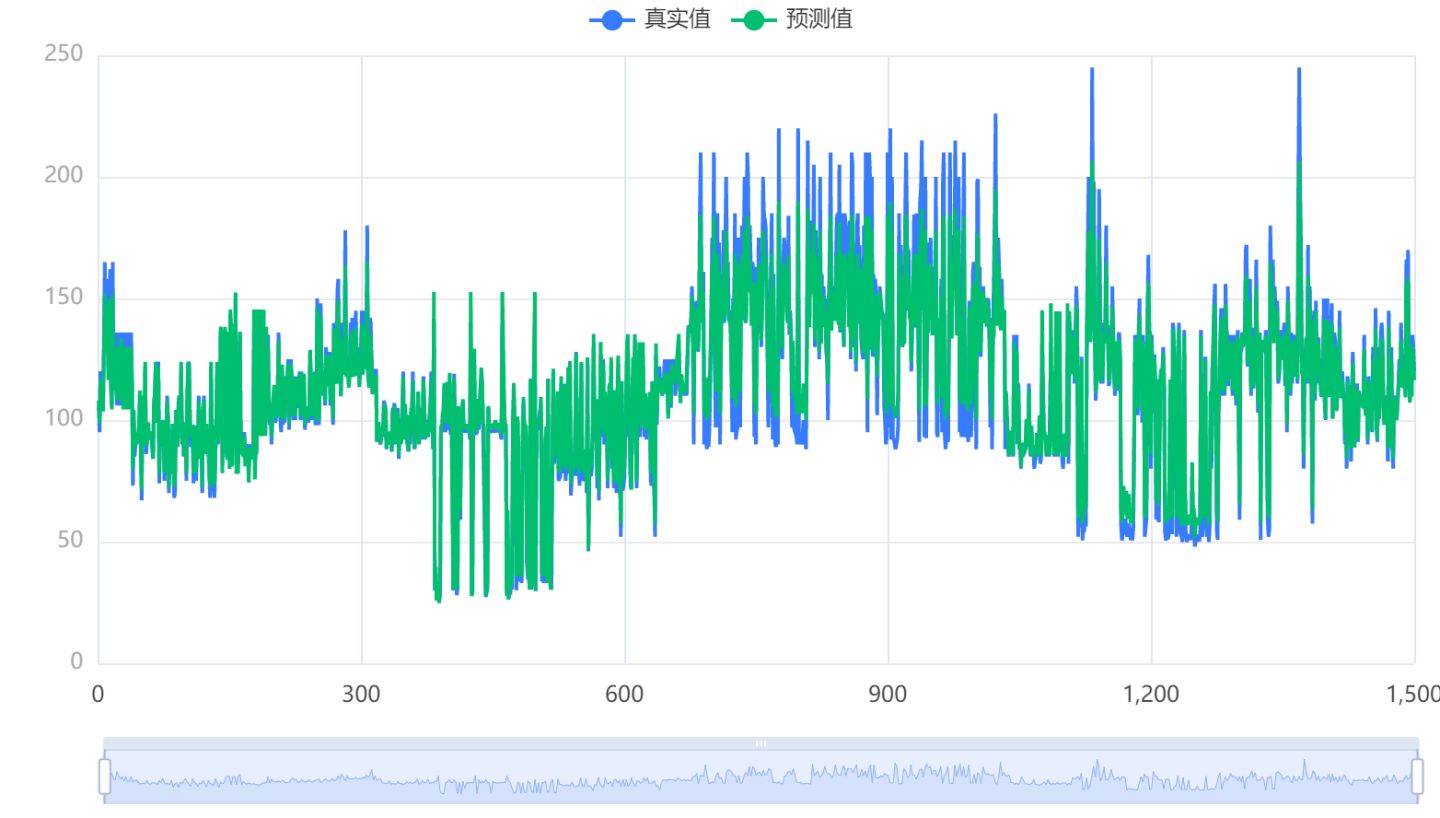
图表说明:上图以可视化的形式展示了本次模型的原始数据图、模型拟合值。
8、注意事项
- 一般在做岭回归之前,先采用线性回归(最小二乘法回归),如果发现自变量VIF(共线性)过大,如超过10,才使用岭回归;
- SPSSPRO采用方差扩大因子法来自动寻找K值;
- 选取 k值的一般原则是:
- 各回归系数的岭估计基本稳定
- 用最小二乘法估计的符号不合理的回归系数,其岭估计的符号变得合理
- 回归系数没有不合乎经济意义的绝对值
- 残差平方和增加不太多
9、模型理论
岭回归(Ridge Regression)是回归方法的一种,属于统计方法。在机器学习中也称作权重衰减。也有人称之为Tikhonov正则化。岭回归主要解决的问题是两种:一是当预测变量的数量超过观测变量的数量的时候(预测变量相当于特征,观测变量相当于标签),二是数据集之间具有多重共线性,即预测变量之间具有相关性。
一般的,回归分析的(矩阵)形式如下:
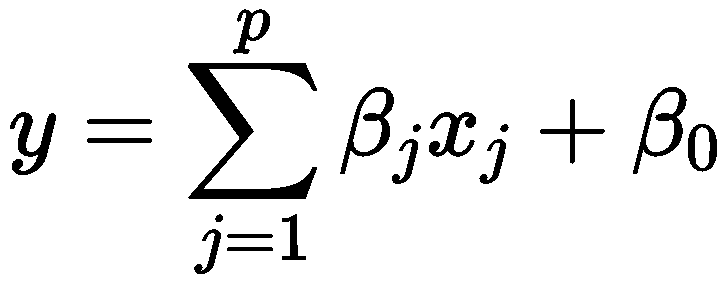
一般情况下,使用最小二乘法求解上述回归问题的目标是最小化如下的式子:
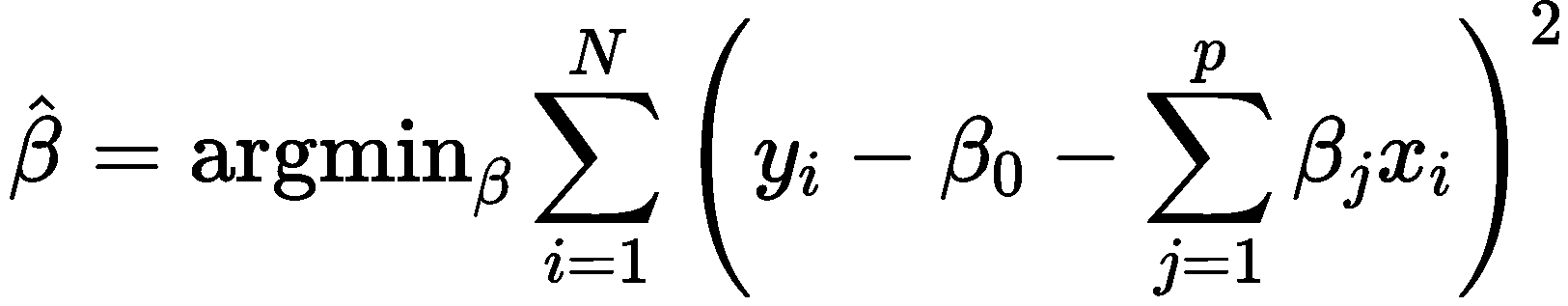
岭回归就是要在上述最小化目标中加上一个惩罚项:
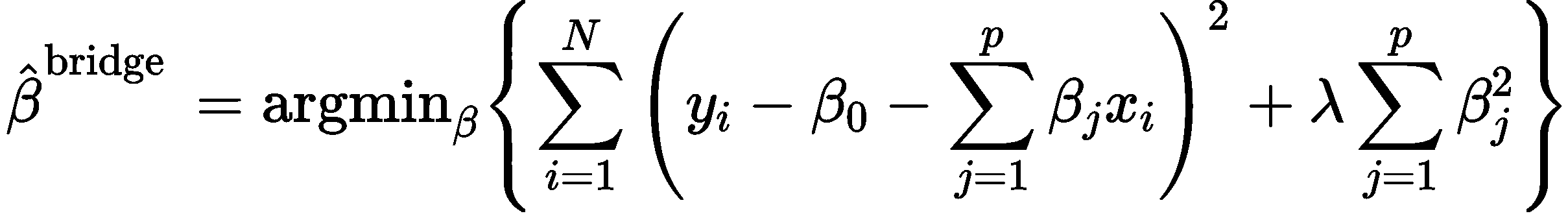
这里的λ也是待求参数。也就是说,岭回归是带二范数惩罚的最小二乘回归。
10、参考文献
[1] 刘超,回归分析——方法、数据与R的应用,高等教育出版社,2019