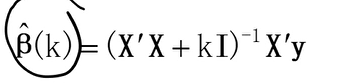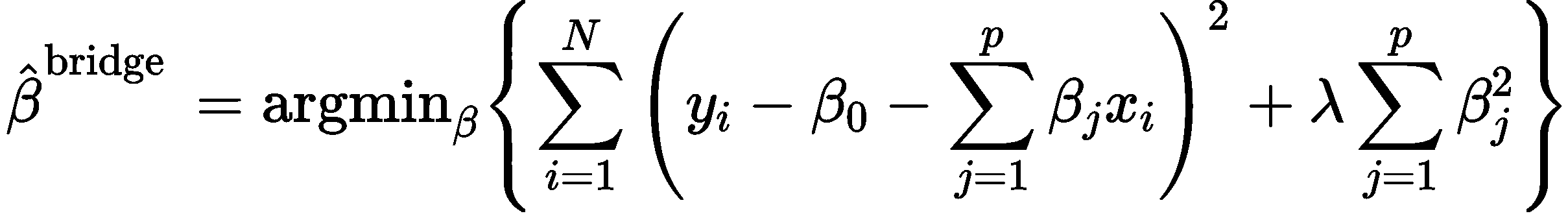1 岭回归的引入

在线性回归-正规方程和梯度下降中，我们介绍了基于正规方程或者梯度下降的优化算法，来寻找最优解。
在正规方程解中，它是基于直接求导得到最优解，公式如下：
在这里插入图片描述
但是，遇到如下情况的时候，正规方程无法求解。

数据中有多余的特征，例如数据中有两组特征是线性相关的，此时需要删除其中一组特征。
特征数大于样本数。如果数据的特征（X）比样本点（y）还多，即数据特征n，样本个数m，如果n>m，那么计算(𝑋𝑇𝑋)−1时会出错。因为(𝑋𝑇𝑋)不是满秩矩阵，所以不可逆。

矩阵可逆的条件可以参考学习：
（1）线性代数学习笔记——第二十讲——矩阵秩的定义
（2）矩阵不可逆的条件
（3）可逆矩阵的等价条件
在这里插入图片描述
所以，为了解决这个问题，统计学家引入了岭回归的概念（ridge regression）。下面介绍一下：

岭回归(英文名：ridge regression, Tikhonov regularization)：一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。

病态矩阵的意思是：矩阵中某个元素的一个很小的变动，会引起最后计算结果误差很大。

2 岭回归的原理

2.1 原理介绍

岭回归的原理学习自：
岭回归原理及代码实现

岭回归最早是用来处理特征数多于样本的情况，现在也用于在估计中加入偏差，从而得到更好的估计。同时也可以解决多重共线性的问题。岭回归是一种有偏估计。

它是相对于对于OLS（最小二乘法）这种无偏估计来说的。对于一个适定问题，X通常是列满秩的，那么我们可以采用最小二乘法，定义损失函数为残差的平方，最小化损失函数，求导求出最优解。
在这里插入图片描述

但是，正如开头所讲的问题，面临X不满足列满秩下或者某些列之间的线性相关性比较大时，XTX的行列式接近于0，即XTX接近于奇异，上述问题变为一个不适定问题，此时，计算【（XTX）-1】时误差会很大，传统的最小二乘法缺乏稳定性与可靠性。就像我开头讲的，不可逆了，正规方程不管用。
所以，为了解决上述问题，我们需要将不适定问题转化为适定问题：我们为上述损失函数加上一个正则化项（如降低某些特征的权重），变为
在这里插入图片描述
其中，我们定义

于是：

岭系数为在这里插入图片描述）
𝐼为单位矩阵(对角线上全为1，其他元素全为0)

整体而言，岭回归是对最小二乘回归的一种补充，它损失了无偏性，来换取高的数值稳定性，从而得到较高的计算精度。总结：

2.2 原理代码实现

"""
原理的代码实现
"""
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
import pandas as pd# 读入数据
data = genfromtxt(r"longley.csv", delimiter=',')
# print(pd.read_csv(r"longley.csv", delimiter=','))
# print(data)# 切分数据
x_data = data[1:, 2:]
# np.newaxis 变成二维
y_data = data[1:, 1, np.newaxis]
# print(x_data)
print(y_data)# print(np.mat(x_data).shape)  # 16个数据，6个特征
# print(np.mat(y_data).shape)  # 16个数据
# 给样本添加偏置项（常数b）
X_data = np.concatenate((np.ones((16, 1)), x_data), axis=1)
# print(X_data.shape)# 岭回归标准方程法求解回归参数
def weights(xArr, yArr, lam=0.2):  # 设置岭系数为0.2xMat = np.mat(xArr)yMat = np.mat(yArr)xTx = xMat.T * xMat  # 矩阵乘法  xMat.shape => (16,7)rxTx = xTx + np.eye(xMat.shape[1]) * lam  # 岭回归求解的括号的部分# 计算矩阵的值,如果值为0，说明该矩阵没有逆矩阵if np.linalg.det(rxTx) == 0.0:print("This matrix cannot do inverse")return# xTx.I为xTx的逆矩阵ws = rxTx.I * xMat.T * yMatreturn wsws = weights(X_data, y_data)
# print(ws)# 计算预测值
print(np.mat(X_data)*np.mat(ws))

3 API 实现

法1：

sklearn.linear_model.Ridge(alpha=1.0, fit_intercept=True,solver="auto", normalize=False)

具有I2正则化的线性回归
alpha:正则化力度，也叫 λ
λ取值：0~1 1~10
solver:会根据数据自动选择优化方法

sag:如果数据集、特征都比较大，选择该随机梯度下降优化)

normalize:数据是否进行标准化

normalize=False:可以在fit之前调用preprocessing.StandardScaler标准化数据

Ridge.coef_:回归权重
Ridge.intercept_:回归偏置
Ridge方法相当于SGDRegressor(penalty=‘l2’, loss=“squared_loss”),只不过SGDRegressor实现了一个普通的随机梯度下降学习，推荐使用Ridge(实现了SAG)

法2：
sklearn.linear_model.RidgeCV(_BaseRidgeCV, RegressorMixin)
具有l2正则化的线性回归，可以进行交叉验证
coef_:回归系数

class _BaseRidgeCV(LinearModel):def __init__(self, alphas=(0.1, 1.0, 10.0),fit_intercept=True, normalize=False,scoring=None,cv=None, gcv_mode=None,store_cv_values=False):

下面以波士顿房价为例

from sklearn.linear_model import Ridge
from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_errordef ridge_demo():# 1 数据加载data = load_boston()#2 数据集的划分x_train, x_test, y_train, y_test = train_test_split(data.data, data.target, random_state=22)#3 特征工程 - 标准化transfer = StandardScaler()x_train = transfer.fit_transform(x_train)x_test = transfer.fit_transform(x_test)#4 岭回归estimator = Ridge(alpha=1) # 法1# estimator = RidgeCV(alphas=(0.1, 1, 10))  # 法2estimator.fit(x_train, y_train)# 5 模型评估# 5.1 获取系数等值y_predict = estimator.predict(x_test)print("预测值为:\n", y_predict)print("模型中的系数为:\n", estimator.coef_)print("模型中的偏置为:\n", estimator.intercept_)# 5.2 评价# 均方误差error = mean_squared_error(y_test, y_predict)print("误差为:\n", error)if __name__ == '__main__':ridge_demo()