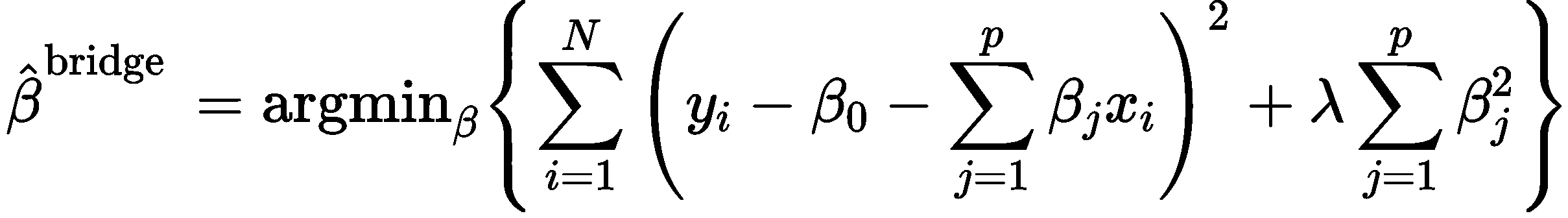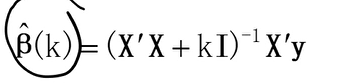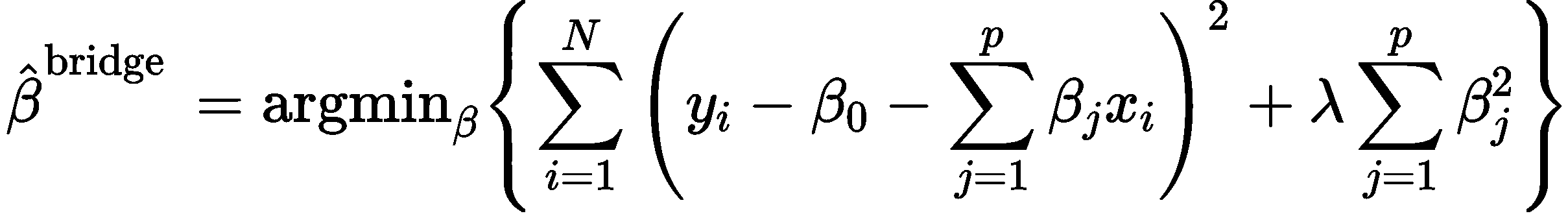多元线性回归-岭回归

1.精确相关关系

2.高度相关关系

3.多重共线性与相关性

4.岭回归

5.linear_model.Ridge

5.1.案例1：加利福尼亚房屋价值数据

5.2.案例2:波士顿房价数据集

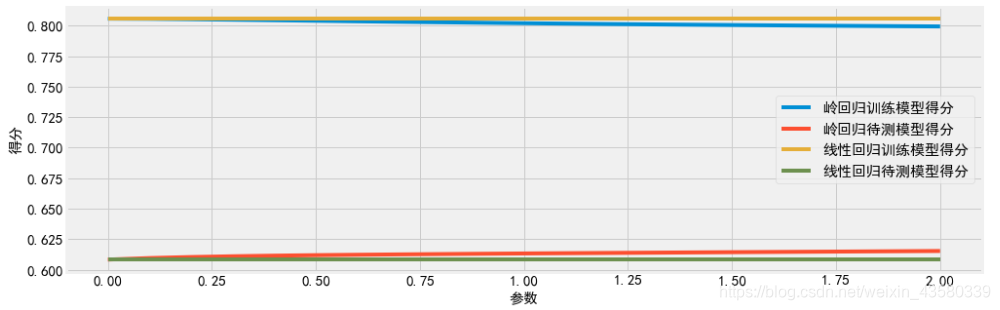
6.选取最佳正则化参数取值

1.精确相关关系

$A=\begin{bmatrix} 1 & 1& 2\\ 5 & 3& 11\\ 2& 2& 4 \end{bmatrix}=\begin{bmatrix} 1 & 1& 2\\ 0 & -2& 1\\ 0& 0& 0 \end{bmatrix}$

精确相关关系，即完全相关。如矩阵A并不是满秩矩阵，它有全零行，行列式等于0。A中存在着完全具有线性关系的两行（1,1,2）和（2,2,4），矩阵A中第一行和第三行的关系被称为“精确相关关系”，即完全相关。在这种精确关系下，矩阵A的行列式为0，则矩阵的逆矩阵不存在。在最小二乘法中，如果矩阵 $X^{T}X$ 存在这种精确相关关系，则逆矩阵不存在，最小二乘法无法使用，线性回归无法求出结果。

$X^{T}X=\frac{1}{\left | X^{T}X \right |}X^{T}X^{*}\rightarrow \frac{1}{0}X^{T}X^{*}\$

2.高度相关关系

$B=\begin{bmatrix} 1 & 1& 2\\ 5& 3& 11\\ 2& 2& 4.002 \end{bmatrix}=\begin{bmatrix} 1 & 1& 2\\ 0& -2& 1\\ 0& 0& 0.002 \end{bmatrix}$

矩阵B中第一行和第三行的关系不太一样，他们之间非常接近于“精确相关关系”，但又不是完全相关，一行接近0，另一行接近0，这种关系被称为“高度相关关系”。在这种高度相关关系下，矩阵的行列式不为0，矩阵的逆存在，不过接近无限大。在这种情况下，最小二乘法可以使用，但得到的逆会很大，直接影响对参数 $w$ 的求解：

$X^{T}X=\frac{1}{X^{T}X}X^{T}X^{*}\rightarrow \frac{1}{lim0}X^{T}X^{*}\rightarrow \infty$

$w=(X^{T}X)^{-1}X^{T}y\rightarrow \infty$

这样求解出来的参数向量 $w$ 会很大，会影响建模的结果，造成模型有偏差或模型不可用。精确相关关系和高度相关关系并称为“多重共线性”。在多重共线性下，模型无法建立或不可用。

3.多重共线性与相关性

多重共线性如果存在，则线性回归就无法使用最小二乘法进行求解，或者求解结果出现偏差。但不能存在多重共线性不代表不能存在相关性——机器学习不要求特征之间必须独立，必须不相关，只要不是高度相关或精确相关就好。

多重共线性Multicollinearity与相关性Correlation

多重共线性是一种统计现象，是指线性模型中的特征（解释变量）之间由于存在精确相关关系或高度相关关系，多重共线性的村子会使模型无法建立，或者估计失真。多重共线性使用指标方差膨胀因子（variance inflation factor,VIF）来进行衡量，通常当我们提到“共线性”，都特指多重共线性。

相关性是衡量两个或多个变量一起波动的程度的指标，它可以是正的，负的或者0，当我们说变量之间具有相关性，通常是指线性相关性，线性相关一般由皮尔逊相关系数进行衡量，非线性相关可以使用斯皮尔曼相关系数或者互信息法进行衡量。

4.岭回归

岭回归，又称为吉洪诺夫正则化（Tikhonov regularization）。岭回归在多元线性回归的损失函数上加上了正则项，表达为系数 $w$ 的L2范式（即系数 $w$ 的平方项）乘以正则化系数 $\alpha$ 。岭回归的损失函数的完整表达式写作：

$min\left| | Xw-y |\right |_{2}^{2}+\alpha \left| | w |\right |_{2}^{2}$

通过在损失函数上对 $w$ 求导来求解极值，最终得出：

$w=(X^{T}X+\alpha I)^{-1}X^{T}y$

如此，正则化系数 $\alpha$ 就避免了“精确相关关系”带来的影响，至少最小二乘法在 $\alpha$ 存在的情况下是一定可以使用了。对于存在“高度相关关系”的矩阵，我们也可以通过调大 $\alpha$ ，来让 $(X^{T}X+\alpha I)$ 矩阵的行列式变大，从而让逆矩阵变小，以此控制参数向量 $w$ 的偏移。当 $\alpha$ 越大，模型越不容易受到共线性的影响。当然， $\alpha$ 挤占了 $w$ 中由原始的特征矩阵贡献的空间，因此如果 $\alpha$ 太大，也会导致 $w$ 的估计出现较大的偏移，无法正确拟合数据的真实面貌。因此，我们在使用中，需要找出让模型效果变好的最佳 $\alpha$ 值。

5.linear_model.Ridge

在sklearn中，岭回归由线性模型库中的Ridge类来调用：

class sklearn.linear_model.Ridge(alpha=1.0,fit_intercept=True,normalize=False,copy_X=True,max_iter=None,tol=0.001,solver="auto",random_state=None)

和线性回归相比，岭回归的参数是多了一点，但真正核心的参数就是正则项的系数 $\alpha$ ，其他的参数是当我们希望用最小二乘法之外的求解方法求解岭回归的时候才需要，通常情况下是不会去触碰这些参数的。

5.1.案例1：加利福尼亚房屋价值数据

import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge,LinearRegression,Lasso
from sklearn.model_selection import train_test_split as TTS
from sklearn.datasets import fetch_california_housing as fch
import matplotlib.pyplot as plthousevalue=fch()
x=pd.DataFrame(housevalue.data)
y=housevalue.target
x.columns=["住户收入中位数","房屋使用年代中位数","平均房间数目","平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"]
xtrain,xtest,ytrain,ytest=TTS(x,y,test_size=0.3,random_state=420)
# 数据集索引恢复
for i in [xtrain,xtest]:i.index=range(i.shape[0])
# 使用岭回归来进行建模
reg=Ridge(alpha=1).fit(xtrain,ytrain)
reg.score(xtest,ytest)
# 交叉验证下，与线性回归相比，岭回归的结果如何变化
from sklearn.model_selection import cross_val_score
alpharange=np.arange(1,1001,100)
ridge,lr=[],[]
for alpha in alpharange:reg=Ridge(alpha=alpha)linear=LinearRegression()regs=cross_val_score(reg,x,y,cv=5,scoring="r2").mean()linears=cross_val_score(linear,x,y,cv=5,scoring="r2").mean()ridge.append(regs)lr.append(linears)
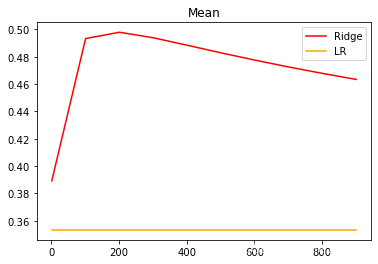
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()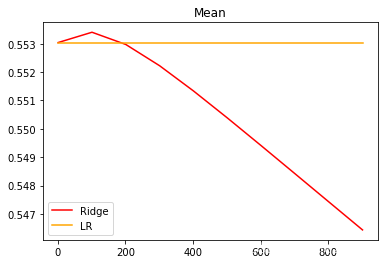

细化学习曲线：

alpharange=np.arange(1,201,10)
ridge,lr=[],[]
for alpha in alpharange:reg=Ridge(alpha=alpha)linear=LinearRegression()regs=cross_val_score(reg,x,y,cv=5,scoring="r2").mean()linears=cross_val_score(linear,x,y,cv=5,scoring="r2").mean()ridge.append(regs)lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()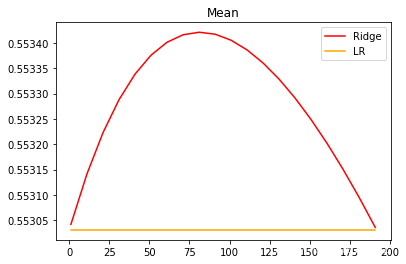

可以看出，激励福尼亚房屋价值数据集上，岭回归的结果轻微上升，随后骤降。可以说，加利福尼亚数据集上存在轻微的共线性，这种共线性被正则化参数 $\alpha$ 消除后，模型的效果提升了一点点，但是对于整个模型而言是杯水车薪。在过了控制多重性的点之后，模型的效果飞速下降，显然是正则化的程度太重，挤占了参数 $w$ 本来的估计空间。从整个结果可以看出，加利福尼亚数据和核心问题不在于多重共线性，岭回归不能够提升模型表现。

另外，在正则化参数不断增大的过程中，观察模型的方差如何变化：

alpharange=np.arange(1,1001,100)
ridge,lr=[],[]
for alpha in alpharange:reg=Ridge(alpha=alpha)linear=LinearRegression()var_regs=cross_val_score(reg,x,y,cv=5,scoring="r2").var()var_linears=cross_val_score(linear,x,y,cv=5,scoring="r2").var()ridge.append(var_regs)lr.append(var_linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Variance")
plt.legend()
plt.show()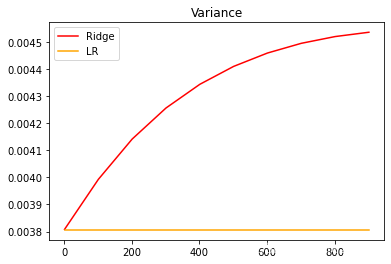

5.2.案例2:波士顿房价数据集

from sklearn.datasets import load_boston
x=load_boston().data
y=load_boston().target
xtrain,xtest,ytrain,ytest=TTS(x,y,test_size=0.3,random_state=420)
alpharange=np.arange(1,1001,100)
ridge,lr=[],[]
for alpha in alpharange:reg=Ridge(alpha=alpha)linear=LinearRegression()regs=cross_val_score(reg,x,y,cv=5,scoring="r2").mean()linears=cross_val_score(linear,x,y,cv=5,scoring="r2").mean()ridge.append(regs)lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()

细化学习曲线：

alpharange=np.arange(100,300,10)
ridge,lr=[],[]
for alpha in alpharange:reg=Ridge(alpha=alpha)linear=LinearRegression()regs=cross_val_score(reg,x,y,cv=5,scoring="r2").mean()linears=cross_val_score(linear,x,y,cv=5,scoring="r2").mean()ridge.append(regs)lr.append(linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
# plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Mean")
plt.legend()
plt.show()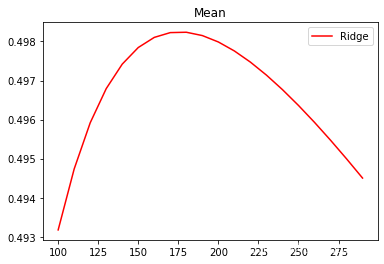

在正则化参数不断增大的过程中，观察模型的方差如何变化：

alpharange=np.arange(1,1001,100)
ridge,lr=[],[]
for alpha in alpharange:reg=Ridge(alpha=alpha)linear=LinearRegression()var_regs=cross_val_score(reg,x,y,cv=5,scoring="r2").var()var_linears=cross_val_score(linear,x,y,cv=5,scoring="r2").var()ridge.append(var_regs)lr.append(var_linears)
plt.plot(alpharange,ridge,color="red",label="Ridge")
plt.plot(alpharange,lr,color="orange",label="LR")
plt.title("Variance")
plt.legend()
plt.show()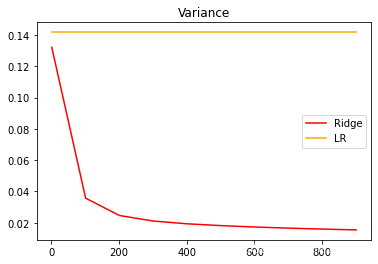

可以发现，比起加利福尼亚房屋价值数据集，波士顿房价数据集的方差降低明显，偏差也明显降低，可见使用岭回归还是起到了一定的作用，模型的泛化能力是有可能会上升的。

6.选取最佳正则化参数取值

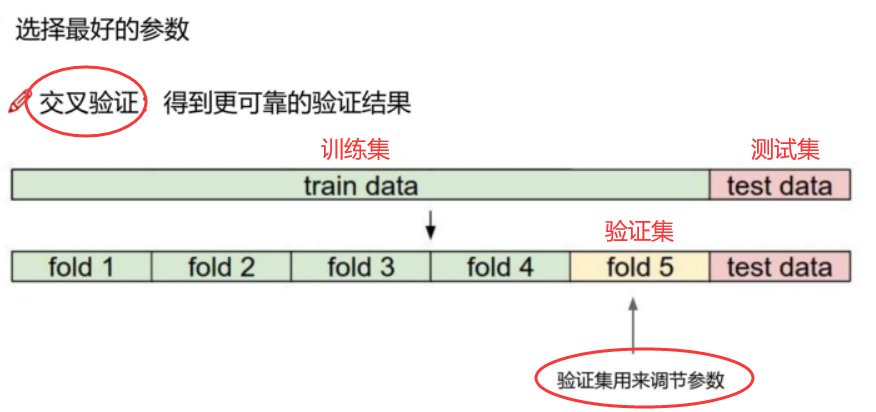
在sklearn中，使用带交叉验证的岭回归来选择最佳的正则化系数：

class sklearn.linear_model.RidgeCV(alphas=(0.1,1.0,10.0),fit_intercept=True,normalize=False,scoring=None,cv=Nonegcv_mode=None,store_cv_values=False)

可以看出，这个类与普通的岭回归非常相似，不过在输入正则化系数的时候可以传入元组作为正则化系数的备选，非常类似于在化学习曲线前设定的for i in的列表对象。

RidgeCV的重要参数：

重要参数	含义
alpha	需要测试的正则化参数的取值元组
scoring	用来进行交叉验证的模型评估指标，默认是 $R^{2}$ ，可自行调整
store_cv_values	是否保存每次交叉验证的结果，默认为False
cv	交叉验证的模式，默认是None，标傲世默认进行留一交叉验证可以输入Kfold对象和StratifiedKFold对象来进行交叉验证，注意，仅仅当store_cv_values=None时，每次交叉验证的结果才可以被保存下来。当cv有存在值时，store_cv_values无法被设定为True

RidgeCV的重要属性：

重要属性	含义
alpha_	查看交叉验证选中的alpha
cv_values_	调用所有交叉验证的结果，只有当store_cv_values=True时才能调用，因此返回的结构是（n_samples,n_alphas）

RidgeCV的重要接口：

重要接口	含义
score	调用Ridge类不进行交叉验证的情况下返回的R平方

housevalue=fch()
x=pd.DataFrame(housevalue.data)
y=housevalue.target
x.columns=["住户收入中位数","房屋使用年代中位数","平均房间数目","平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"]from sklearn.linear_model import RidgeCV
Ridge_=RidgeCV(alphas=np.arange(1,1001,100)
#               ,scoring="neg_mean_squared_error",store_cv_values=True
#               ,cv=5).fit(x,y)

Ridge_.score(x,y)

0.6060251767338444

# 进行平均后可以查看每个正则化系数取值下的交叉验证结果
Ridge_.cv_values_.mean(axis=0)

array([0.52823795, 0.52787439, 0.52807763, 0.52855759, 0.52917958,0.52987689, 0.53061486, 0.53137481, 0.53214638, 0.53292369])

# 查看被选择出来的最佳正则化系数
Ridge_.alpha_