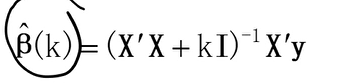python 岭回归算法之回归实操

基本概念

正则化

正则化是指对模型做显式约束，以避免过拟合。本文用到的岭回归就是L2正则化。（从数学的观点来看，岭回归惩罚了系数的L2范数或w的欧式长度）

正则化的具体原理就不在这里多叙述了，感兴趣的朋友可以看一下这篇文章：机器学习中正则化项L1和L2的直观理解。

算法简介

岭回归

岭回归也是一种用于回归的线性模型，因此它的模型公式与最小二乘法的相同，如下式所示：

y=w[0]*x[0]+w[1]*x[1]+w[2]x[2]+…+w[p]x[p]+b

但在岭回归中，对系数w的选择不仅要在训练数据上得到很好的预测结果，而且还要拟合附加约束。换句话说，w的所有元素都应接近于0。直观上来看，这意味着每个特征对输出的影响应尽可能小（即斜率很小），同时仍给出很好的预测结果，这个约束也就是正则化。

数据来源

波士顿房价：https://www.kaggle.com/altavish/boston-housing-dataset
~~也是非常经典的一个数据~~
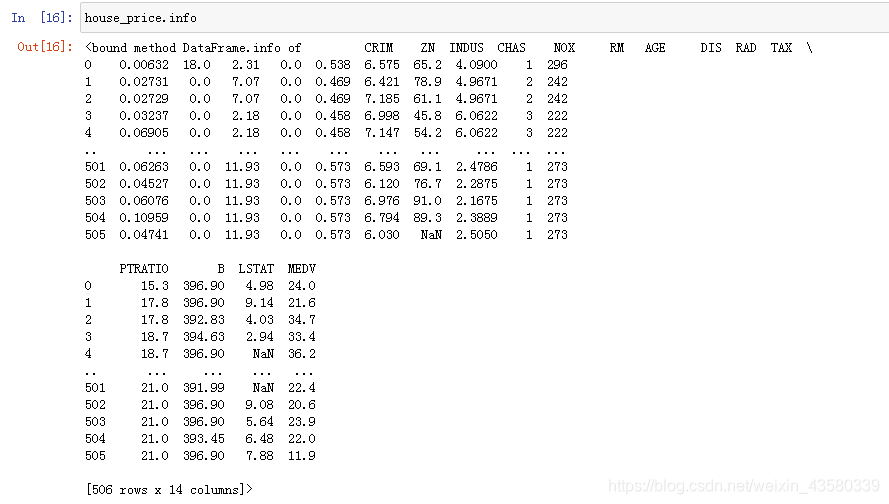
在这里插入图片描述

简单解释一下这个数据的几个主要指标：
ZN：25,000平方英尺以上的土地划为住宅用地的比例。
RM：每个住宅的平均房间数。
AGE：1940年之前建造的自有住房的比例
CHAS：有没有河流经过 (如果等于1，说明有，等于0就说明没有)
CRIM：犯罪率
MEDV：住房的价格
~~其它指标就不用说了，都是一些住房的其它指标，感兴趣的小伙伴可以自己查一下。~~

数据挖掘

1.导入第三方库

import pandas as pd
import numpy as np
import winreg
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge###导入岭回归算法
from sklearn.metrics import r2_score

老规矩，上来先依次导入建模需要的各个模块
2.读取文件

import winreg
real_address = winreg.OpenKey(winreg.HKEY_CURRENT_USER,r'Software\Microsoft\Windows\CurrentVersion\Explorer\Shell Folders',)
file_address=winreg.QueryValueEx(real_address, "Desktop")[0]
file_address+='\\'
file_origin=file_address+"\\源数据-分析\\HousingData.csv"#设立源数据文件的桌面绝对路径
house_price=pd.read_csv(file_origin)#https://www.kaggle.com/altavish/boston-housing-dataset

因为之前每次下载数据之后都要将文件转移到python根目录里面，或者到下载文件夹里面去读取，很麻烦。所以我通过winreg库，来设立绝对桌面路径，这样只要把数据下载到桌面上，或者粘到桌面上的特定文件夹里面去读取就好了，不会跟其它数据搞混。
~~其实到这一步都是在走流程，基本上每个数据挖掘都要来一遍，没什么好说的。~~

3.清洗数据
1.查找缺失值
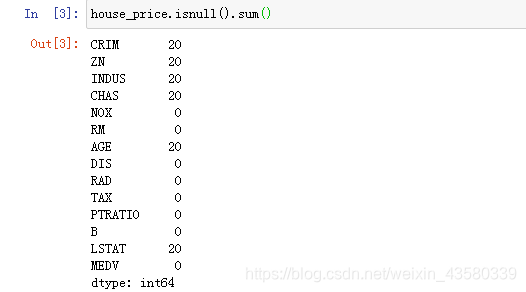
在这里插入图片描述

可以看到这个数据并包括一些缺失值，并不是很多，所以直接删掉就好了。

house_price1=house_price.dropna().reset_index()
del house_price1["index"]

2.突变值查找

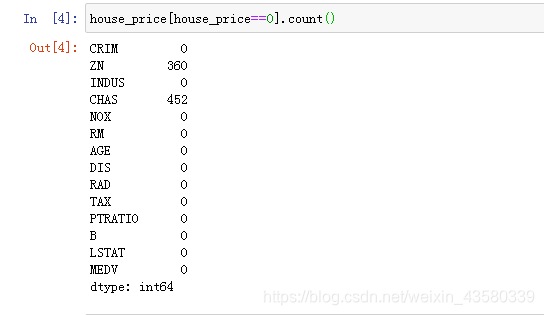
在这里插入图片描述
一般是看看特征值里面是否包含等于零的数据。其实说的直接一点就是看看数据里面是否包含不符合实际的数值，比如像是犯罪率，实际中不可能出现犯罪率等于0的片区。那么从上面的结果来看，这份数据并没有其它问题。
~~这份数据里面的ZN和CHAS都是利用0和1来当作一种指标，所以包含0是很正常的。~~
4.建模

train=house_price1.drop(["MEDV"],axis=1)
X_train,X_test,y_train,y_test=train_test_split(train,house_price1["MEDV"],random_state=1)
#将MEDV划分为预测值，其它的属性划分为特征值，并将数据划分成训练集和测试集。
ridge=Ridge(alpha=10)#确定约束参数
ridge.fit(X_train,y_train)
print("岭回归训练模型得分："+str(r2_score(y_train,ridge.predict(X_train))))#训练集
print("岭回归待测模型得分："+str(r2_score(y_test,ridge.predict(X_test))))#待测集

引入ridge算法，进行建模后，对测试集进行精度评分，得到的结果如下：
在这里插入图片描述

可以看到，该模型的训练精度为79%左右，对于新的数据来说，模型精度在63%左右。
至此，这个数据集的将建模就算是完成了。

讨论

1.参数的讨论

由于岭回归与线性回归（最小二乘法）的模型公式是一样的，所以这里我们与线性回归做一个比较。不了解线性回归的朋友可以看一下我的另一篇文章：最小二乘算法之回归实操
在这里插入图片描述

之前我们设立的约束参数是10，而上面模型参数设的是0，可以看出模型的训练精度有所提高，但泛化能力有所降低。同时与线性回归模型相比，二者的分数是完全一样的。所以，当岭回归的约束参数设为0时，失去约束的岭回归与普通最小二乘法就是同一个算法。

2.与普通最小二乘法的比较

我们通过变换约束参数的取值，来具体看一下岭回归与普通最小二乘法的优缺点。

result_b=pd.DataFrame(columns=["参数","岭回归训练模型得分","岭回归待测模型得分","线性回归训练模型得分","线性回归待测模型得分"])
train=house_price1.drop(["MEDV"],axis=1)
X_train,X_test,y_train,y_test=train_test_split(train,house_price1["MEDV"],random_state=23)
for i in range(21):alpha=i/10#约定参数可以选定为小数ridge=Ridge(alpha=alpha)ridge.fit(X_train,y_train)linear=LinearRegression()linear.fit(X_train,y_train)result_b=result_b.append([{"参数":alpha,"岭回归训练模型得分":r2_score(y_train,ridge.predict(X_train)),"岭回归待测模型得分":r2_score(y_test,ridge.predict(X_test)),"线性回归训练模型得分":r2_score(y_train,linear.predict(X_train)),"线性回归待测模型得分":r2_score(y_test,linear.predict(X_test))}])

结果如下所示：
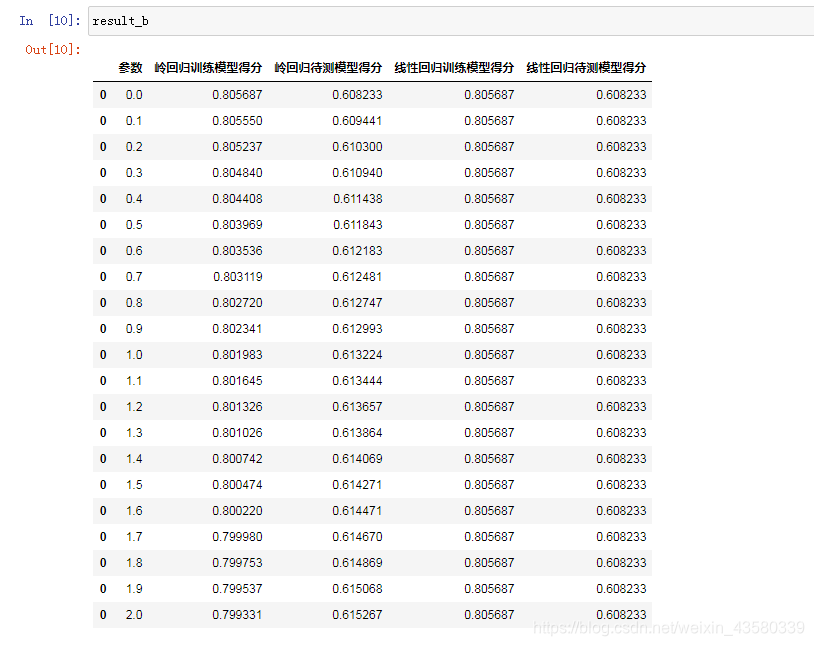
在这里插入图片描述
可以看出如果只是针对训练模型的精度，最小二乘法是要优于岭回归的，但是对新的数据作出预测时，也就是考虑模型的泛化能力上，可以看出岭回归的模型得分比最小二乘法要好一点。
我们通过一个折线图来更直观地表现上面的数据：

import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use("fivethirtyeight")
sns.set_style({'font.sans-serif':['SimHei','Arial']})#设定汉字字体，防止出现方框
%matplotlib inline
#在jupyter notebook上直接显示图表
fig= plt.subplots(figsize=(15,5))
plt.plot(result_b["参数"],result_b["岭回归训练模型得分"],label="岭回归训练模型得分")#画折线图
plt.plot(result_b["参数"],result_b["岭回归待测模型得分"],label="岭回归待测模型得分")
plt.plot(result_b["参数"],result_b["线性回归训练模型得分"],label="线性回归训练模型得分")
plt.plot(result_b["参数"],result_b["线性回归待测模型得分"],label="线性回归待测模型得分")
plt.rcParams.update({'font.size': 12})
plt.legend()
plt.xticks(fontsize=15)#设置坐标轴上的刻度字体大小
plt.yticks(fontsize=15)
plt.xlabel("参数",fontsize=15)#设置坐标轴上的标签内容和字体
plt.ylabel("得分",fontsize=15)

结果如下所示：
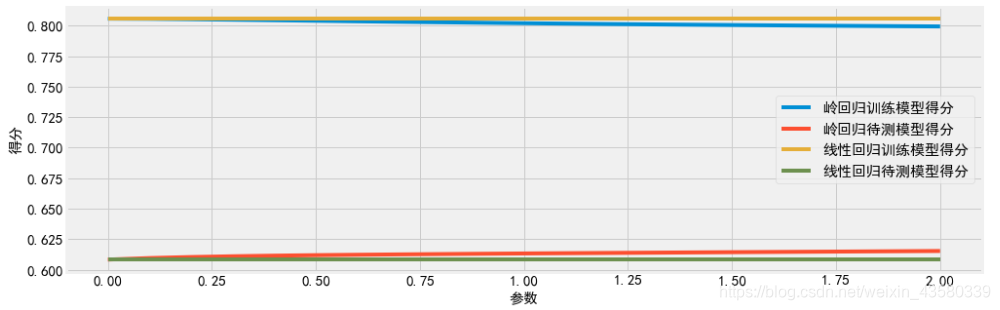
在这里插入图片描述
可以看出岭回归模型在模型的简单性（系数都接近于0）与训练集性能之间作出权衡。简单性和训练性能二者对于模型的重要程度可以由用户通过设置aplha参数来制定。增大alpha会使得系数更加趋向于0，从而降低训练集性能，但会提高泛化性能。

而且无论是岭回归还是线性回归，所有数据集大小对应的训练分数都要高于预测分数。由于岭回归是正则化的，所以它的训练分数要整体低于线性回归的训练分数。但岭回归的测试分数高，特别是对于较小的数据集。如果数据量小于一定程度的时候，线性回归将学不到任何内容，随着模型可用数据越来越多，两个模型的性能都在提升，最终线性回归的性能追上了岭回归。所以如果有足够多的训练内容，正则化变得不那么重要，并且岭回归和线性回归将具有相同的性能。

个人博客：https://www.yyb705.com/
欢迎大家来我的个人博客逛一逛，里面不仅有技术文，也有系列书籍的内化笔记。
有很多地方做的不是很好，欢迎网友来提出建议，也希望可以遇到些朋友来一起交流讨论。