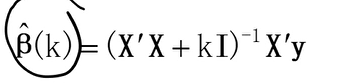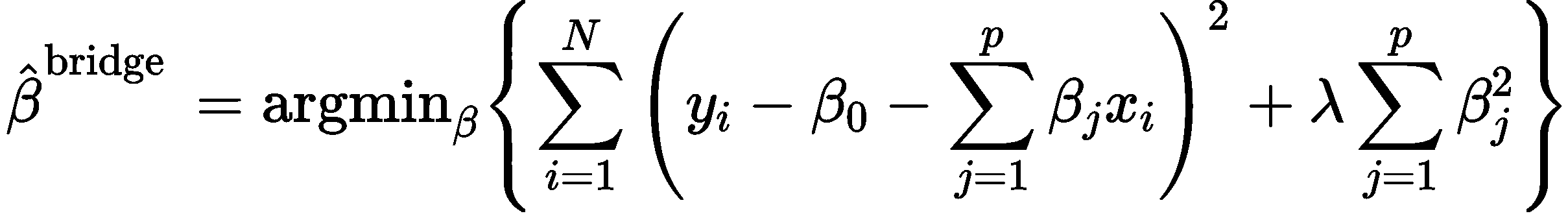线性回归
在多元线性回归模型中,估计回归系数使用的是OLS,并在最后讨论异方差和多重共线性对模型的影响。事实上,回归中自变量的选择大有门道,变量过多可能会导致多重共线性问题导致回归系数不显著,甚至造成OLS估计失效。
岭回归和lasso回归在OLS回归模型的损失函数上加上了不同的惩罚项,该惩罚项由回归系数的函数组成,一方面,加入的惩罚项能够识别出模型中不重要的变量,对模型起到简化作用,可以看作逐步回归法的升级版,另一方面,加入的惩罚项让模型变得可估计,即使原数据矩阵不满足列满秩。
线性回归模型
在标准线性回归中,通过最小化真实值( y i y_{i} yi)和预测值( y ^ i \hat{y}_{i} y^i)的平方误差来训练模型,这个平方误差值也被称为残差平方和(RSS, Residual Sum Of Squares):
R S S = ∑ i = 1 n ( y i − y ^ i ) 2 R S S=\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2} RSS=i=1∑n(yi−y^i)2
最小二乘法即最小残差平方和,为:
J β ( β ) = arg min β ∑ i = 1 p ( y i − x i β i − β 0 ) 2 J_{\beta}(\beta)=\underset{\beta}{\arg \min } \sum_{i=1}^{p}\left(y_{i}-x_{i} \beta_{i}-\beta_{0}\right)^{2} Jβ(β)=βargmini=1∑p(yi−xiβi−β0)2
将其化为矩阵形式:
J β ( β ) = arg min β ( Y − X β ) T ( Y − X β ) J_{\beta}(\beta)=\underset{\beta}{\arg \min }(Y-X \beta)^{T}(Y-X \beta) Jβ(β)=βargmin(Y−Xβ)T(Y−Xβ)
求解为:
β = ( X T X ) − 1 X T Y \beta=\left(X^{T} X\right)^{-1} X^{T} Y β=(XTX)−1XTY
由于求解 β \beta β,需要假设矩阵 X T X X^{T} X XTX是满秩矩阵
然而 X T X X^{T} X XTX往往不是满秩矩阵或者某些列之间的线性相关性比较大,例如会出现变量数(属性数)远超过样例数,导致 X X X的列数多于行数, X T X X^{T} X XTX显然不满秩,可解出多个 β \beta β,使得均方误差最小化,即在多元回归中,特征之间会出现多重共线问题,使用最小二乘法估计系数会出现系数不稳定问题,缺乏稳定性和可靠性。
岭回归
在矩阵 X T X X^{T} X XTX的对角线元素加一个小的常数值 λ \lambda λ,取其逆求得系数:
β ^ ridge = ( X T X + λ I n ) − 1 X T Y \hat{\beta}_{\text {ridge }}=\left(X^{T} X+\lambda I_{n}\right)^{-1} X^{T} Y β^ridge =(XTX+λIn)−1XTY
I n I_{n} In为单位矩阵,对角线全为1,类似山岭
λ \lambda λ是岭系数,改变其数值可以改变单位矩阵对角线的值
随后代价函数 J β ( β ) J_{\beta}(\beta) Jβ(β)在 R S S RSS RSS基础上加入对系数值的惩罚项:
J β ( β ) = R S S + λ ∑ j = 0 n β j 2 = R S S + λ ∥ β ∥ 2 \begin{aligned} J_{\beta}(\beta) &=R S S+\lambda \sum_{j=0}^{n} \beta_{j}^{2} \\ &=R S S+\lambda\|\beta\|^{2} \end{aligned} Jβ(β)=RSS+λj=0∑nβj2=RSS+λ∥β∥2
矩阵形式为:
J β ( β ) = ∑ i = 1 p ( y i − X i β ) 2 + λ ∑ j = 0 n β j 2 = ∑ i = 1 p ( y i − X i β ) + λ ∥ β ∥ 2 \begin{aligned} J_{\beta}(\beta) &=\sum_{i=1}^{p}\left(y_{i}-X_{i} \beta\right)^{2}+\lambda \sum_{j=0}^{n} \beta_{j}^{2} \\ &=\sum_{i=1}^{p}\left(y_{i}-X_{i} \beta\right)+\lambda\|\beta\|^{2} \end{aligned} Jβ(β)=i=1∑p(yi−Xiβ)2+λj=0∑nβj2=i=1∑p(yi−Xiβ)+λ∥β∥2
λ \lambda λ是超参数,用来控制对 β J \beta_{J} βJ的惩罚强度, λ \lambda λ值越大,生成的模型就越简单
λ \lambda λ的选择方法
1.岭迹分析法(主观性强)
(1)各回归系数的岭估计稳定
(2)用最小二乘法估计时符号不合理的回归系数,其岭估计的符号变得合理
(3)回归系数没有不合乎经济意义的绝对值
(4)残差平方和增长不太多
2.VIF法(方差膨胀因子)
若 β \beta β的 V I F VIF VIF>10,数据列与列指标之间存在多重共线性,因此我们可以不断增加 λ \lambda λ的值来不断减少 V I F VIF VIF,知道所有的 β \beta β的 V I F VIF VIF>10,确定理想的 λ \lambda λ的值
3.最小化均方预测误差(最广泛,最准确)
我们使用K折交叉验证的方法,来选择最佳的调整参数。所谓的k折交叉验证,就是把样本数据随机分为k等份,将第1个子样本作为验证集而保留不用,剩余k-1个子样本作为训练集来估计模型,再以此预测第1个子样本,并计算第1个子样本的均方预测误差(MSPE)。之后,将第2个子样本作为验证集,剩余k-1个子样本作为训练集来预测第2个子样本,并计算第二个子样本的MSPE。以此类推,将所有子样本的MSPE加总,可以获得整个样本的MSPE,最后选择调整参数,使得整个样本的MSPE最小,从而确定最理想的 λ \lambda λ的值,具有最佳的预测能力。
需要保证数据的量纲一致,若量纲不一致应对数据进行标准化处理。
Lasso回归
代价函数 J β ( β ) J_{\beta}(\beta) Jβ(β)在 R S S RSS RSS基础上加入对系数值的惩罚项:
J β ( β ) = R S S + λ ∑ j = 0 n ∣ β j ∣ = R S S + λ ∣ β ∣ \begin{aligned} J_{\beta}(\beta) &=R S S+\lambda \sum_{j=0}^{n} |\beta_{j}| \\ &=R S S+\lambda|\beta| \end{aligned} Jβ(β)=RSS+λj=0∑n∣βj∣=RSS+λ∣β∣
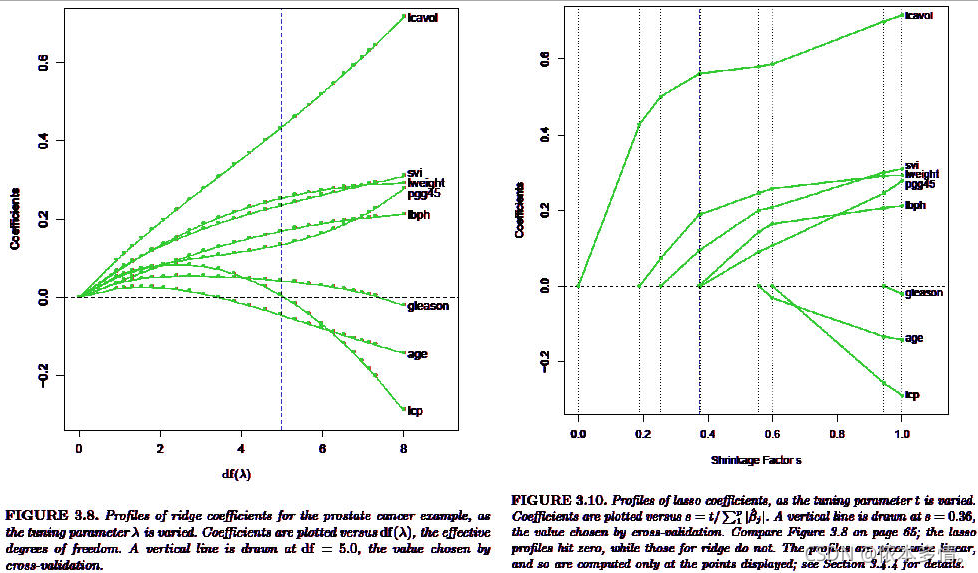
岭回归与Lasso回归最大的区别在于岭回归引入的是L2范数惩罚项,Lasso回归引入的是L1范数惩罚项。
矩阵形式为:
J β ( β ) = ∑ i = 1 p ( y i − X i β ) 2 + λ ∑ j = 0 n ∣ β j ∣ = ∑ i = 1 p ( y i − X i β ) + λ ∣ β ∣ \begin{aligned} J_{\beta}(\beta) &=\sum_{i=1}^{p}\left(y_{i}-X_{i} \beta\right)^{2}+\lambda \sum_{j=0}^{n} |\beta_{j}| \\ &=\sum_{i=1}^{p}\left(y_{i}-X_{i} \beta\right)+\lambda|\beta| \end{aligned} Jβ(β)=i=1∑p(yi−Xiβ)2+λj=0∑n∣βj∣=i=1∑p(yi−Xiβ)+λ∣β∣
其中 λ \lambda λ称为正则化参数,如果 λ \lambda λ选取过大,会把所有参数θ均最小化,造成欠拟合,如果 λ \lambda λ选取过小,会导致对过拟合问题解决不当。
岭回归与Lasso回归最大的区别在于岭回归引入的是L2范数惩罚项,Lasso回归引入的是L1范数惩罚项。Lasso回归能够使得损失函数中的许多 β \beta β均变成0,这点要优于岭回归,因为岭回归是要所有的 β \beta β均存在的,这样计算量Lasso回归将远远小于岭回归。(升级版的逐步回归)
Lasso的缺点也很明显,Lasso没有显示解,只能使用近似估计算法(坐标轴下降法和最小角回归法)
案例分析
分析棉花年产量与种子费,化肥费,农药费,机械费,灌溉费之间的关系
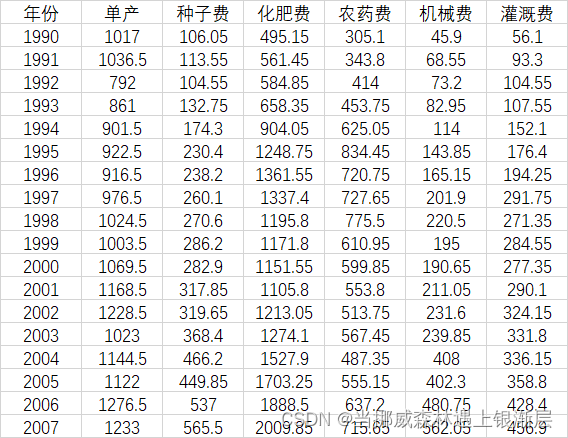
因为数据量纲一致,所以不需要对数据进行标准化处理,我们可以使用stata来对数据进行回归处理,在回归处理结束后,计算 β \beta β的方差膨胀因子检验变量之间是否存在多重共线性
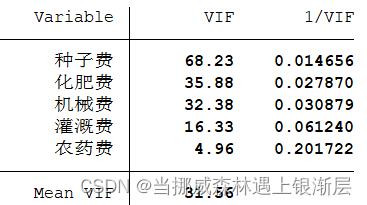
我们可以明显看到回归系数的 V I F VIF VIF明显大于10,因此变量之间有较强的多重共线性。
由于lasso回归的计算量显著小于岭回归,因此我们在处理多重共线性回归分析中大多使用lasso回归,在选择 λ \lambda λ时,岭迹分析法具有较强的主观性,不利于准确的测定,而 V I F VIF VIF法在实际中几乎不用,因为岭回归基本筛选不出变量,所以在实际生活大多使用最小化均方预测误差方法。

通过对数据进行最小化均方预测误差,stata会在最小的MSPE的一栏中标注*号,以此确定合适的 λ \lambda λ的值。
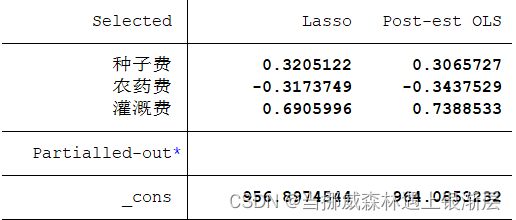
上表右边第1列即为Lasso所估计的变量系数。其中,除常数项外,只有3个变量的系数为非零,而其余变量(未出现在表中)的系数则为 0。考虑到作为收缩估计量的Lasso存在偏差(bias),上表右边第2列汇报了“Post Lasso”估计量的结果,即仅使用Lasso进行变量筛选,然后扔掉 Lasso 的回归系数,再对筛选出来的变量进行OLS回归。
注意:以上结果可能随着我们之前设置的随机数种子变化,因为lasso回归的估计是近似算法,且剔除的多重共线性变量是相对的。
总结
岭回归在stata使用中会存在bug,如遇到需要岭回归计算的问题,最好使用python实现
何时使用lasso回归:
我们首先使用一般的OLS对数据进行回归,然后计算方差膨胀因子 V I F VIF VIF,如果 V I F VIF VIF>10时,变量之间存在多重共线性,此时我们需要对变量进行筛选。
我们可以使用逐步回归法来筛选自变量,让回归中仅留下显著的自变量来抵消多重共线性的影响,在学习lasso后可以把lasso回归视为逐步回归法的进阶版,我们可以使用lasso回归来帮我们筛选出不重要的变量,步骤如下:
(1)判断自变量的量纲是否一样,如果不一样则首先进行标准化的预处理;(2)对变量使用lasso回归,记录下lasso回归结果表中回归系数不为0的变量,这些变量就是最终我们要留下来的重要变量,其余未出现在表中的变量可视为引起多重共线性的不重要变量。
在得到了重要变量后,我们实际上就完成了变量筛选,此时我们只将这些重要变量视为自变量,然后进行回归,并分析回归结果即可。(注意:此时的变量可以是标准化前的,也可以是标准化后的,因为lasso只起到变量筛选的目的)
岭回归python代码
def reg_model_Ridge(x,y,alphas,dim):''';岭回归估计:param x::param y::param alphas: 随机生成多个模型参数Lambda:param dim:维度:return: ridge_B 最优模型的系数'''model_coff=[]for alpha in alphas:ridge = Ridge(alpha=alpha,normalize=True)ridge.fit(x,y)model_coff.append(ridge.coef_)# if dim<=10:#plot_data(alphas, model_coff, 'Log Alpha', 'Cofficients', 'alpha系数与岭回归系数的关系 ,dim='+str(dim))# 交叉验证,找到模型最优的Lambda值ridge_cv= RidgeCV(alphas=alphas,normalize=True,scoring="neg_mean_absolute_error", cv=5)ridge_cv.fit(x,y)ridge_best_lambda = ridge_cv.alpha_# 建立最优模型ridge = Ridge(alpha=ridge_best_lambda,normalize=True)ridge.fit(x,y)# 得到最优模型的系数ridge_B = ridge.coef_return ridge_B