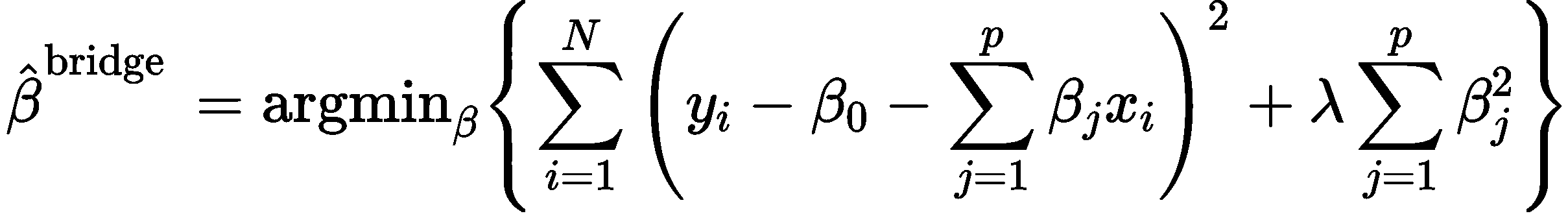岭回归存在的目的：

解决多重共线性下，最小二乘估计失效的问题

 

岭回归的作用：(在引入变量太多，又存在多重共线性，难以抉择去留哪个变量时可以通过该方法筛选变量)

1.找出多重共线性的变量，并提剔除部分

2.找出作用不大的变量

3.找出岭回归系数不稳定的变量

---

一、岭回归的定义和性质

1.背景：

在多元线性回归中得到变量的最小二乘估计

因此要保证的估计有效，就要求存在，即要求存在，从而要求矩阵X是满秩的，即非共线的。

当然X共线情况是很少几率会出现的，但是各个变量之间存在一定程度的线性相关是常常存在的，这会导致

，，

2.做法：

给参数的估计加一个修正，，为常数矩阵，取值为1，大小通过来调整

3.岭回归的性质;

1）是回归参数的有偏估计，因为加入了.

2）是的一个线性变换

                            

                             

但是通常k跟y是又直接关系的，并非独立开来，所以c在形式上上从本质上说并非的线性映射.

3），因为，

---

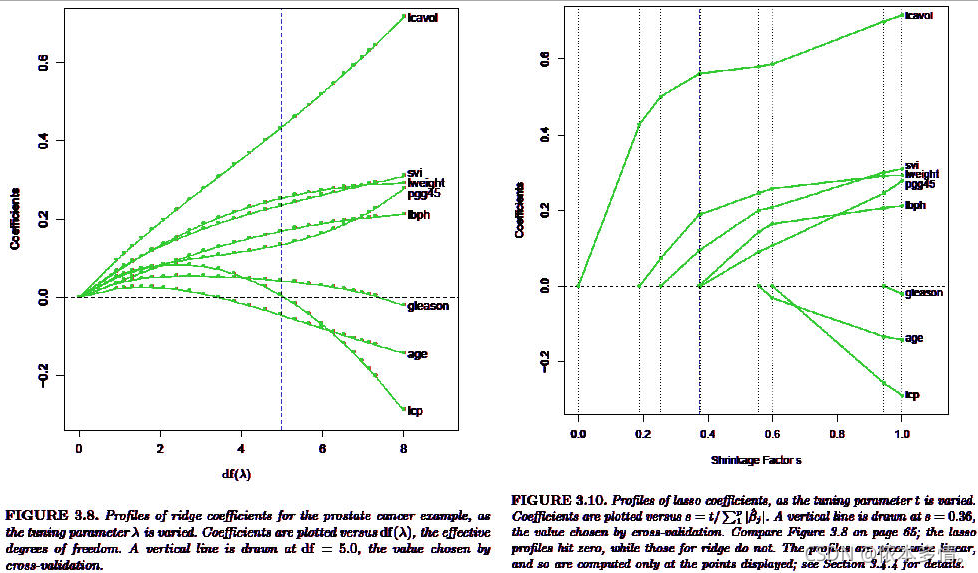
二、岭迹分析

a)可以看出k取0的时候,从古典的分析观点看，该变量具有重要的影响，但随着k的增加，迅速下降到负值，后趋近于0，基本上可以判定，该变量没有多大作用，可以去掉.

b)可以看出k取0的时候,但是绝对值不高，从古典的分析方法看，该变量没有太大作用，但随着k的增加迅速下降到负值，后趋于稳定，从岭回归的角度看该变量具有负影响。

c)可以看出k取0的时候,且绝对值较高高，从古典的分析方法看，该变量有较大的正影响，但随着k的增加迅速下降到负值，后趋于稳定，从岭回归的角度看该变量具有负影响。

d)都不稳定，但随着k的变化，其和大体上稳定，从岭回归的角度考虑该两变量存在共线性，保留一个就行，同时可以查看两个变量的相关系数。

e)各个变量的岭迹很混乱，变动较大，不适合用最小二乘估计.

f)各个变量的岭迹较稳定，可以放心使用最小二乘估计.

如果要选择岭回归代替最小二乘，k值的选取有三个参考标准.

1)岭迹法，看在哪个地方趋于稳定.

2)残差平方和，控制残差平方和变差都某个程度内选择k

3)方差扩大因子法.