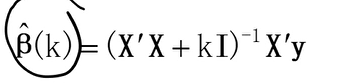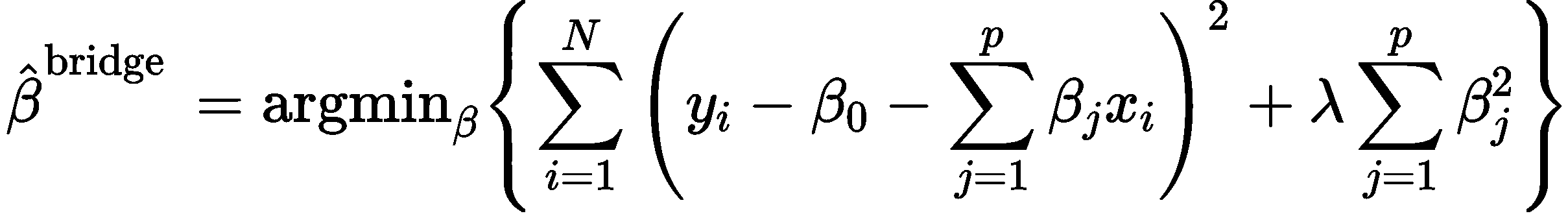岭参数的一般选择原则

• 选择k（或lambda）值，使得：
• 各回归系数的岭估计基本稳定
• 用最小二乘估计时符号不合理的回归系数，其岭回归的符号变得合理
• 回归系数没有不合乎实际意义的绝对值
• 残差平方和增大的不多

用R语言进行岭回归

这里使用MASS包中的longley数据集，进行岭回归分析（longley数据集中的变量具有显著的多重共线性）。从而分析使用岭回归进行多重共线性的解决。

首相将longley数据集中的第一列数据命名为“y”，并使用岭回归创建线性模型：

显示当y为因变量，其余各个变量为自变量时，直接构建线性模型的统计结果如下：

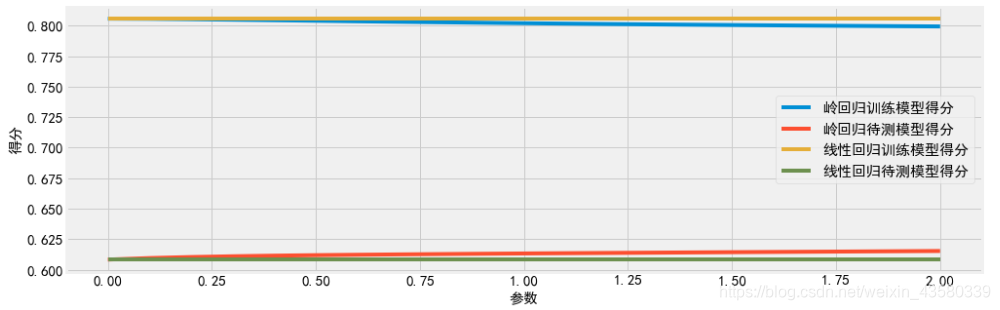
可见，虽然线性回归的Multiple R-squared： 0.9926是一个很高的值。但各个变量的显著性检验却很差，同样说明直接使用线性模型的拟合效果并不是很理想。

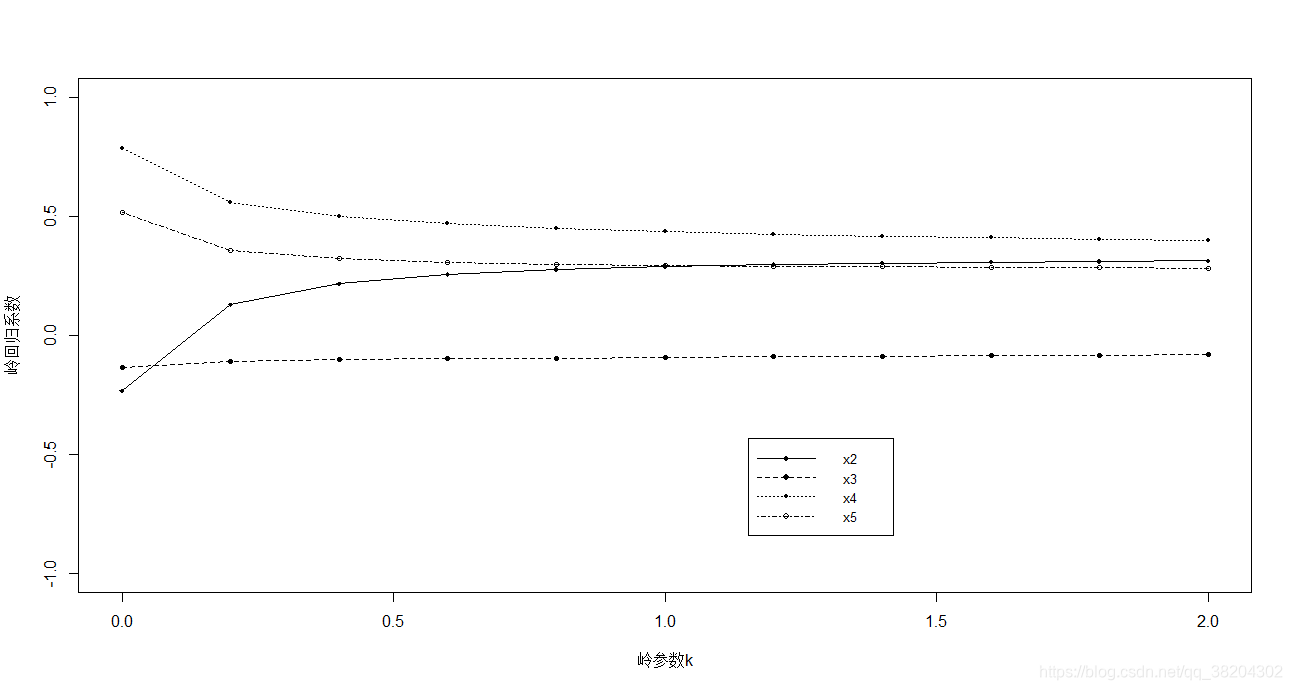
制定岭参数lamdba从0-0.1，每次变化的长度为0.001，并绘制岭迹图，如下：

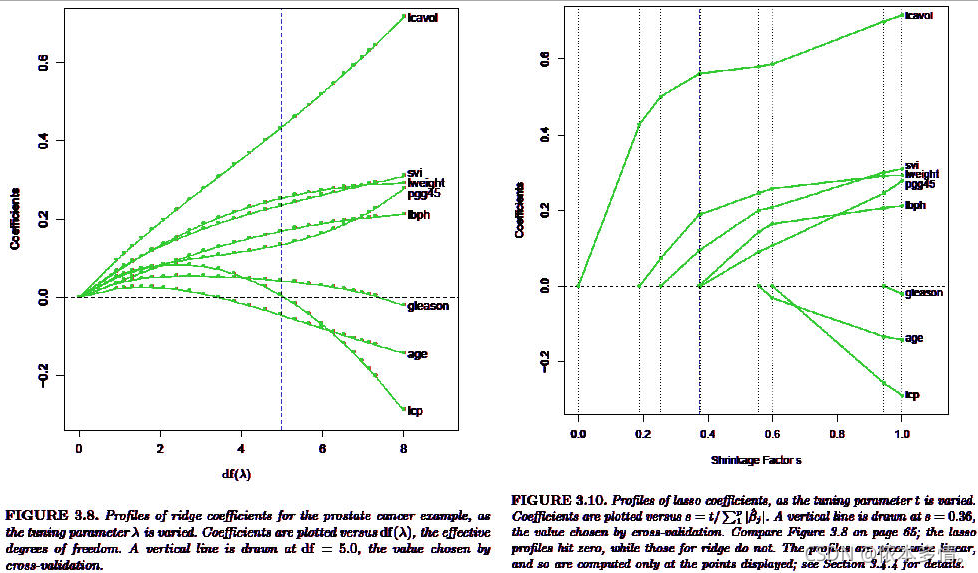
详细岭回归的岭迹图如下：

从岭迹图中可以看出，当lambda=0时，图像不稳定。因此，可以说明这里的变量存在多重共线性。

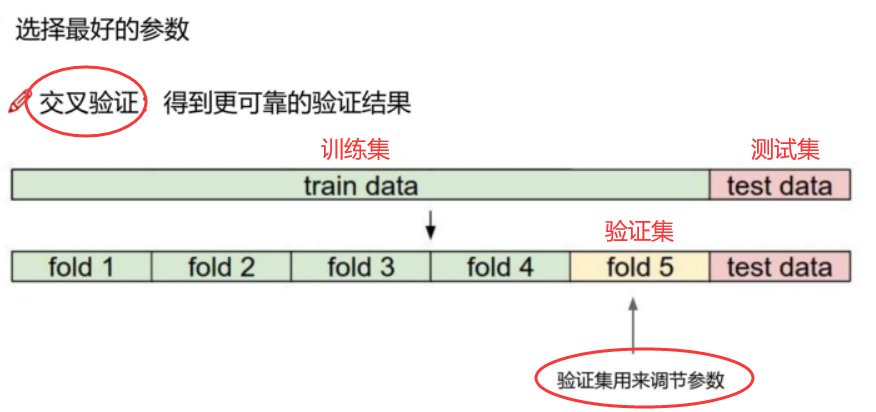
现在需要对岭参数lambda进行选择：

可以看出，这里由于使用了不同的估计方法，从而可以得到几个不同的岭参数的估计。通常取GCV估计，或者结合几个结果进行取值。这里取lambda=0.006。

使用R的ridge包的时候，出现如下问题：

岭回归的问题

• 岭参数计算方法太多，差异太大
• 根据岭迹图进行变量筛选，随意性太大
• 岭回归返回的模型（如果没哟经过变量筛选）包含所有的变量
• 而且，对于使用岭回归进行变量的筛选，目前只能作为一个扩展计算视野的方法，而在实际使用中，会出现很多问题。