数据结构与算法之树

数据结构与算法之树（一）二叉树概念及遍历方式（图文并茂）

数据结构与算法之树（二）二叉查找树

数据结构与算法之树（三）AVL树

数据结构与算法之树（四）红黑树

数据结构与算法之树（三）AVL树

一、什么是平衡二叉树？

上一篇文章在讲述二叉查找树的时候，在极端情况下二叉查找树的左右子树极不平衡，造成了搜索速率的低落，于是为了防止左右子树极不平衡的情况，有了平衡二叉查找树

所谓的“平衡”，没有一个绝对的测量标准，大致的意思是左右子树的高度差不多

不同的平衡条件，造就了不同的搜索、插入、删除的效率，以及不同的实现复杂度，常见的平衡二叉树有AVL树、红黑树等，本文将讲解AVL树

二、什么是AVL树？

AVL树规定，任何一个节点，左右子树的高度相差不大于1

如下图所示

左边的二叉树满足AVL树的要求，在插入值为2节点后，它不满足AVL树的要求了，因为值为4和5的节点它们的左右子树高度相差大于1

那么我们可以使用什么策略来进行调整，使其满足AVL树的要求呢？

三、AVL树的调整策略

将不平衡的二叉搜索树调整成AVL树，需要对指定节点进行旋转操作，下面先来讲以下旋转操作

3.1 旋转操作

旋转操作分为左旋和右旋

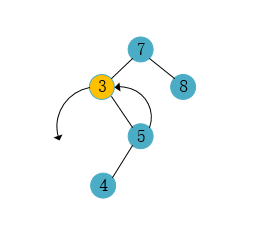
3.1.1 左旋

如上图所示，就是将3节点进行左旋操作

上图的操作中，是要进行左旋操作的节点它的右子节点没有左节点，也就是5节点没有左节点，设想一下如果5节点有左节点，那么对3节点进行左旋操作，会发生什么？

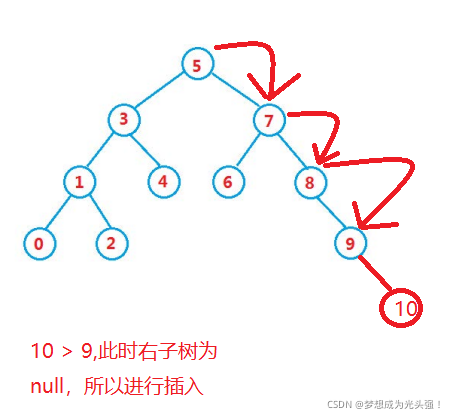
先想一下对下面这棵树的3节点进行左旋操作，会发生什么？

没错，会发生冲突，5节点会有两个左节点，这是二叉树不允许的，如下图所示

那么怎么解决冲突？

解决冲突的方法就是将冲突节点插入到指定位置，如上图，我们冲突的节点是4节点，而4节点是5节点的左子节点，肯定比5节点小，那么在进行旋转之后，将4节点按二叉查找树的插入规则插入到5节点的左子树即可，如下

适当小结一下

左旋操作会有两种情况

1.要左旋节点的右子节点没有左子节点，这种情况下不会发生冲突

2.要左旋节点的右子节点有左子节点，这种情况会发生冲突，解决冲突的方法就是将冲突节点插入到旋转后主节点的左子树

3.1.2 右旋

上图是对8节点进行右旋操作

如果5节点有右子节点，也会发生冲突，解决办法是将冲突节点插入到右子树中，如下所示

小结

右旋操作也有两种情况

1.进行右旋操作的节点的左子节点没有右子节点，这种情况不会发生冲突

2.进行右旋操作的节点的左子节点有右子节点，这种情况会发生冲突，解决冲突的办法是将冲突的节点插入到旋转后主节点的右子树

在理解左旋和右旋操作后，下面将将讲解AVL的调整策略

3.2 需要调整的节点

首先我们讨论在插入一个节点，使得二叉树不在是AVL树的时候，我们需要对哪个节点作出调整？

首先我们来看一个例子

上述这个例子，在插入2节点后，二叉树不在是AVL树，此时是因为4节点和5节点不满足AVL树的规定

这里我们要解决4节点，只要将4节点进行一次右旋操作，就可以解决问题，如下

我们可以得到一个规律是

需要调整的节点是不满足AVL树规定的节点中最深的那么节点（如4节点）

在清楚需要调整的节点后，我们来讲一讲需要调整的情况

3.3 情况分类

调整的情况可以分为4中

LL：插入节点在需要调整节点左子树的左子节点

LR：插入节点在需要调整节点左子树的右子节点

RR：插入节点在需要调整节点右子树的右子节点

RL：插入节点在需要调整节点右子树的左子节点

这四种情况都有各自的调整策略，下面将一一介绍

3.3.1 LL

对于这种情况，我们只需要将我们要调整的节点（4节点）进行一次右旋操作即可，如下

3.3.2 LR

对于这种情况，我们需要将调整节点（4节点）的左子节点（2节点）进行一个左旋，然后再对调整节点（4节点）进行一次右旋，如下

3.3.3 RR

对于这种情况我们只需要将调整节点（4节点）进行一次左旋即可，如下

3.3.4 RL

对于这种情况，我们需要将调整节点（4节点）的右子节点（6节点）进行一次右旋，然后对调整节点（4节点）进行一次左旋，如下

小结

AVL的调整策略有四种，LL、LR、RR、RL，其中LL和RR可以分为外侧调整，LR、RL可以分为内侧调整。对于外侧只需要进行一次单旋操作。对于内侧需要进行双旋，其中第一次将其变为外侧，第二次调整为AVL树

四、总结

本篇文章讲解了平衡二叉查找树和AVL树的概念，重点讲解了AVL树的调整策略，其中需要重点掌握的是旋转操作

好了，本文到此就结束了，下一篇文章将讲解红黑树