AVL树
文章目录
- AVL树
- 一、AVL树
- 1.特点
- 2.操作
- 旋转
- 插入
- 删除
- 查找
一、AVL树
在计算机科学中,AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。1.特点
AVL树本质上还是一棵二叉搜索树,它的特点是: 1.本身首先是一棵二叉搜索树。 2.带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。 也就是说,AVL树,本质上是带了平衡功能的二叉查找树(二叉排序树,二叉搜索树)。2.操作
旋转
AVL树的基本操作一般涉及运做同在不平衡的二叉查找树所运做的同样的算法。但是要进行预先或随后做一次或多次所谓的"AVL 旋转"。 假设由于在二叉排序树上插入结点而失去平衡的最小子树根结点的指针为a(即a是离插入点最近,且平衡因子绝对值超过1的祖先结点),则失去平衡后进行进行的规律可归纳为下列四种情况:单向右旋平衡处理LL:由于在*a的左子树根结点的左子树上插入结点,*a的平衡因子由1增至2,致使以*a为根的子树失去平衡,则需进行一次右旋转操作;
单向左旋平衡处理RR:由于在*a的右子树根结点的右子树上插入结点,*a的平衡因子由-1变为-2,致使以*a为根的子树失去平衡,则需进行一次左旋转操作;
双向旋转(先左后右)平衡处理LR:由于在*a的左子树根结点的右子树上插入结点,*a的平衡因子由1增至2,致使以*a为根的子树失去平衡,则需进行两次旋转(先左旋后右旋)操作。
双向旋转(先右后左)平衡处理RL:由于在*a的右子树根结点的左子树上插入结点,*a的平衡因子由-1变为-2,致使以*a为根的子树失去平衡,则需进行两次旋转(先右旋后左旋)操作。


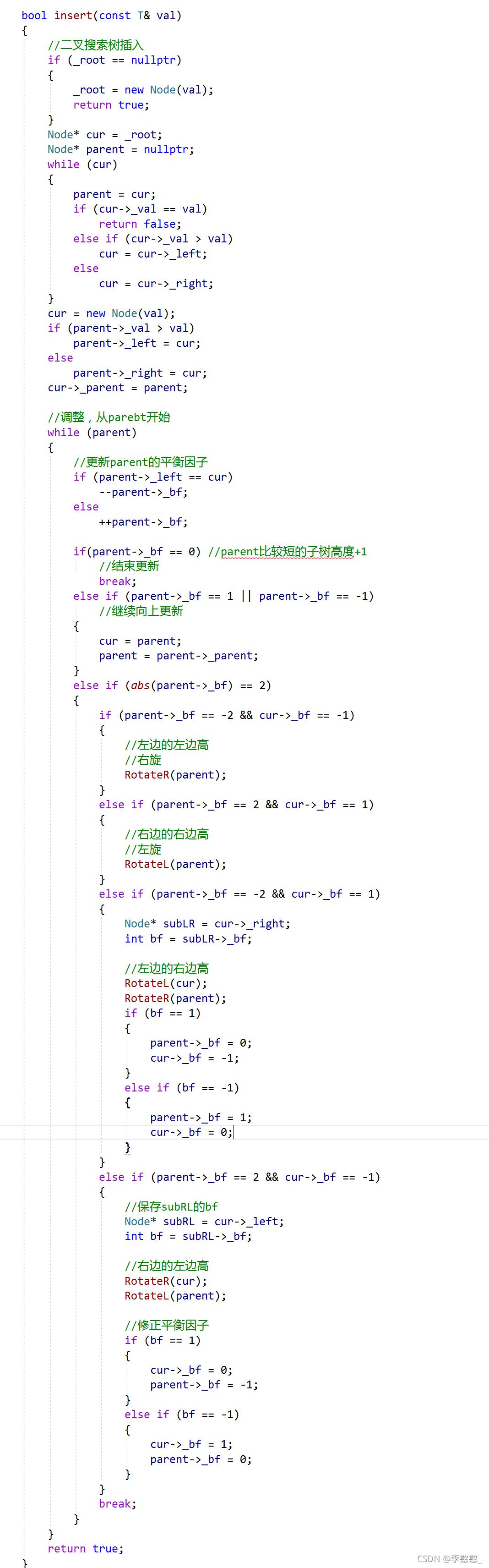
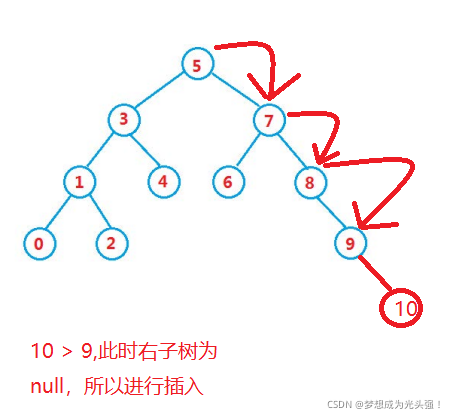
插入
向AVL树插入可以通过如同它是未平衡的二叉查找树一样把给定的值插入树中,接着自底向上向根节点折回,于在插入期间成为不平衡的所有节点上进行旋转来完成。因为折回到根节点的路途上最多有 1.5 乘 log n 个节点,而每次 AVL 旋转都耗费恒定的时间,插入处理在整体上耗费 O(log n) 时间。 在平衡的的二叉排序树Balanced BST上插入一个新的数据元素e的递归算法可描述如下: 若BBST为空树,则插入一个数据元素为e的新结点作为BBST的根结点,树的深度增1; 若e的关键字和BBST的根结点的关键字相等,则不进行; 若e的关键字小于BBST的根结点的关键字,而且在BBST的左子树中不存在和e有相同关键字的结点,则将e插入在BBST的左子树上,并且当插入之后的左子树深度增加(+1)时,分别就下列不同情况处理之:BBST的根结点的平衡因子为-1(右子树的深度大于左子树的深度,则将根结点的平衡因子更改为0,BBST的深度不变; BBST的根结点的平衡因子为0(左、右子树的深度相等):则将根结点的平衡因子更改为1,BBST的深度增1; BBST的根结点的平衡因子为1(左子树的深度大于右子树的深度):则若BBST的左子树根结点的平衡因子为1:则需进行单向右旋平衡处理,并且在右旋处理之后,将根结点和其右子树根结点的平衡因子更改为0,树的深度不变; 若e的关键字大于BBST的根结点的关键字,而且在BBST的右子树中不存在和e有相同关键字的结点,则将e插入在BBST的右子树上,并且当插入之后的右子树深度增加(+1)时,分别就不同情况处理之。