【算法修炼】二叉搜索树

article/2025/8/19 6:30:25

学习自：https://labuladong.gitee.io/algo/2/19/26/

二叉搜索树

      • 一、BST的中序遍历
        • 230、二叉搜索树中第k小的元素（中等）
        • 1038、从二叉搜索树到更大和树（中等）
      • 二、判断BST的合法性
        • ※98、验证二叉搜索树（中等）
        • ※※99、恢复二叉搜索树（困难）
        • 700、二叉搜索树中的搜索（简单）
      • 三、BST的插入、删除操作
        • BST中插入一个数
        • ※701、二叉搜索树中的插入操作（中等）
        • BST中删除一个数
        • ※450、删除二叉搜索树中的节点（简单）
      • 四、BST的重构问题
        • ※108、将有序数组转换为二叉搜索树（简单）
        • ※1382、将二叉搜索树变平衡（中等）
        • ※109、有序链表转换二叉搜索树（中等）
      • 五、如何计算所有有效 BST
        • ※※96、不同的二叉搜索树（中等）
        • ※95、不同的二叉搜索树Ⅱ（中等）
        • ※1373、二叉搜索子树的最大键值和（困难）

前面用了两篇博客，讲了二叉树的相关题目和解法，后面这几篇主要对二叉搜索树（Binary Search Tree）BST，进行讲解。

一、BST的中序遍历

BST 的特性大家应该都很熟悉了：
1、对于 BST 的每一个节点 node，左子树节点的值都比 node 的值要小，右子树节点的值都比 node 的值大。
2、对于 BST 的每一个节点 node，它的左侧子树和右侧子树都是 BST。

直接基于 BST 的数据结构有 AVL 树，红黑树等等，拥有了自平衡性质，可以提供 logN 级别的增删查改效率；还有 B+ 树，线段树等结构都是基于 BST 的思想来设计的。

就拿搜索某一个元素来说，BST 能够在对数时间找到该元素的根本原因还是在 BST 的定义里，左子树小右子树大嘛，所以每个节点都可以通过对比自身的值判断去左子树还是右子树搜索目标值，从而避免了全树遍历，达到对数级复杂度。

从做算法题的角度来看 BST，除了它的定义，还有一个重要的性质：BST 的中序遍历结果是有序的（升序），这个很简单，因为BST的特性就这么要求的。

230、二叉搜索树中第k小的元素（中等）

在这里插入图片描述
根据BST的特性来做就行。

class Solution {List<Integer> tmp = new LinkedList<>();public int kthSmallest(TreeNode root, int k) {// 说了是二叉搜索树BST，二叉搜索树的中序遍历一定是有序（从小到大）traverse(root);return tmp.get(k - 1);}void traverse(TreeNode root) {if (root == null) return;traverse(root.left);// 中序位置tmp.add(root.val);traverse(root.right);// 后序位置}
}

1038、从二叉搜索树到更大和树（中等）

在这里插入图片描述
每个节点更新为：大于或等于该节点值的所有节点值的和，那意思是需要从大到小遍历所有结点的同时，记录全局和，还要在这个过程中修改结点数值，如何在一个函数中同时实现上面操作？还是回到BST的特性，中序遍历得到的结果是从小到大排列的，那我需要从大到小呢？那就把遍历顺序调转一下不就行了，先遍历右再根，再左，同时记录全局和，在中序位置修改当前结点值即可，因为我们求的全局和，是在中序遍历的时候得到的。

class Solution {public TreeNode bstToGst(TreeNode root) {traverse(root);return root;}int sum = 0;void traverse(TreeNode root) {if (root == null) return;// 调换中序遍历位置traverse(root.right);sum += root.val;root.val = sum;traverse(root.left);}
}

二、判断BST的合法性

BST 的特性大家应该都很熟悉了：
1、对于 BST 的每一个节点 node，左子树节点的值都比 node 的值要小，右子树节点的值都比 node 的值大。
2、对于 BST 的每一个节点 node，它的左侧子树和右侧子树都是 BST。

先来看看这个代码是否正确？

boolean isValidBST(TreeNode root) {if (root == null) return true;if (root.left != null && root.val <= root.left.val)return false;if (root.right != null && root.val >= root.right.val)return false;return isValidBST(root.left)&& isValidBST(root.right);
}

在这里插入图片描述
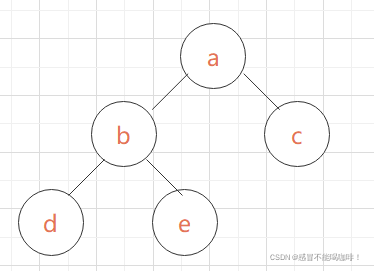
显然是不正确的，对于上面这幅图，上面的代码只check了当前结点的左右孩子，但BST要求的是当前节点的左右子树满足要求，也即当前结点的左子树的所有值都应该小于当前节点的值，右子树的值都应该大于当前值。上面的图很明显不是。

问题是，对于某一个节点 root，他只能管得了自己的左右子节点，怎么把 root 的约束传递给左右子树呢？

可以通过函数传参的方式，给出当前结点的最大值、最小值限定。

boolean isValidBST(TreeNode root) {return isValidBST(root, null, null);
}
/* 限定以 root 为根的子树节点必须满足 max.val > root.val > min.val */
boolean isValidBST(TreeNode root, TreeNode min, TreeNode max) {// base caseif (root == null) return true;// 若 root.val 不符合 max 和 min 的限制，说明不是合法 BSTif (min != null && root.val <= min.val) return false;if (max != null && root.val >= max.val) return false;// 限定左子树的最大值是 root.val，右子树的最小值是 root.valreturn isValidBST(root.left, min, root) && isValidBST(root.right, root, max);
}

其实思路很简单，记录下当前节点的左右子树的最大值、最小值，作为参数，因为不能够只比较左右节点。

父节点只能限制左子节点的最大值（左子节点的最小值还需要靠之前的记录），只能限制右子节点的最小值（右子节点的最大值还需要靠之前的记录）

※98、验证二叉搜索树（中等）

在这里插入图片描述

class Solution {public boolean isValidBST(TreeNode root) {return check(root, null, null);}boolean check(TreeNode root, TreeNode maxNode, TreeNode minNode) {if (root == null) return true;if (maxNode != null && root.val >= maxNode.val) return false;if (minNode != null && root.val <= minNode.val) return false;return check(root.left, root, minNode) && check(root.right, maxNode, root);}
}

※※99、恢复二叉搜索树（困难）

在这里插入图片描述
我们知道BST的中序遍历一定是有序的，那如果我们在中序遍历的过程中发现了逆序的情况，例如：3 2 1，显然存在着3 2和2 1两对逆序，我们只需要交换1、3即可。还有一种情况：例如：2 3 1（这种不满足题意，因为只有两个节点的值被错误的交换），例如：1 3 2（中序序列），只有一对逆序对（3 2），直接交换3 2即可。那就是说，无论出现哪种错误，我们只需要交换两个节点的值，我们可以用节点记录下出现错误的节点，然后在进行值的交换即可，当然找到出现错误的节点，得靠中序遍历。
在这里插入图片描述

关键点在于有两种错误情况，第一种需要找到第二次错误的地方，而第二种只用找到第一次错误的地方，但我们并不知道究竟是有几次错误，所以必须得遍历完所有节点。

图源：https://leetcode-cn.com/problems/recover-binary-search-tree/solution/tu-jie-hui-fu-yi-ge-er-cha-sou-suo-shu-by-hyj8/

class Solution {TreeNode err1 = null;TreeNode err2 = null;TreeNode prev = null;public void recoverTree(TreeNode root) {traverse(root);// 交换两个错误位置int tmp = err1.val;err1.val = err2.val;err2.val = tmp;}void traverse(TreeNode root) {if (root == null) return;traverse(root.left);// 中序位置对于BST来说是有序的if (prev != null && prev.val >= root.val) {if (err1 == null) {err1 = prev;}// 不能写成if elseif (err1 != null) {err2 = root;}}// 记录前一个结点prev = root;traverse(root.right);}
}

700、二叉搜索树中的搜索（简单）

在这里插入图片描述

class Solution {TreeNode ans;public TreeNode searchBST(TreeNode root, int val) {traverse(root, val);return ans;}void traverse(TreeNode root, int val) {if (root == null) {return;}traverse(root.left, val);// 以该节点为根，那不就只有在中序位置时能够遍历到根？// 那就直接在中序位置记录ans就行if (root.val == val) {ans = root;return;}traverse(root.right, val);}
}

但上面这样写，还不够，我们可以利用BFS的特性，左小右大，利用二分的思想去找。

class Solution {public TreeNode searchBST(TreeNode root, int val) {return traverse(root, val);}TreeNode traverse(TreeNode root, int val) {if (root == null) {return null;}// 利用二分的思想if (root.val > val) {return traverse(root.left, val);} else if (root.val < val) {return traverse(root.right, val);} else {return root;}}
}

三、BST的插入、删除操作

BST中插入一个数

插入 = 找位置 + 插入数，找位置简单，利用BST的性质，二分找，插入数也简单，new一个TreeNode即可。

class Solution {public TreeNode insertIntoBST(TreeNode root, int val) {if (root == null) {// 找到插入位置了return new TreeNode(val);}// 寻找插入位置if (root.val < val) {root.right = insertIntoBST(root.right, val);} else if (root.val > val) {root.left = insertIntoBST(root.left, val);}return root;}
}

※701、二叉搜索树中的插入操作（中等）

在这里插入图片描述
在这里插入图片描述
我们这里不以题目中第二种方法来插入，而是第一种，找边界位置。

class Solution {public TreeNode insertIntoBST(TreeNode root, int val) {if (root == null) {// 找到插入位置了return new TreeNode(val);}if (root.val < val) {// 比根节点大，只能放右边root.right = insertIntoBST(root.right, val);} else if (root.val > val) {// 比根节点小，只能放左边root.left = insertIntoBST(root.left, val);}return root;}
}

BST中删除一个数

删除 = 找位置 + 删除，可以写出这样的代码：

class Solution {public TreeNode deleteNode(TreeNode root, int key) {if (root.val == key) {// 找到位置进行删除} else if (root.val > key) {// 比当前key大，去左子树找deleteNode(root.left, key);} else {// 比当前key小，去右子树找deleteNode(root.right, key);}}
}

问题就在于，删除节点，节点所在的位置不好说呀！

图源：https://labuladong.gitee.io/algo/2/19/27/
第一种情况，位于叶子节点，那就直接return null

在这里插入图片描述

if (root.left == null && root.right == null) return null;

图源：https://labuladong.gitee.io/algo/2/19/27/

第二种情况，只有一个非空子节点，那么它要让这个孩子接替自己的位置。
在这里插入图片描述

// 排除第一种情况的前提下
if (root.left == null) return root.right;
if (root.right == null) return root.left;

第三种情况，既有左孩子，又有右孩子，为了不破坏 BST 的性质，必须找到左子树中最大的那个节点，或者右子树中最小的那个节点来接替自己（这里以第二种方法来讲），再删除右子树的最小节点即可。
图源：https://labuladong.gitee.io/algo/2/19/27/

在这里插入图片描述

if (root.left != null && root.right != null) {// 找到当前节点的右子树的最小节点TreeNode minNode = findMin(root.right);// 修改根节点值root.val = minNode.val;// 转去删除右子树的最小节点// 注意，题目上写的是swap，但实际并没有实现swap，而是用的val值替换root.right = deleteNode(root.right, minNode.val);
}

这个找最小节点怎么找呢？BST的特性，最左边的节点，一定是最小的，所以一直往左子节点遍历，直到最后遍历完即得到结果。

也可以通过类似于链表删除节点的方式，来删除节点：

	// 处理情况 3// 获得右子树最小的节点TreeNode minNode = getMin(root.right);// 删除右子树最小的节点root.right = deleteNode(root.right, minNode.val);// 用右子树最小的节点替换 root 节点minNode.left = root.left;minNode.right = root.right;root = minNode;

※450、删除二叉搜索树中的节点（简单）

在这里插入图片描述

class Solution {public TreeNode deleteNode(TreeNode root, int key) {if (root == null) return null;if (root.val == key) {if (root.left == null && root.right == null) return null;else if (root.left == null) return root.right;else if (root.right == null) return root.left;else {// 第三种情况// 找到右子树的最小值TreeNode minNode = findMin(root.right);root.val = minNode.val;// 更新完根节点，还要把右子树的最小节点删除，还是用这个函数把这个最小节点删除// 这个最小节点一定是叶子节点root.right = deleteNode(root.right, minNode.val);}} else if (root.val > key) {// 比key值大，找左子树root.left = deleteNode(root.left, key);} else {// 比key值小，找右子树root.right = deleteNode(root.right, key);}return root;}TreeNode findMin(TreeNode root) {while (root.left != null) {// BST树的特性，最左边的一定是最小的root = root.left;}return root;}
}

四、BST的重构问题

※108、将有序数组转换为二叉搜索树（简单）

在这里插入图片描述
注意还要保证是高度平衡的二叉搜索树，首先是要为二叉搜索树，跟之前构建二叉树的方法一样，也是通过限定数组的左右位置，来递归构建二叉搜索树。
在这里插入图片描述
先是要确定根，二叉搜索树的根只要左子树的所有节点小于它的值，右子树的所有节点的值都大于它的值即可，所以二叉搜索树的根可以在任何位置（数组是有序的），这样也能递归构建满足条件的二叉搜索树，问题在于，如何保证高度平衡（左右子树高度差 <= 1），那这就对根节点位置有要求了，必须取数组的中间位置！（偶数个数时，取中间第一个第二个无影响）

class Solution {public TreeNode sortedArrayToBST(int[] nums) {// 通过区分开左右区间进行求解return build(nums, 0, nums.length - 1);}TreeNode build(int[] nums, int leftSize, int rightSize) {if (leftSize > rightSize) return null;// 找正中间的数字作为根节点int idx = (leftSize + rightSize) / 2;TreeNode root = new TreeNode(nums[idx]);// 跟之前二叉树建树一样的方法root.left = build(nums, leftSize, idx - 1);root.right = build(nums, idx + 1, rightSize);return root;}
}

下面这道题同样用到了上面的方法，只是需要自己去获取有序数组

※1382、将二叉搜索树变平衡（中等）

在这里插入图片描述
如果只涉及查询，不要用LinkedList！

中序遍历构造有序数组，用有序数组递归构造平衡BST

class Solution {List<Integer> nodes = new ArrayList<>();public TreeNode balanceBST(TreeNode root) {traverse(root);// 获取到了有序数组，这个问题就转换为了：108、将有序数组转换为二叉搜索树int sz = nodes.size();return build(0, sz - 1);}// 中序遍历获取BST数组void traverse(TreeNode root) {if (root == null) return;traverse(root.left);// 中序遍历位置nodes.add(root.val);traverse(root.right);}// 根据有序数组构建高度平衡的BSTTreeNode build(int leftSize, int rightSize) {if (leftSize > rightSize) return null;// 找到根节点下标int idx = (leftSize + rightSize) / 2;// 递归构建高度平衡的BSTTreeNode root = new TreeNode(nodes.get(idx));root.left = build(leftSize, idx - 1);root.right = build(idx + 1, rightSize);return root;}
}

※109、有序链表转换二叉搜索树（中等）

在这里插入图片描述
把有序数组换成了有序链表，链表如何找中间节点？（快慢指针），再限定出具体的左右节点位置即可。这三道题其实本质是一样的，通过确定中间节点位置，再限定出左右节点范围。

class Solution {public TreeNode sortedListToBST(ListNode head) {if (head == null) return null;return build(head, null);}TreeNode build(ListNode head, ListNode tail) {if (head == tail) return null;// 快慢指针找链表中点ListNode fast = head;ListNode slow = head;while (fast != tail && fast.next != tail) {fast = fast.next.next;slow = slow.next;// 快指针走两步，慢指针走一步}// 此时慢指针指向中间位置TreeNode root = new TreeNode(slow.val);// 同BST的其它建树题目，需要限定出左右位置root.left = build(head, slow);root.right = build(slow.next, tail);return root;}
}

五、如何计算所有有效 BST

※※96、不同的二叉搜索树（中等）

在这里插入图片描述
解析源：https://mp.weixin.qq.com/s/kcwz2lyRxxOsC3n11qdVSw
在这里插入图片描述

左子树{1,2}，有两种BST组合方式，右子树{4,5}，有两种BST组合方式，所以以3作为根节点的BST个数 = 2 * 2 = 4，注意，这里说的组合是指构造出BST的组合方式，而不是排列组合的组合。
在这里插入图片描述
因为题目要求为：求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 ，就可以以每一个节点为根节点去找，这样当前节点的左边一定是作为左子树，右边一定作为右子树，本质是找左右边的组合数乘积。

class Solution {public int numTrees(int n) {return count(1, n);}public int count(int left, int right) {// 空节点 和 只有一个节点的情况，都返回1if (left >= right) return 1;int ans = 0;for (int i = left; i <= right; i++) {  // 遍历所有可能父节点// 看以当前节点为父节点的左、右子节点的组合方式有多少种int leftCount = count(left, i - 1);  // 框出左子节点区间int rightCount = count(i + 1, right);  // 框出右子节点区间ans += leftCount * rightCount;  // 计算当前根节点下的可能BST种类数}return ans;}
}

上面的代码时间效率不高，因为存在重复计算的问题，需要用备忘录记录计算过的结果。备忘录的下标由当前状态决定，而当前状态只由left和right，左右区间决定。

class Solution {int[][] table;public int numTrees(int n) {table = new int[n + 1][n + 1];return count(1, n);}public int count(int left, int right) {if (left > right) return 1; // 为空节点的情况// 已经算过了if (table[left][right] != 0) return table[left][right];int ans = 0;for (int i = left; i <= right; i++) {int leftCount = count(left, i - 1);int rightCount = count(i + 1, right);ans += leftCount * rightCount;}// 记录下当前结果table[left][right] = ans;return ans;}
}

这一题还可以转换成DP问题，关键是要找到如何转换？

问题在于把当前n个数，1 - n都能够当作根节点，然后去遍历以当前 i 作为根节点的左右子节点能够构成的BST数目，左右BST子树的组合乘积，即为当前 i 作为根节点的结果。

dp[i]表示，1-i 能够构成BST的组合种类数

import java.util.*;
public class Main {public static void main(String[] args) {Scanner scan = new Scanner(System.in);int n = scan.nextInt();int[] dp = new int[19 + 1];dp[0] = 1;  // 避免乘积=0dp[1] = 1;  // 一个节点只有一种构造方式for (int i = 2; i <= n; i++) {  // 遍历1-n的nfor (int j = 1; j <= i; j++) {  // 枚举1-i中每个数(节点)作为根节点的情况// 1 2 3，2 作为根节点，划分出1 3左右孩子// 3 作为根节点，就没有右孩子，剩下的全是左孩子// 左右子节点能够构成的BST的个数的乘积dp[i] += dp[j - 1] * dp[i - j];  // j - 1左子树, i - j右子树}}System.out.println(dp[n]);}
}

上一道题只是求个数，下面需要把每个搜索树都求出来。

※95、不同的二叉搜索树Ⅱ（中等）

在这里插入图片描述
明白了上道题构造合法 BST 的方法，这道题的思路也是一样的：

1、穷举root节点的所有可能。
2、递归构造出左右子树的所有合法 BST。
3、给root节点穷举所有左右子树的组合。

class Solution {public List<TreeNode> generateTrees(int n) {return build(1, n);}List<TreeNode> build(int left, int right) {List<TreeNode> ans = new LinkedList<>();if (left > right) {ans.add(null);return ans;}// 枚举每一个节点作为根节点的情况for (int i = left; i <= right; i++) {// 获取左子树的BST组合情况List<TreeNode> leftList = build(left, i - 1);// 获取右子树的BST组合情况List<TreeNode> rightList = build(i + 1, right);for (TreeNode t1 : leftList) {for (TreeNode t2 : rightList) {// 将左右子节点和根节点组合TreeNode root = new TreeNode(i);root.left = t1;root.right = t2;ans.add(root);}}}return ans;}
}

个人觉得，递归更考察对问题的宏观把握能力，因为你真的很难把递归的每一步想清楚，只可能把整个问题拆分成几个部分，然后考虑一下边界情况，这就是能做的事情，其余的就是相信这个递归函数，然后求解得到正确答案。

※1373、二叉搜索子树的最大键值和（困难）

在这里插入图片描述
注意，本题给的是二叉树，也就是说需要自己判断是否存在二叉搜索树。

注意下面这个例子，因为根节点为空也算BST，所以最大和为0。
在这里插入图片描述

摘自：https://labuladong.gitee.io/algo/2/19/29/
那么我们想计算子树中 BST 的最大和，站在当前节点的视角，需要做什么呢？

1、我肯定得知道左右子树是不是合法的 BST，如果这俩儿子有一个不是 BST，以我为根的这棵树肯定不会是 BST，对吧。

2、如果左右子树都是合法的 BST，我得瞅瞅左右子树加上自己还是不是合法的 BST 了。因为按照 BST 的定义，当前节点的值应该大于左子树的最大值，小于右子树的最小值，否则就破坏了 BST 的性质。

3、因为题目要计算最大的节点之和，如果左右子树加上我自己还是一棵合法的 BST，也就是说以我为根的整棵树是一棵 BST，那我需要知道我们这棵 BST 的所有节点值之和是多少，方便和别的 BST 争个高下，对吧。

首先需要判断BST，判断BST就需要记录遍历过程中的minNode和maxNode，只有左右子树是BST，并且根节点大于左子树的最大节点值，小于右子树的最小节点值，才能说这个树是BST。光判断BST还不够，还需要求这个BST的所有节点值之和，所以还需要记录BST的节点值之和。

综上，一共需要四个参数，是否为BST、当前BST子树的最小值、当前BST子树的最大值、当前BST子树的所有节点值之和（因为不是BST就不用考虑剩余内容）

class Solution {int max = Integer.MIN_VALUE;public int maxSumBST(TreeNode root) {traverse(root);return Math.max(max, 0);}// 函数返回 int[]{isBST, min, max, sum}// min，max是当前BST树的最大最小值int[] traverse(TreeNode root) {if (root == null) {// 为空，是BST，sum = 0return new int[] {1, Integer.MAX_VALUE, Integer.MIN_VALUE, 0};}int[] leftNode = traverse(root.left);int[] rightNode = traverse(root.right);int[] ans = new int[4];// 在后序位置，前面两个值都能够获取// 左右子树都满足BST，再看加上根节点是否满足BSTif (leftNode[0] == 1 && rightNode[0] == 1 && root.val > leftNode[2] && root.val < rightNode[1]) {// 当前BST树一定是BSTans[0] = 1;// 求当前BST树的最大值、最小值ans[1] = Math.min(leftNode[1], root.val);ans[2] = Math.max(rightNode[2], root.val);// 求当前BST的最大键值和int sum = leftNode[3] + rightNode[3] + root.val;ans[3] = sum;max = Math.max(max, sum);}return ans;}
}

有很多同学可能会有疑问，这里为什么是min、max，如果以当前节点为根节点，左子树的最小值一定是当前BST树的最小值呀？右子树同样是这样，取min和max的原因与我们对空节点的初始化值有关！
在这里插入图片描述

在这里插入图片描述


http://chatgpt.dhexx.cn/article/577OWB1h.shtml

相关文章

数据结构（C语言）-树

数据结构（C语言）-树

树 一、树1、树的定义2、树的基本术语3、树结构和线性结构的比较 二、二叉树1、二叉树的定义2、二叉树的形态与树的形态3、二叉树的性质4 、二叉树的存储结构5、遍历二叉树6、二叉树的其他操作7、线索二叉树 三、树与二叉树的转换1、树转换成二叉树2、二叉树变树 四、哈夫曼树1…
阅读更多...
【数据结构与算法】程序内功篇六--树

【数据结构与算法】程序内功篇六--树

程序内功篇六--树 一、树1、树的含义2、树的特点(选看)3、树的逻辑结构 二、二叉树1、二叉树的含义2、二叉树性质3、二叉树-顺序存储4、二叉树-链式存储5、二叉树的遍历6、二叉树创建与遍历C程序的实现&#xff08;1&#xff09;二叉树的创建&#xff08;2&#xff09;前序遍历…
阅读更多...
数据结构---与树相关的知识

数据结构---与树相关的知识

与树有关的一系列知识: 树,二叉树,满二叉树,完全二叉树,文章还没完,我会后序补充的 一: 树(了解就行)1.1 概念1.2 一些与树相关的重要概念1.3 树的表示形式 二: 二叉树(非常重要,重点掌握)2.1 概念2.2 两种特殊的二叉树2.2.1 满二叉树2.2.2 完全二叉树 2.3 二叉树的性质2.4 二叉…
阅读更多...
Java数据结构--树1

Java数据结构--树1

Java数据结构--树 一、二叉树入门1.1 树的基本定义1.2 树的相关术语1.3 二叉树的基本定义1.4 二叉查找树的创建1.4.1 二叉树的结点类1.4.2 二叉查找树API设计1.4.3 二叉查找树实现1.4.4 二叉查找树其他便捷方法1.4.4.1 查找二叉树中最小的键1.4.4.2 查找二叉树中最大的键 1.5 二…
阅读更多...
树 一

树 一

文章目录 1.查找二分查找判定树 2. 树(Tree)2.1 树的术语2.2树的表示&#xff1a;儿子兄弟表示法 3. 二叉树&#xff08;Binary Tree&#xff09;3.1 特殊结构二叉树3.2 二叉树的性质3.3 二叉树的存储3.4二叉树的遍历 分层次组织管理上更有效地操作。 1.查找 静态查找&#xf…
阅读更多...
树一：邂逅入门篇

树一：邂逅入门篇

一、树的概念 树是一种典型的非线性结构&#xff0c;是表达有层次特性的图结构的一种方法。 1.1 基本术语 术语描述空树当n0 时称为空树。根结点根结点是一个没有双亲结点的结点。一棵树最多一个。例如&#xff1a;A边结点之间的连线叶子结点没有孩子结点的结点。例如&#x…
阅读更多...
树一：定义及存储

树一：定义及存储

树的定义&#xff1a; 树是一种非线性的数据结构。树是由 n (n > 0) 个结点组成的有序集合。 如果 n 为0&#xff0c;称为空树&#xff1b;如果 n > 0, 则&#xff1a; 有一个结点称为根结点&#xff08;root&#xff09;&#xff0c;它有直接后继&#xff0c;但没有直接…
阅读更多...
mysql 创建索引规则

mysql 创建索引规则

1、表的主键、外键必须有索引&#xff1b; 2、数据量超过300的表应该有索引&#xff1b; 3、经常与其他表进行连接的表&#xff0c;在连接字段上应该建立索引&#xff1b; 4、经常出现在Where子句中的字段&#xff0c;特别是大表的字段&#xff0c;应该建立索引&#xff1b; 5、…
阅读更多...
mysql分区表之三：MySQL分区建索引,唯一索引

mysql分区表之三：MySQL分区建索引,唯一索引

介绍 mysql分区后每个分区成了独立的文件&#xff0c;虽然从逻辑上还是一张表其实已经分成了多张独立的表&#xff0c;从“information_schema.INNODB_SYS_TABLES”系统表可以看到每个分区都存在独立的TABLE_ID,由于Innodb数据和索引都是保存在".ibd"文件当中&#…
阅读更多...
分享mysql创建索引的3种方法

分享mysql创建索引的3种方法

大家应该都知道索引的建立对于MySQL数据库的高效运行是很重要的,索引可以大大提升MySQL的检索速度,下面这篇文章主要给大家介绍了关于mysql创建索引的3种方法,需要的朋友可以参考下 1、使用CREATE INDEX创建&#xff0c;语法如下&#xff1a; 1 CREATE INDEX indexName ON tab…
阅读更多...
js 监听浏览器刷新还是关闭事件

js 监听浏览器刷新还是关闭事件

// $(window).bind(beforeunload,function(){return 您输入的内容尚未保存&#xff0c;确定离开此页面吗&#xff1f;;}); // window.onbeforeunload function() { return "确定离开此页面吗&#xff1f;"; }; // function myFunction() {return "自定…
阅读更多...
浏览器刷新和页面手动为什么不一样？

浏览器刷新和页面手动为什么不一样？

Fiddler(2):AutoResponse修改返回结果_mb5fed6ec4336ce的技术博客_51CTO博客Fiddler(2):AutoResponse修改返回结果&#xff0c;前言怎么修改接口的返回数据呢步骤1.抓包&#xff0c;找到要拦截的请求&#xff0c;然后在AutoResponder中AddRule&#xff1a;2.在RuleEditor中的第…
阅读更多...
vue监听浏览器刷新和关闭事件，并在页面关闭/刷新前发送请求

vue监听浏览器刷新和关闭事件，并在页面关闭/刷新前发送请求

vue监听浏览器刷新和关闭事件&#xff0c;并在页面关闭/刷新前发送请求 1.需求背景&#xff1a;2.需求分析&#xff1a;3.实现方式&#xff1a;4.实现方式解析&#xff1a;1&#xff09;浏览器页面事件基础2&#xff09;在mounted监听beforeunload和unload事件 5.存在的问题/风…
阅读更多...
浏览器刷新和关闭时显示提示信息

浏览器刷新和关闭时显示提示信息

vue 刷新和关闭浏览器时显示提示信息 使用onbeforeunload事件 mounted() {window.onbeforeunload e > {e e || window.eventif (e) {e.returnValue 关闭提示}return 关闭提示}} }, beforeDestroy() {window.onbeforeunload null },如果是所有页面都需要页面销毁显示提…
阅读更多...
【Vue实用功能】Vue监听浏览器刷新和关闭事件

【Vue实用功能】Vue监听浏览器刷新和关闭事件

Vue监听浏览器刷新和关闭事件 在前端开发中&#xff0c;我们通常会遇到这样的需求&#xff0c;用户离开、刷新页面前&#xff0c;修改数据未进行保存操作&#xff0c;需要提示框提醒用户 效果实现 methods: {/** 在刷新和关闭之前询问 **/beforeRefreshClose() {let self t…
阅读更多...
vue监听浏览器刷新和关闭；

vue监听浏览器刷新和关闭；

注意&#xff1a;区分不了浏览器是触发了刷新还是关闭&#xff0c;而且提示的弹框是无法自定义的&#xff1b;如果有大佬有方法能区分&#xff0c;还请评论学习一下&#xff01;感谢&#xff01; 代码可直接复制&#xff1a; <template><div><div /></di…
阅读更多...
JS阻止浏览器刷新的方法

JS阻止浏览器刷新的方法

直接先给朋友们上阻止浏览器刷新的代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><meta http-equiv&quo…
阅读更多...
VSCODE同步浏览器刷新

VSCODE同步浏览器刷新

VSCODE同步浏览器刷新 安装插件 live server
阅读更多...
java中foreach的用法

java中foreach的用法

文章目录 前言语法用法用法1&#xff1a;输出一维数组用法2&#xff1a;输出二维数组foreach的局限性什么是索引 总结 前言 java中foreach,可以认为是增强版的for语句循环&#xff0c;它可以减少代码量&#xff0c;但是不是所有的foreach都可以代替for循环。 语法 foreach的…
阅读更多...
JAVA实现九九乘法表

JAVA实现九九乘法表

用java语言实现九九乘法表&#xff0c;这里使用的是for循环 public class NineNineDemo{public static void main(String[] args){int i1;//对行变量赋值int j1;//对列变量赋值for(i1;i<9;i){for(j1;j<i;j){//行变量外循环&#xff1b;列变量内循环System.out.print(i&q…
阅读更多...
推荐文章

Copyright @ 2022~2023