一丶概念以及特点

什么是二叉搜索树呢？

二叉搜索树就是二叉树的基础上对其进行一定规则的限制。即就是：二叉搜索树中任一节点的左子树的值都小于当前节点的值，右子树的值都大于当前节点的值。

也就是说：如果任一结点的左子树非空，则左子树的所有结点的值都小于根结点的值；如果任一结点的右子树非空，则右子树的所有结点的值都大于根结点的值。

这意味着什么呢？

意味着在中序遍历的情况下，二叉搜索树是一个单调递增的数组。

二丶相关操作

那么二叉搜索树这里，我们自己定义实现一个。其中每个节点的值我们用TreeMap的节点来表示。那么在这之前，我们是不是要先定义一个Map的接口，然后以此来实现其内部的部分属性。

public interface Map<K extends Comparable<K>,V> {//Entry<K, V> 是Map内部实现的用来存放<key, value>键值对映射关系的内部类public static class Entry<K,V>{K key;V value;//Key的获取K getKey(){return key;}//Value的获取V getValue(){return value;}//设置Value的方法V setValue(V value){V oldValue = this.value;this.value = value;return oldValue;}}//Map其中的一些内置方法public V put(K key, V value);public V get(K key);public V getOrDefault(K key, V value);public V remove(K key);public boolean containsKey(K key);public boolean containsValue(V value);public int size();
}

我们定义了Map接口之后，接下来我们就准备开始着手准备实现二叉搜索树。

定义TreeMap类

我们定义TreeMap类并且实现自己定义的Map接口后再初始化，这样我们就有了代码的初始版本，然后接下里的工作就是对一些主要的方法进行讲解。

public class TreeMap<K extends Comparable<K>,V> implements Map<K,V>{//定义TreeNode节点public static class TreeNode<K,V>{TreeNode left;TreeNode right;Map.Entry<K,V> kv;public TreeNode(K key,V value){kv = new Entry<>();kv.key = key;kv.value = value;}}//接着定义根节点TreeNode<K,V> root;int size = 0;//以下全部都是需要我们自己实现的方法@Overridepublic V put(K key, V value) {return null;}@Overridepublic V get(K key) {return null;}@Overridepublic V getOrDefault(K key, V value) {return null;}@Overridepublic V remove(K key) {return null;}@Overridepublic boolean containsKey(K key) {return false;}@Overridepublic boolean containsValue(V value) {return false;}@Overridepublic int size() {return 0;}
}

put()操作–插入节点

如果我们要插入一个节点，那么我们首先要根据key的值来确定对应的位置。
就比如下面这个二叉搜索树。

如果说，此时我们要插入节点的key值为10，那么我们该怎么办呢？

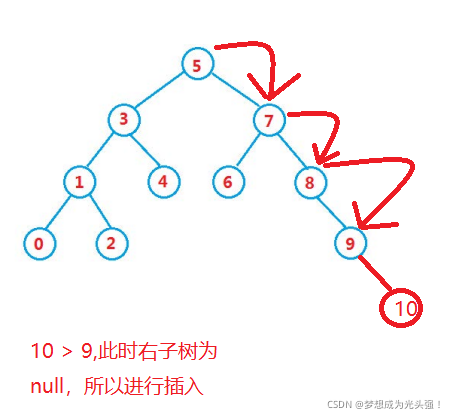
那么注意了，如果说我要插入的节点和已经有的节点的key值相同怎么办呢？
$key值相同，那么value值会被覆盖$

大致原理说清了，接下来给出代码实现：

@Overridepublic V put(K key, V value) {//这种是节点为null的情况if(root == null){root = new TreeNode<>(key,value);size++;return value;}//接下来对插入位置进行查找,如果下标的节点已经存在就覆盖，不存在的话就要用parent进行来进行标志插入TreeNode<K,V> cur = root;TreeNode<K,V> parent = null;while(cur != null){parent = cur;int fac = key.compareTo(cur.kv.key);//下标进行比较if(fac > 0) {cur = cur.right;}else if(fac < 0){cur = cur.left;}else{V oldValue = cur.kv.value;cur.kv.value = value;return oldValue;}}//要插入节点在树中不存在所以不存在覆盖这种情况，就有了以下对左右子树插入情况的判断int res = key.compareTo(parent.kv.key);TreeNode<K,V> fac = new TreeNode<>(key,value);if(res > 0){parent.right = fac;}else{parent.left = fac;}size++;return value;}

get()操作–得到key对应的value值

首先，如果要知道一个节点存不存在我们就要遍历这些节点了，但不是全部遍历，要根据其性质来。
get操作和put操作原理是一样的，但是呢：

get操作就单单是查找对应节点，如果找到了就返回true，没找到就是false。put操作也是查找对应节点，如果找到了对应节点就覆盖，没找到就插入就行。

@Overridepublic V get(K key) {TreeNode<K,V> cur = root;while(cur != null){int val = key.compareTo(cur.kv.key);if(val > 0){cur = cur.right;}else if(val < 0){cur = cur.left;}else{return cur.kv.value;}}return null;}

getOrDefault()操作

这个操作还是挺容易实现的，毕竟你只需要得到Key对应的value值是不是null，如果是null就返回你设置的值，不为null就返回其本身的值。其实也就是引用一下上面的get()方法。

@Overridepublic V getOrDefault(K key, V value) {//先定义本身的value值V node  = get(key);//如果为null就返回你传入的value值，不为null就返回本身的value值return node == null ? value : node;}

containsKey()操作–检查key是否存在

这个操作也就是对上面的操作加以引用和延伸。我们自己实现的话还是对put()这个方法加以改写。
这个方法的主要作用就是查看Key是否存在

public boolean containsKey(K key) {TreeNode<K,V> cur = root;while(cur != null) {int fac = key.compareTo(cur.kv.key);if(fac == 0){return true;}else if(fac > 0){cur = cur.right;}else{cur = cur.left;}}return false;}

containsValue()操作–检查value是否存在

想要看value值存不存在，那么就需要遍历整个二叉树。

	@Overridepublic boolean containsValue(V value) {return containsValue(value,root);}public boolean containsValue(V value,TreeNode<K,V> root) {TreeNode<K,V> cur = root;if(cur == null){return false;}if(cur.kv.value == value){return false;}return containsValue(value,root.left) || containsValue(value,root.right);}
}

这里为了尽量接近原有代码，不破坏其完整性，所以对方法进行了重载。

remove()操作–删除操作

首先如果说要删除一个节点，那我们肯定是要分情况讨论的。因为不可能一上去就直接乱删。那具体的删除情况根据子节点的不同可以分为以下几种。

1.当前节点是叶子结点
2.当前节点左子树为空
3.当前节点右子树为空
4.当前节点左右子树都在

先罗列出具体的分类，然后一个一个情况来进行讨论。
$在这里我们用cur来寻找并且标记要删除的节点，用parent来标$
$记其走过的上一个节点。$

思路

（1）叶子结点

如果是叶子结点，那么我们归并到情况2进行解决。
为什么可以这样做？那么继续往下走就好啦。

（2）左子树为空

如果说当前节点左子树为空，那么就证明只有右子树，这个时候就需要对当前节点所在位置进行判断。

1.该节点可能是根节点
2.该节点可能是其双亲节点的左子树
3.该节点可能是其双亲节点的右子树

对于上面的三种情况，我们按照如下方式来解决：

1.如果说当前节点为根节点，那么就让root指向它的右子树
2.如果说当前节点为其双亲节点的左子树，那么就是parent.left = cur.right
3.如果说当前节点为其双亲节点的右子树，那么就是parent.right = cur.right

所以如果说当前节点为叶子结点，那么这个时候它不论是其双亲节点的左子树还是右子树，最后它的位置肯定会置为空。
所以左子树为空的情况就直接解决了叶子结点为空的这种情况。

（3）右子树为空

如果说当前节点右子树为空，那么处理方法和左子树为空时候一样，要先清楚当前节点的位置。

1.要删除节点为根节点
2.该节点可能是其双亲节点的左子树
3.该节点可能是其双亲节点的右子树

那么对于以上的情况，我们怎样处理呢？

1.如果是根节点，那么就让root指向当前节点的左子树
2.如果是双亲节点的左子树,那么parent.left = cur.left
3.如果是双亲节点的右子树，那么parent.right = cur.left

（4）左右子树都在

那么如果说一个节点的左右子树都在，那么我们就要从这个节点开始找，找什么呢？

1.可以找左子树当中的最大值。
2.也可以找右子树当中的最小值。

找到之后怎么办呢？用找到的节点和待删除的节点进行交换。接下里就删除我们待删除的节点就好了。这里我们一般情况下是找右子树当中的最小值，也就是右子树当中最左侧的节点。

具体代码

@Overridepublic V remove(K key) {TreeNode<K,V> cur = root;TreeNode<K,V> parent = null;while(cur != null){int res = key.compareTo(cur.kv.key);if(res > 0){parent = cur;cur = cur.right;}else if(res < 0){parent = cur;cur = cur.left;}else{break;}}if(cur == null){return null;}V val = cur.kv.value;//那接下来待删除节点已经找到，开始进行删除if(cur.left == null){//左子树为空的情况if(parent == null){//如果是根节点root = cur.right;}else{//不是根节点if(cur == parent.left){parent.left = cur.right;}else{parent.right = cur.right;}}cur.right = null;}else if(cur.right == null){//右子树为空if(parent == null){root = cur.left;}else{if(parent == parent.left){parent.left = cur.left;}else{parent.left = cur.left;}}cur.left = null;}else{//左右子树都不为空TreeNode<K,V> fac = cur.right;parent = cur;while(fac.left != null){parent = fac;fac = fac.left;}cur.kv = fac.kv;//把右子树最左侧节点覆盖待删除节点if(parent.left == fac){parent.left = fac.right;}else{parent.right = fac.right;}}return val;}