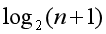有些图是网上找的,没有自己画

一: 树(了解就行)

1.1 概念

树是一种非线性的数据结构,它是由n(n>=0)个有限节点组成的一个具有层次关系的集合.
叫成树的原因: 看起来像是一棵倒着的树,它的根朝上,而叶子是朝下的.
树的一些特点:
a. 有一个特殊的节点,称为根节点,根节点没有前驱节点.
b. 除根节点外,其余的节点被分成M(M>0)个互不相交的集合T,T2,T3…Tm,其中每一个集合又是一棵与树类似的子树.
c. 一棵n个节点的树有n-1条边.
d. 除根节点外,每个节点有且仅有一个父节点
e. 子树是不能相交的.
f. 树是递归定义的.

1.2 一些与树相关的重要概念

节点的度: 一个节点含有子树的个数称为该节点的度
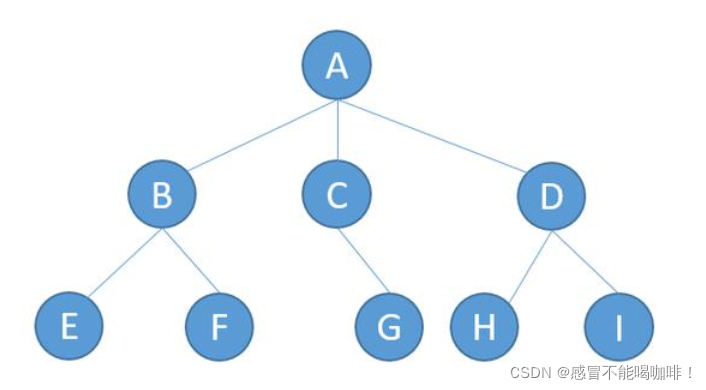
比如:上图中节点A的度为2,节点D的度为3.

树的度: 一颗树中,所有节点度的最大值称为树的度
比如:上图中树的度为3

叶子节点或终端节点: 度为0的节点称为叶子节点或者终端节点
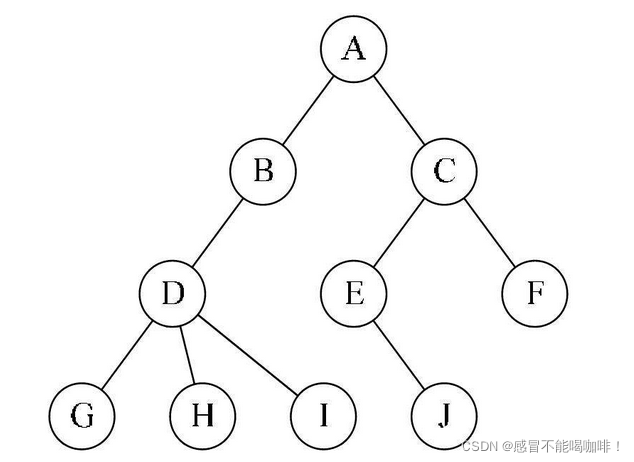
比如:上图中的叶子节点有:F,G,H,I,J.

双亲节点或父节点: 如果一个节点含有子节点,这个节点就称为子节点的父节点或者双亲节点.
比如:上图中的A是B,C的父节点.

孩子节点或子节点: 一个节点含有的子树的根节点称为该节点的子节点.
比如:上图中的B,C是A的孩子节点.

根节点: 树种没有双亲的节点.(位于食物链顶端的节点)
比如:上图中的A节点.

节点的层次: 从根开始定义起,根为第一层,根的子节点为第二层,依次类推

树的高度或深度: 树中节点的最大层次.
比如:上图中树的深度为4

非终端节点或分支节点: 度不为0的节点
比如:上图中的B,D节点

兄弟节点: 具有相同父节点的节点称为兄弟节点
比如:上图中的G,H,I节点

堂兄弟节点: 双亲在同一层的节点互为堂兄弟
比如:上图中的D,E节点

节点的祖先: 从根节点到该节点所经分支上的所有节点
比如:G节点的祖先节点是A,B,D节点.而A节点是所有节点的祖先节点.

子孙节点: 以某节点为根的子树中任一节点都称为该节点的子孙.
比如:上图中D节点的子孙节点是G,H,I.而所有节点都是A的子孙节点.

森林: 有m(m>0)棵互不相交的树组成的集合称为森林.

1.3 树的表示形式

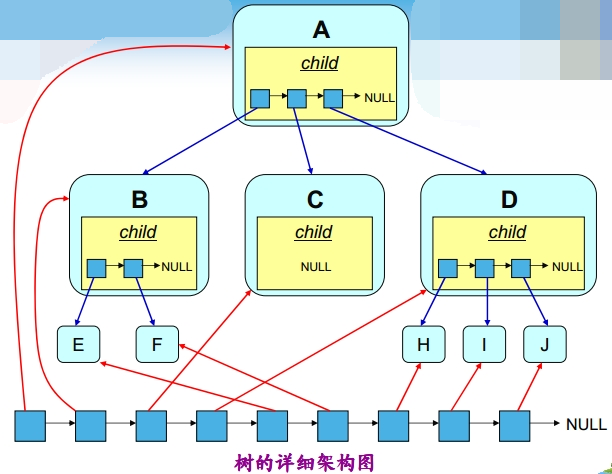
树有很多种表现形式,但是最常用的是这里的孩子兄弟表示法
a.双亲表示法

节点既要存储值域,还必须表示其双亲的位置.
优点: 快速知道该节点的双亲.
缺点: 无法快速知道该节点的孩子.

class Node{int value;		//存储的数据Node parent;	//指向父节点
}

b.孩子表示法

节点既要存储值域,还要表示与孩子之间的关系.
优点: 快速知道该节点的孩子.
缺点: 无法快速知道该节点的双亲

class Node{int value;		//存储的数据Node left;		//指向左孩子,常常代表左孩子为根的整棵左子树Node right;		//指向右孩子,常常代表右孩子为根的整棵右子树
}

c.孩子双亲表示法

将孩子表示法和双亲表示法结合起来了.

class Node{int value;		//存储的数据Node left;		//指向左孩子,常常代表左孩子为根的整棵左子树Node right;		//指向右孩子,常常代表右孩子为根的整棵右子树Node parent;	//当前节点的父节点.
}

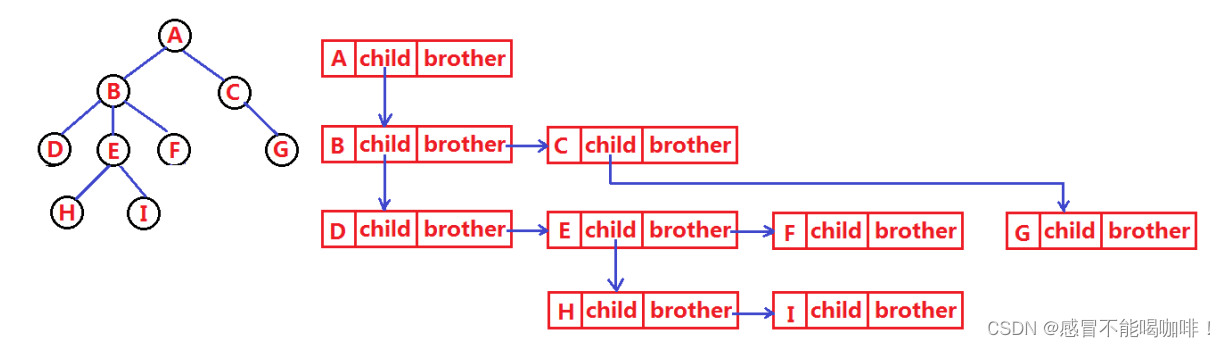
d.孩子兄弟表示法

在这个节点中,既要保存值域,还要保存下一个兄弟在哪一个位置.

class Node{int value;			//树中存储的数据Node firstChild;	//第一个孩子的引用Node nextBrother;	//下一个兄弟的引用
}

二: 二叉树(非常重要,重点掌握)

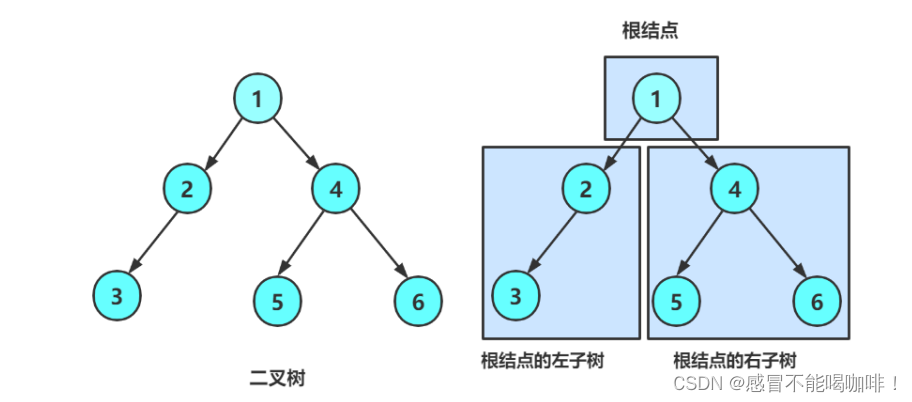
2.1 概念

满足: 1.为空树时,是二叉树 2.由根节点+左子树+右子树组成.

一棵二叉树是节点的一个有限集合:
a.集合可以为空: 表示这是一棵空树
b.不为空: 由一个根节点加上两棵分别称为左子树和右子树的二叉树组成
c.二叉树不存在度大于2的节点(此节点的孩子子节点个数只能<=2)
d.二叉树的子树有左右之分,次序不能颠倒,依次二叉树是有序树.

注意: 对于任意的二叉树都是由以下集中情况复合而成的.

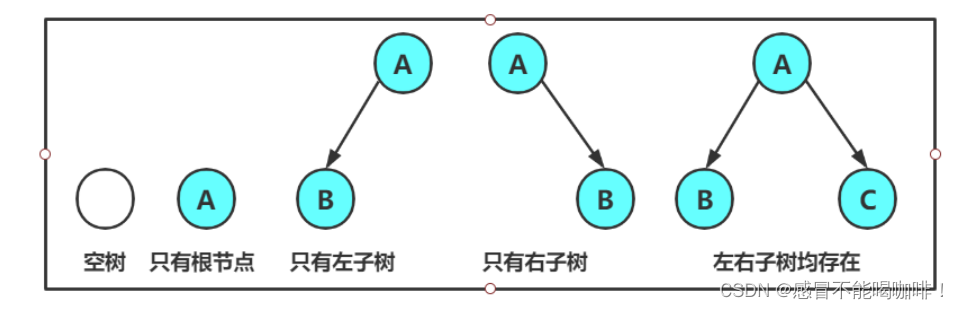
2.2 两种特殊的二叉树

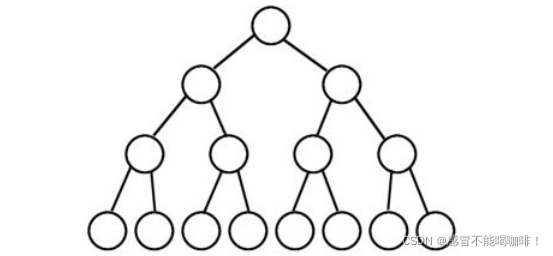
2.2.1 满二叉树

一棵二叉树,如果每层的节点数都能达到最大值,则这棵二叉树就是满二叉树.
如果一棵二叉树的层数为k,且它的节点数是(2^k)-1,则它也是满二叉树.

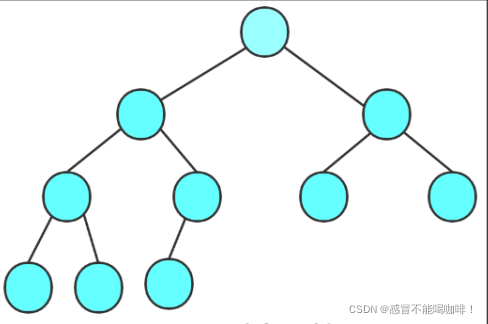
2.2.2 完全二叉树

完全二叉树是由满二叉树引出来的.满二叉树是一种特殊的完全二叉树.

设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到饱和(即1~h-1层为一个满二叉树)，第 h 层所有的结点都从左往右依次排列，这样的树就是完全二叉树。

完全二叉树

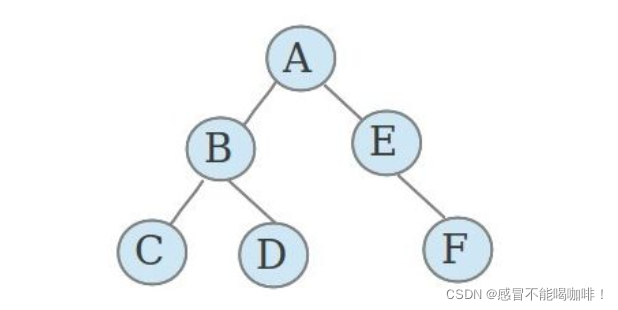
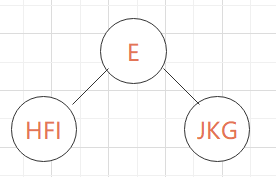
我们来举一个例子:看下面这张图,就不是完全二叉树,因为E节点只有F一个子节点，但是F子节点没有排在E节点的左边

2.3 二叉树的性质

1.若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有 2^(i-1) 个节点(i>0).
2.若规定只有根节点的二叉树的深度为1,则深度为k的文二叉树的最大节点数是 (2^k)-1(k>=0).
3.对任何一棵二叉树,如果其叶子几点个数为n0,度为2的非叶子节点个数为n2,则有n0=n2+1.
4.具有n个结点的完全二叉树的深度k为

向上取整
5.对于具有n个结点的完全二叉树，如果按照 从上至下从左至右 的顺序对所有节点从0开始编号，则对于序号为i的结点有：

• 若i>0，双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点
• 若2i+1<n，左孩子序号：2i+1，否则无左孩子
• 若2i+2<n，右孩子序号：2i+2，否则无右孩子

2.4 二叉树的基本操作

2.4.1手动快速创建一棵简单的二叉树

这段代码并不是创建二叉树的方式,真正创建二叉树方法后序会重点讲解.

//孩子表示法来表示二叉树.
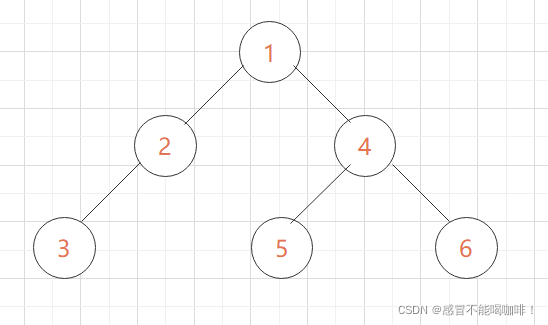
public class BinaryTree{public static class BTNode{BTNode left;	//引用当前孩子的左孩子BTNode right;   //引用当前孩子的右孩子int value;		//值域//有参构造方法BTNode(int value){this.value = value;}}private BTNode root;	//二叉树的根节点public void createBinaryTree(){BTNode node1 = new BTNode(1);	//创建节点node1,它的值为1BTNode node1 = new BTNode(2);BTNode node1 = new BTNode(3);BTNode node1 = new BTNode(4);BTNode node1 = new BTNode(5);BTNode node1 = new BTNode(6);root = node1;		    //根节点就是node1节点node1.left = node2;		//node1的左孩子是node2node1.right = node4;	//node1的右孩子是node4node2.left = node3;		//node2的左孩子是node3node4.left = node5;		//node4的左孩子是node5node4.right = node6;	//node5的右孩子是node6}
}

由以上代码创建出来的二叉树为下图所示:

2.4.2 二叉树的遍历

例图:

a. 前中后序遍历(递归操作)

学习二叉树结构,最简单的方式就是遍历.

遍历: 所谓遍历是指沿着某条路径搜索路线,依次对树中每个节点均做一次且仅做一次访问.
用N代表根节点,L代表根的左子树,R代表根的右子树.则有以下遍历方式 (用上图演示)

指的是对节点中的值域进行打印.
NLR:前序遍历----------------根节点---->根的左子树---->根的右子树
1–>2–>3–>4–>5–>6

public void preOrder(BtNode reeRoot){//先判断是否为空if(treeRoot==null){return;}//1.先遍历根节点System.out.print(treeRoot.value+" ");//2.再遍历根节点的左子树----->根节点的左子树也是二叉树(遍历根的左子树与遍历原树的规则相同)preOrder(treeRoot.left);		//递归遍历根的左子树//3.最后遍历根节点的右子树----->根的右子树也是二叉树(遍历根的右子树与遍历原树的规则相同)preOrder(treeRoot.right);	//递归遍历根的右子树
}

LNR:中序遍历----------------根的左子树---->根节点---->根的右子树
3–>2–>1–>5–>4–>6

public void inOrder(BtNode reeRoot){if(treeRoot==null){return;}inOrder(treeRoot.left);		System.out.print(treeRoot.value+" ");inOrder(treeRoot.right);	
}

LRN:后序遍历----------------根的左子树---->根的右子树---->根节点
3–>2–>5–>6–>4–>1

public void postOrder(BtNode reeRoot){if(treeRoot==null){return;}postOrder(treeRoot.left);		postOrder(treeRoot.right);	System.out.print(treeRoot.value+" ");
}

b. 前中后序遍历(非递归)

非递归采用的是List和栈的数据结构来进行实现的.
利用栈先进后出的特点来实现前中后序的遍历,再用list来接收节点的值,最后list中的数据就是遍历的结果.

注意：在下面我只给了前序遍历的讲解图，中序和后序遍历大家自己根据对前序遍历的理解，对应代码画一下，刚好作为一个思考和练习题。

前序遍历:

a.创建对象List和栈的对象为list,s.
b.用cur标记root节点,然后将cur进行入栈操作.
c.当栈不为空时,节点出栈然后用cur接收.
d.当cur不为空时,将此时cur节点的值add到list中.
e.然后判断此时的cur有没有右孩子,有的话就将右孩子进行入栈操作.然后cur指向左孩子
最后重复d过程,当cur为空时再从c过程开始执行.
最后list中存储的数据就是前序遍历的结果.文字可能看起来不怎么清楚,我们直接上图形.
大家一定要对照着下面的代码去看图,然后根据代码自己在纸上画一遍,才能更好的理解和掌握

当s不为空时,进入whlie循环:



因为此时的cur为null了,所以得从c步骤重新开始再走一遍.s不为null.

public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list=new ArrayList<>();Stack<TreeNode> s=new Stack<>();TreeNode cur=root;s.push(cur);while(!s.empty()){cur=s.pop();while(cur!=null){list.add(cur.val);if(cur.right!=null){s.push(cur.right);}cur=cur.left;}}return list;
}

中序遍历

public List<Integer> inorderTraversal(TreeNode root) {List<Integer> list=new ArrayList<>();if(root==null){//说明是空树，直接返回一个空的list就行。return list;}TreeNode cur=root;Stack<TreeNode> s=new Stack<>();while(!s.empty()||cur!=null){while(cur!=null){s.push(cur);cur=cur.left;}cur=s.pop();list.add(cur.val);cur=cur.right;}return list;
}

后序遍历

public List<Integer> postorderTraversal(TreeNode root) {List<Integer> list=new ArrayList<>();if(root==null){return list;}TreeNode cur=root;TreeNode prev=null;Stack<TreeNode> s=new Stack<>();while(!s.empty()||cur!=null){while(cur!=null){s.push(cur);cur=cur.left;}TreeNode top=s.peek();if(top.right==null || top.right==prev){list.add(top.val);prev=top;s.pop();}else{cur=top.right;}}return list;}

c. 层次遍历

从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左往右访问第二层的节点,接着是第三层,以此类推,自上而下,自作向右逐层访问树的节点的过程就是层序遍历.

比如上图经过层次遍历的结果就是:1--->2--->4--->3--->5--->6.

2.4.3 还原二叉树

a.通过前序和中序的结果还原二叉树

还原思想:

前序: 根 左子树 右子树—通过前序遍历结果可以找到二叉树或者其子树的根节点
中序: 右子树 根 左子树—在中序结果中找到根的位置,根左边的是左子树的节点,右边是右子树的节点.

来看个例题:

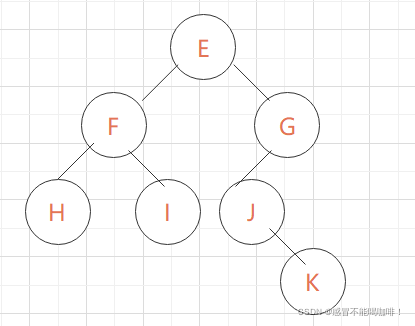
前序遍历结果: EFHIGJK,中序遍历结果: HFIEJKG,请还原二叉树

题解:

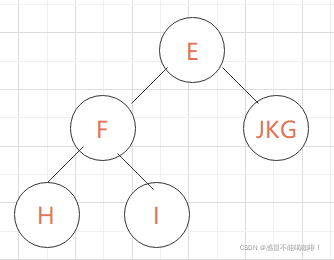
我们通过前序遍历的结果可以得出二叉树的根节点为E,通过中序遍历结果可知HFI是根的左子树,JKG是根的右子树.

再通过前序遍历可知左子树的根节点为F,所以H是F的左节点,I是F的右节点.

从前序结果当中可知,G是右子树的根节点,J是G的左子树,然后从中序遍历可知,K是J的右子树.
最后还原后的图形为:

b.通过中序和后序的结果还原二叉树

还原思想:

后序: 左子树 右子树 根----在后序结果中确定二叉树的根节点.
中序: 右子树 根 左子树----在中序结果中找到根的位置,根左边的是左子树的节点,右边是右子树的节点.

来看个例题:

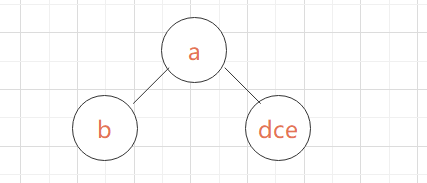
中序遍历结果为:badce,后序遍历结果为:bdeca

题解:

先从后序遍历结果中确定二叉树的根节点为a,再从中序结果中得知a的左子树是b,a的右子树是dce

从后序结果可知c是右子树的根节点.从中序结果可知,d是c的左子树,e是c的右子树.

注意:通过前序遍历结果和后序遍历结果不能还原出二叉树.
前序:根 左子树 右子树
后序:左子树 右子树 根
只能找到根节点,不能确定根节点的左右子树.

c.通过层次遍历的结果还原二叉树.

这个相对来说就很简单了,自上而下,自左向右进行还原就行.
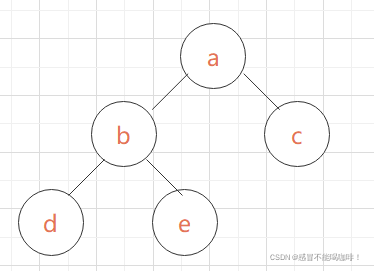
比如层次遍历结果是abcde,还原二叉树.
我们直接给出图形就行:

2.4.4 二叉树的基本操作方法

方法名	作用
int size(Node root)	获取树中节点的个数
int getLeafNodeCount(Node root)	获取叶子节点的个数
int getLevelNodeCount(Node root)	获取第k层节点的个数
int getHeight(Node root)	获取二叉树的高度
Node find(Node root,int value)	检测值为value的元素是否存在
boolean is CompleteTree(Node root)	判断一棵树是不是完全二叉树