数据结构与算法之树

数据结构与算法之树（一）二叉树概念及遍历方式（图文并茂）

数据结构与算法之树（二）二叉查找树

数据结构与算法之树（三）AVL树

数据结构与算法之树（四）红黑树

数据结构与算法之树（二）二叉查找树

文章目录

数据结构与算法之树（二）二叉查找树
- 一、二叉查找树结构
- 二、二叉查找树查找
- 三、二叉查找树插入
- 四、二叉查找树删除
- 五、二叉查找树的不足

一、二叉查找树结构

二叉查找树的二叉树的一种常见类型，又可以称为二叉搜索树。顾名思义，二叉查找树支持快速的查找，不仅如此，它还支持快速的插入与删除，二叉查找树是如何实现这些特性的呢？

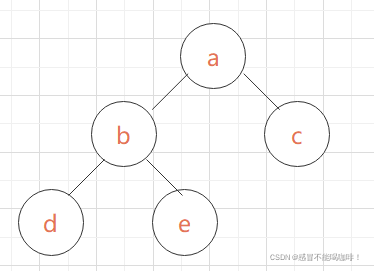
这就需要看二叉查找树的结构，二叉查找树要求任意一个节点，其左子树的每个节点的值要小于此节点，右子树中每个节点的值要大于此节点，如下图就是一棵二叉查找树

在这里插入图片描述

可以看到，每一个节点的左子树的节点的值都小于该节点，右子树的节点的值都大于该节点

了解了二叉查找树的结构后，关于二叉查找树如何查找、插入、删除下面将一一讨论

二、二叉查找树查找

二叉搜索树的查找是采用二分的思想

查找方法如下

首先从根节点开始，如果要查找的值等于该节点的值，那么就返回。否则，如果要查找的值小于该节点的值，那么就往左节点跳，如果要查找的值大于该节点的值，那么就往右节点跳

下面以我们在以下这棵二叉查找树中，来查找5这个值

在这里插入图片描述

查找步骤

①我们从根节点开始查找

②5比7小，那么往左节点跳

③5比4大，往右节点跳

④5比6小，往左节点跳，此时找到值等于5的节点，查找成功返回

在这里插入图片描述

查找的程序如下

#include <stdio.h>
#include <stdlib.h>struct Node
{int value;Node* left;Node* right;
};struct Node* root;struct Node* binarySearchTreeFind(struct Node** root, int value)
{struct Node* node = *root;while(node != NULL){if(value < node->value)node = node->left;else if(value > node->value)node = node->right;elsereturn node;}return NULL;
}

三、二叉查找树插入

二叉查找树的插入和查找做法十分类似，都是采用二分的思想

插入方法如下

首先从根节点开始，如果插入的值小于该节点的值，那么就往左跳，否则就往右跳，直到找到空位置，这里就是插入节点

下面考虑在这棵二叉搜索树中，插入2这个数的整一个过程

在这里插入图片描述

插入步骤

①从根节点开始

②发现2比7小，那么往左节点跳

③2比4小，继续往左节点跳

④2比1大，此时发现1的右孩子为空，那么就找到了插入位置，在此处插入值为2的节点

在这里插入图片描述

你可能会发现，我们并没有将等于作为一种特殊情况，而是将其归为大于等于，这是因为我们允许插入值相同的节点，继续上面的二叉搜索树为例，如果插入4这个已存在的值，最后会插入到哪里

在这里插入图片描述

插入的程序如下

struct Node* createNode(int value)
{struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));newNode->value = value;newNode->left = NULL;newNode->right = NULL;return newNode;
}void binarySearchTreeInsert(struct Node** root, int value)
{struct Node* node = *root;/* 树根为空，为其创建一个节点 */if(node == NULL){*root = createNode(value);return;}struct Node* pNode; //保留父节点while(node != NULL){pNode = node;if(value < node->value)node = node->left;elsenode = node->right;}/* 插入新节点 */if(value < pNode->value)pNode->left = createNode(value);elsepNode->right = createNode(value);
}

四、二叉查找树删除

相对于查找和插入，删除就显得复杂一点了

删除方法

总的可以分为下面三种情况

1.如果删除节点没有左右子节点，我们只要将其父节点指向该节点的指针设置为空，然后删除该节点接口

2.如果删除节点有一个子节点，那么我们将其父节点指向删除节点的指针指向删除节点的子节点，然后删除该节点

3.如果删除节点有左右两个子节点，这种情况稍微复杂，我们需要将其右子树最左的节点来替换该节点，然后删除该节点

对于上面这几种情况可能会稍微复杂，下面我使用图示你就明白了

首先有请我们要操作的二叉查找树出场

在这里插入图片描述

情况1

删除节点没有子节点

我们以值为9的这个节点为例，将其删除，如下

在这里插入图片描述

情况2

删除节点有一个子节点

我们以值为5的这个节点为例，将其删除，如下

在这里插入图片描述

情况3

删除节点有左右两个子节点

这种情况是比较复杂的，首先需要找到删除节点右子树最左的节点，将其替换删除节点，如下

我们以值为3的这个节点为例，将其删除，如下

在这里插入图片描述

为什么需要找到右子树的最左节点呢？

我们想一下，在删除3节点的时候，肯定需要找一个新节点来替代它，那么此时是1或者6节点，那么就会破坏二叉查找树的规则

我们需要找的是，大于删除节点的左子树，小于删除节点的右子树，为了大于删除节点的左子树，那么就需要在删除节点的右子树查找，为了小于删除节点的右子树，那么就必须是删除节点右子树最左边的节点

删除指定节点的程序如下

void binarySearchTreeDelete(struct Node** root, int value)
{struct Node* node = *root;struct Node* pNode = NULL; //保存父节点struct Node* curNode = NULL;/* 查找要删除的节点 */while(node != NULL){if(value < node->value){pNode = node;node = node->left;}else if(value < node->value){pNode = node;node = node->right;}elsebreak;}/* 没有找到 */if(node == NULL)return;if(node->left == NULL && node->right == NULL) //case 1{if(pNode)  //删除节点不是根节点value < pNode->value ? pNode->left = NULL : pNode->right = NULL;else //删除节点为根节点curNode = NULL;free(node);}else if(node->left != NULL && node->right != NULL) //case 3{struct Node* minNode = node->right; //右子树最左节点struct Node* pMinNode = node; //右子树最左节点的父节点while(minNode->left != NULL){pMinNode = minNode;minNode = minNode->left;}/* 替换要删除的节点 */node->value = minNode->value;if(pMinNode == node) //右子树没有左节点pMinNode->right = minNode->right;else //找到了右子树的最左节点pMinNode->left = NULL;free(minNode);/* 如果删除的是根节点 */if(!pNode)curNode = node;}else //case 2{if(node->left != NULL) //左子节点不为空{if(pNode) //删除节点不是根节点value < pNode->value ? pNode->left = node->left : pNode->right = node->left;else //删除节点为根节点curNode = node->left;free(node);}else //右子节点不为空{if(pNode) //删除节点不是根节点value < pNode->value ? pNode->left = node->right : pNode->right = node->right;else //删除节点为根节点curNode = node->right;free(node);}}/* 如果删除的是根节点 */if(!pNode)*root = curNode;
}

可以看到删除的代码还是比较复杂的

你可以将上面的几段代码拷贝下来，运行下面的测试程序

int main(int argc, char* argv[])
{struct Node* node;int value;int i;for(i = 0; i < 50000; ++i){value = rand() % 50000;binarySearchTreeInsert(&root, value);}for(i = 50; i < 70; ++i){node = binarySearchTreeFind(&root, i);if(node)printf("find %d\n", node->value);}for(i = 10000; i < 10020; ++i){node = binarySearchTreeFind(&root, i);if(node)printf("find %d\n", node->value);}for(i = 500; i < 550; ++i)binarySearchTreeDelete(&root, i);return 0;
}