树一：邂逅入门篇

article/2025/8/19 6:29:53

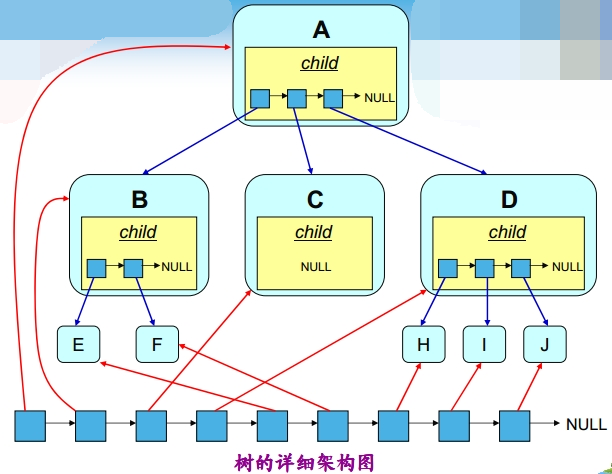
一、树的概念

树是一种典型的非线性结构，是表达有层次特性的图结构的一种方法。

1.1 基本术语

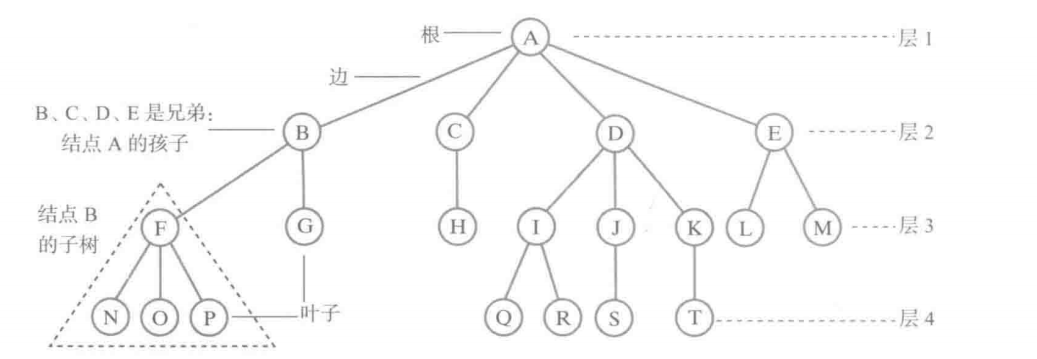
在这里插入图片描述

术语描述
空树当n=0 时称为空树。
根结点根结点是一个没有双亲结点的结点。一棵树最多一个。例如：A
边结点之间的连线
叶子结点没有孩子结点的结点。例如：N、O、P
兄弟结点同一双亲的孩子结点； 堂兄结点：同一层上结点
祖先结点从根到该结点的所经分支上的所有结点
子孙结点以某结点为根的子树中任一结点都称为该结点的子孙
结点层根结点的层定义为1；根的孩子为第二层结点，依此类推；
树的深度树中最大的结点层
树的高度跟树的深度一个意思。树中所有结点高度的最大值
结点的度结点子树的个数
树的度树中最大的结点度。
分枝结点度不为0的结点；
有序树子树有序的树，如：家族树；
无序树不考虑子树的顺序

注意：有写书定义书高和层是从0开始的。如：根结点在0层

  • 树的度
    https://xiaozhuanlan.com/topic/7189032546
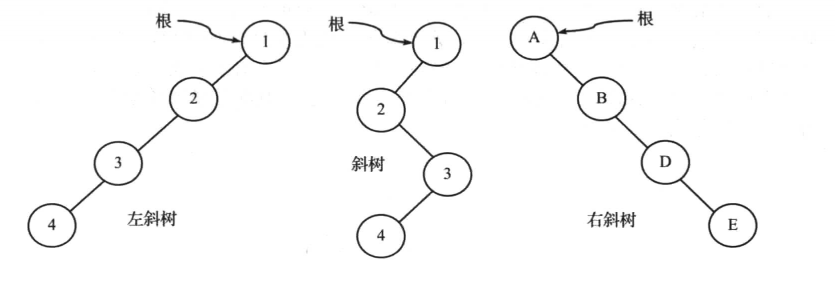
  • 如果树除了叶子结点外，其余每一个结点只有一个孩子结点，则这种树称为斜树； 所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。

在这里插入图片描述

1.2 二叉树

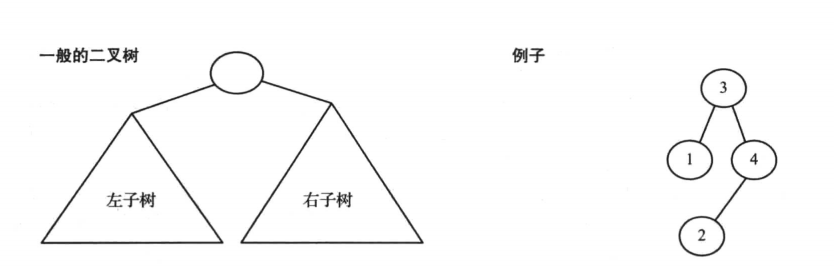
如果一棵树的每个结点有0 、1 后者 2个结点（最多两个孩子结点），那么这棵树称为二叉树。空树也是一棵有效的二叉树。二叉树的子树还是二叉树。实际上可以递归定义二叉树。(因为这个特性，对二叉树的操作常常使用递归算法)
在这里插入图片描述

  • 满二叉树/满树： 二叉树中的每个结点恰好有两个孩子结点且所有叶子结点都在同一层。

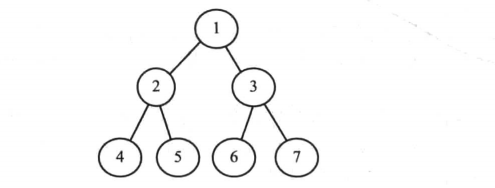
在这里插入图片描述

  • 完全二叉树/完全树：对一颗具有n个结点的二叉树按层编号，如果编号为i(1<=i<=n) 的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树

倒数第二层是满的，且最后一层的叶子结点从左至右填充

在这里插入图片描述

  • 平衡二叉树： 如果树中的每个结点的子树的高度差不大于1，则树称为高度平衡的或者平衡的。

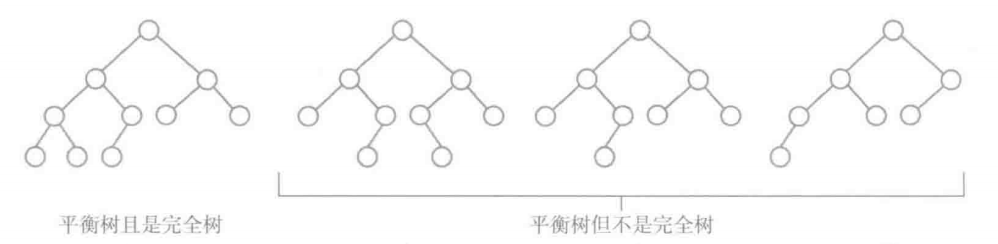
在这里插入图片描述

  • 完全平衡树： 若二叉树中的每个结点有两棵高度相等的子树，则该树称为完全平衡树。唯一的完全平衡二叉树是满树。
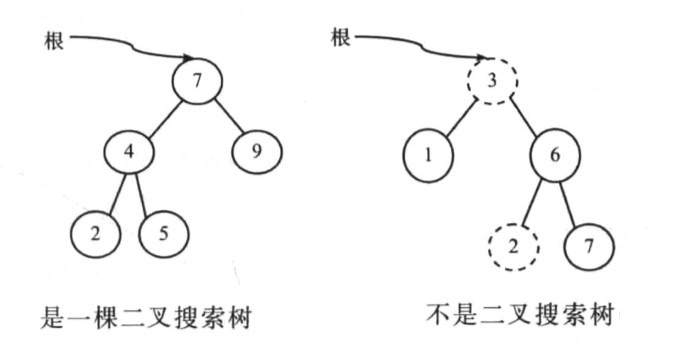
  • 二叉搜索树

二叉查找树是一棵二叉树、其结点含有comparable类型的对象，并遵循以下规则：

  1. 结点中的数据大于结点左子树中的所有数据。
  2. 结点中的数据小于结点的右子树中的所有数据。
  3. 左子树和右子树也都必须是二叉查找树
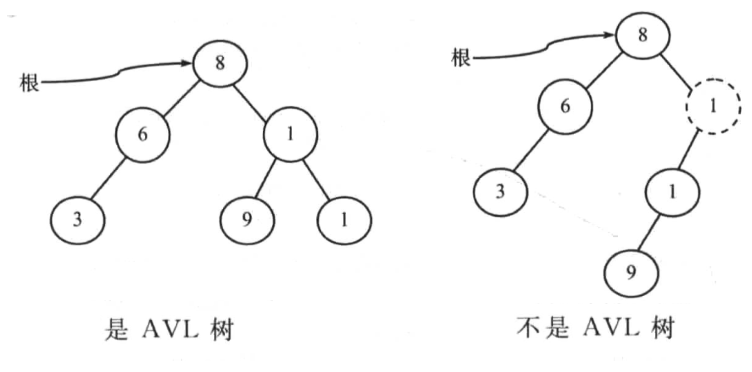
    在这里插入图片描述
  • 平衡二叉查找树(AVL 树)

是平衡树和二叉搜索树的结合

在HB(k)中，如果k=1，那么这样的二叉搜索叫做AVL树。即一棵AVL树是带有平衡条件的二叉搜索树。 左子树和右子树的高度最多不能超过1

在这里插入图片描述

  • 红黑色
    在红黑树中，每个结点关联一个额外的属性：红色或者黑色中的一种颜色。
    定义：红黑树是一棵满足以下性质的二叉搜索树：
  1. 根结点是黑色
  2. 每个叶子结点是黑色
  3. 红色结点的孩子结点是黑色

1.3 满树(满二叉树)或完全树(完全二叉树)的高度

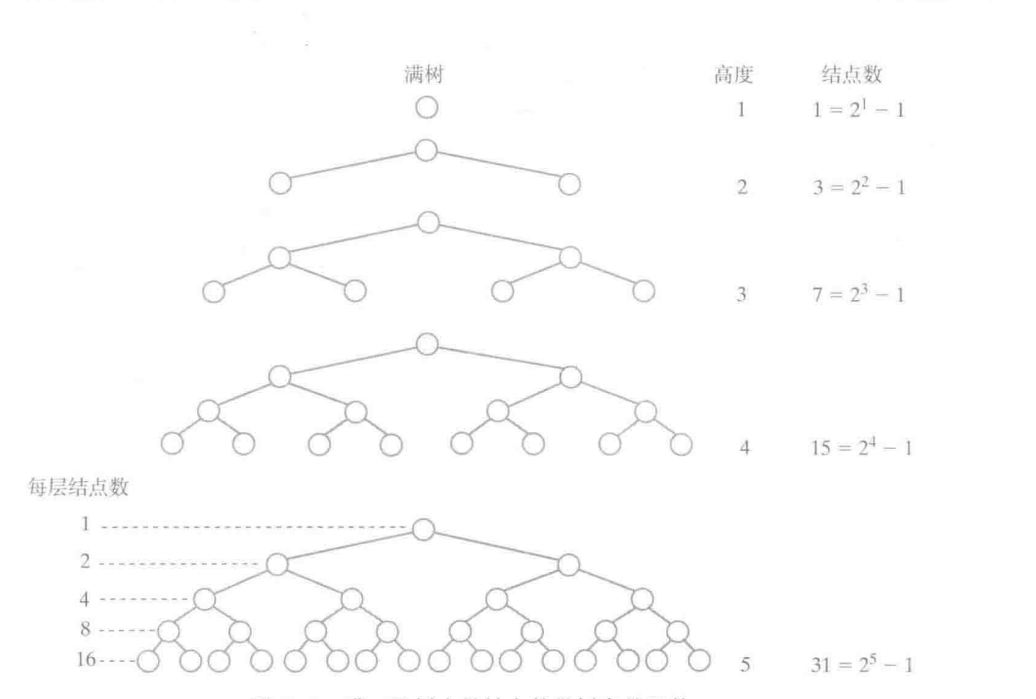在这里插入图片描述其中h是树的高度，如果满树的结点树为n，则有

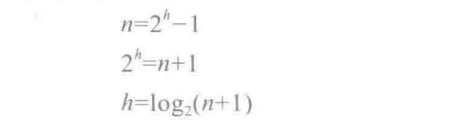
在这里插入图片描述

即含有n个结点的满树的高度是 log2(n+1)。含n个结点的完全树的高度是对 log2(n+1)向上取整。

含有n个结点的完全二叉树或满二叉树的高度是对log2(n+1)向上取整

1.4 其他、 二叉树的应用

  • 编译器中的表达式
  • 用于数据压缩算法中哈弗曼编码树
  • 二叉搜索树(查找树)BST
  • 优先队列(PQ)
    ……

1.5 二叉树的结构

在这里插入图片描述

为了简单起见，数据设定为整数

//java语言描述
public class BinaryTreeNode {private int data;private BinaryTreeNode leftTree;private BinaryTreeNode rightTree;……
}

1.6 二叉树的操作

  • 基本操作
    • 插入
    • 删除
    • 查找
    • 遍历
  • 辅助操作
    • 树大小
    • 树高
    • 树最大层
    • 给定两个或多个节点，找最近公共祖先

……

二 、树的遍历

2.1 二叉树的遍历

为了对树结构进行处理，需要一种机制来遍历树中的结点。在遍历过程中，每个结点只能被处理一次，但可以被访问多次。

  • 前序遍历/先序遍历：
    在访问根的子树之前访问根。然后访问根的左子树中所有的结点，再访问根的右子树中的所有结点。
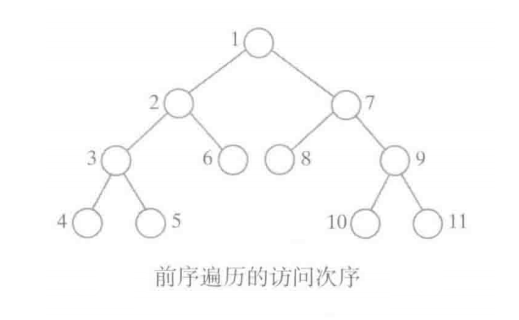
    在这里插入图片描述

递归方式

 public static void preOrder(BinaryTreeNode root) {if(null != root) {System.out.print(root.getData() + " ");preOrder(root.getLeftTree());preOrder(root.getRightTree());}}

非递归方式

为了模拟递归：首先处理当前结点，在遍历左子树之前，把当前结点保留到栈中，当遍历完左子树后，将该元素出栈，然后找打其右子树进行遍历。直到栈为空为止。

    public static void preOrderNonRecursive(BinaryTreeNode root) {if(null == root) {return;}Stack<BinaryTreeNode> s = new Stack<BinaryTreeNode>(); // FILOwhile (true) {while (null != root) {System.out.print(root.getData() + " ");s.push(root);root = root.getLeftTree();}if(s.isEmpty()) {break;}root = s.pop();root = root.getRightTree();}}
  • 中序遍历：
    在中序遍历中，根结点的访问在两棵子树的遍历中间完成。
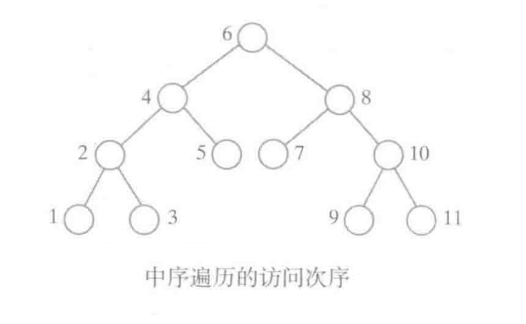
    在这里插入图片描述

递归方式：

public static void inOrder(BinaryTreeNode root) {if(null != root) {inOrder(root.getLeftTree());System.out.print(root.getData() + " ");inOrder(root.getRightTree());}
}

非递归方式：

非递归中序遍历类似前序遍历。唯一区别是，首先要移动到结点的左子树，完成左子树的遍历后，再将结点出栈进行处理。

   public static void inOrderNonRecursive(BinaryTreeNode root) {if(null == root) return;Stack<BinaryTreeNode> stack = new Stack<BinaryTreeNode>();while (true) {while (null != root) {stack.push(root);root = root.getLeftTree();}if(stack.isEmpty()) return;BinaryTreeNode node = stack.pop();System.out.print(node.getData() + " ");root = node.getRightTree();}}
  • 后序遍历：
    访问二叉树的根的子树中的结点之后访问树的根
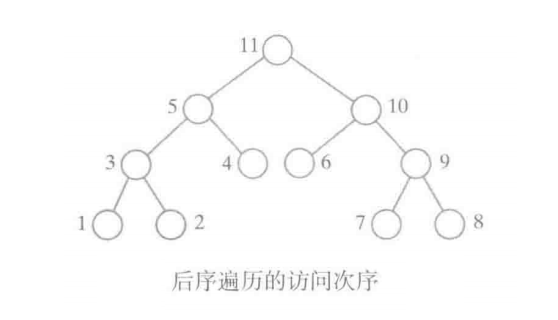
    在这里插入图片描述

递归方式：

    public static void postorder(BinaryTreeNode root) {if(null != root) {postorder(root.getLeftTree());postorder(root.getRightTree());System.out.print(root.getData() + " ");}}

非递归方式：

①：前序、中序遍历中，当元素出栈后就不需要再次访问该结点了，但是后序遍历中，每个结点需要访问两次。
②：当从栈中出栈一个元素时，检查这个元素与栈顶元素的右子树是否相同。如果相同，则说明已经完成了左、右子树的遍历。此时，只需要再将栈顶元素出栈一次病输出该结点数据即可。

    public static void postOrderNonRecursive(BinaryTreeNode root) {if(null == root) return;Stack<BinaryTreeNode> stack = new Stack<>();while (true) {if (null != root) {stack.push(root);root = root.getLeftTree();} else {if(stack.isEmpty()) {return;}else {if(null == stack.peek().getRightTree()) {root = stack.pop();System.out.print(root.getData() + " ");if(!stack.isEmpty() && root == stack.peek().getRightTree()) {//左右子树遍历完成System.out.println(stack.peek().getData() + " ");stack.pop();if(stack.isEmpty()) {break;}}root = null;} else {//exists the right subtreeroot = stack.peek().getRightTree();stack.peek().setRightTree(null);}}}}}
  • 层序遍历：
    从根开始，每次访问一层中的结点。在同一层中，从左至右访问。
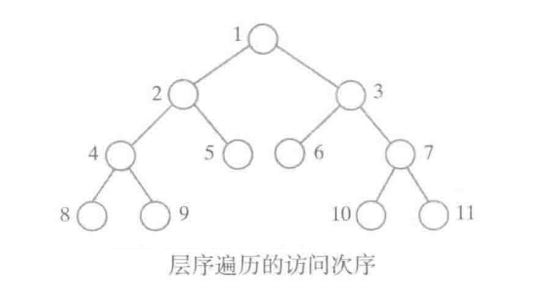
    在这里插入图片描述

层序遍历需要借助队列来完成

   public static void levelOrder(BinaryTreeNode root) {if(null == root) return;Queue<BinaryTreeNode> queue = new ArrayDeque<>();queue.add(root);BinaryTreeNode temp = null;while (!queue.isEmpty()) {temp = queue.poll();//处理当前结点System.out.print(temp.getData() + " ");if(null != temp.getLeftTree()) {queue.add(temp.getLeftTree());}if(null != temp.getRightTree()) {queue.add(temp.getRightTree());}}}

广度优先遍历：层序遍历是广度优先遍历的示例
深度优先遍历：前序遍历是深度优先遍历的示例

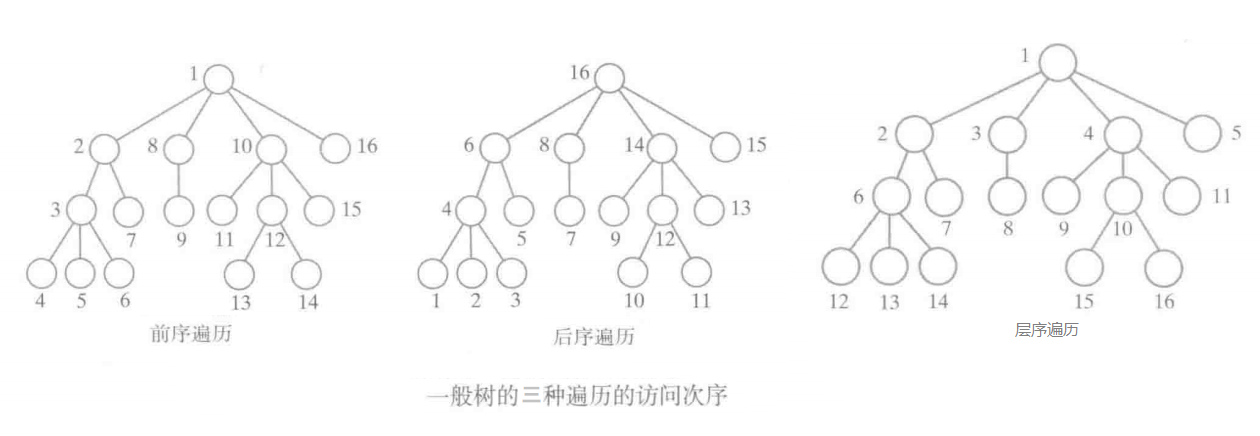
2.2一般树的遍历

一般树的遍历有层序、前序和后序、对一般树而言，中序遍历不好定义。

在这里插入图片描述

三、树的示例

一些使用树来组织数据的示例。

3.1 表达式树

可以用二叉树来表示其运算符为二元运算符的代数表达式。孩子的次序要与操作树的次序想匹配。这样的二叉树称为表达式树。

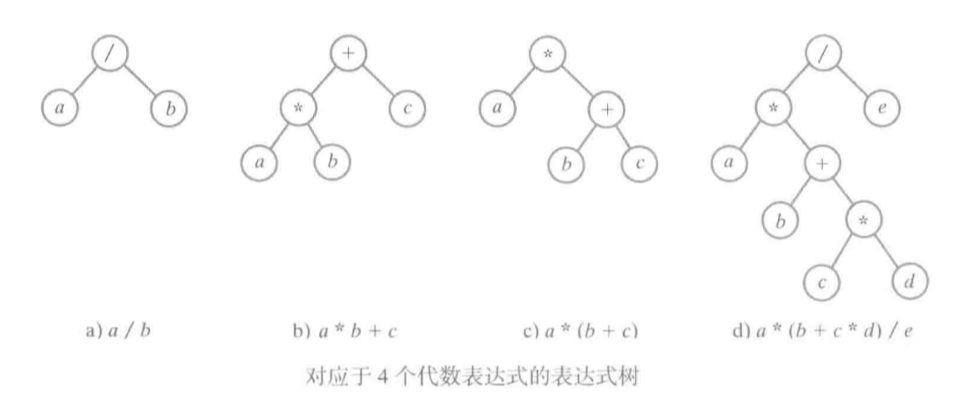**加粗样式**事实上，不需要括号，树也能得到表示中的运算符的次序。代数表达式有不同的写法。正常书写的表达式，即每个二元运算符出现在两个操作数的中间，称为中缀表达式。前缀表达式将每个运算符都放在其两个操作的前面，后缀表达式将每个运算符都放在其两个操作数的后面。

3.2 二叉查找树 / 二叉搜索树

二叉查找树是一棵二叉树、其结点含有comparable类型的对象，并遵循以下规则：

  • 结点中的数据大于结点左子树中的所有数据。
  • 结点中的数据小于结点的右子树中的所有数据。
  • 左子树和右子树也都必须是二叉查找树
    在这里插入图片描述

例如：字符串二叉查找树、Jared大于Jared的左子树中的所有名字，但小于Jared的右子树中的所有名字。

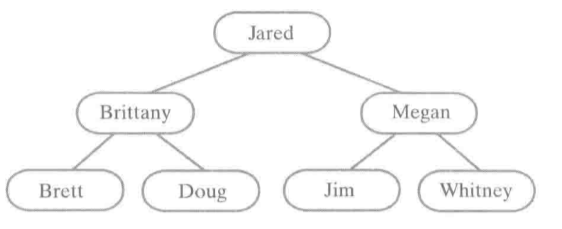
在这里插入图片描述

下面是也是一棵二叉查找树

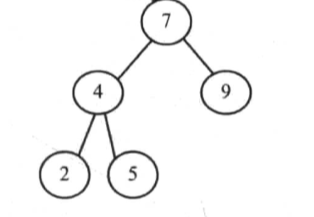
在这里插入图片描述
注意： 上面二叉查找树的定义，隐含表明树中的所有项都是不同的。但允许树中有重复的值

二叉查找树的形态是不唯一的。即对同样的一组数据，可以组成几棵不同的二叉查找树。例如：

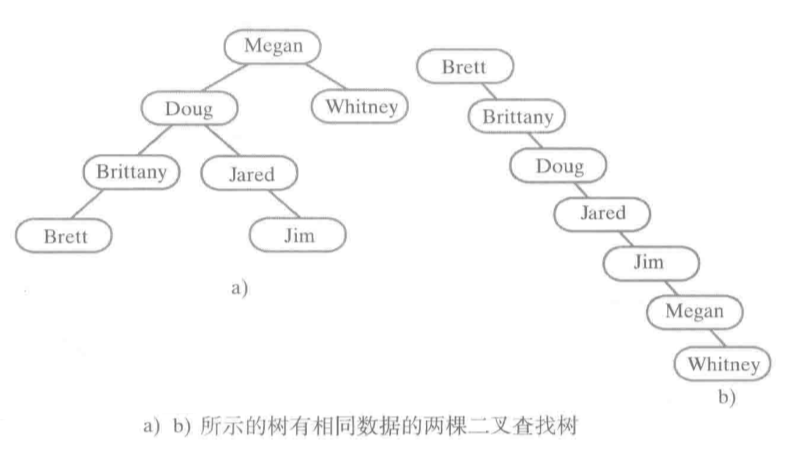
在这里插入图片描述

3.3 堆

堆(heap) 是其结点含有 Comparable对象的一棵完全二叉树，且满足以下条件：每个结点的对象不小于(或不大于)其后代的对象。 在最大堆中，结点中的对象大于或等于其后代的对象。 在最小堆中，关系是小于或等于。
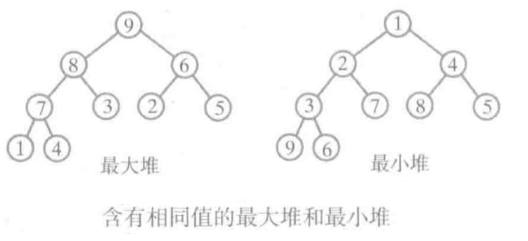在这里插入图片描述最大/小堆的任何结点的子树仍然是最大/小堆。

可以用堆实现优先队列

小结

本篇是对树的一个入门，讲解了树的一些基本概念、并对二叉树的三种遍历做了全面的介绍，给出了java描述。后面讲解了一些其他平衡树的知识，也给出了一些树的示例。

参考

  • 《数据结构与算法经典问题解析-Java语言描述》
  • 《数据结构与抽象Java语言描述第4版》
  • 参考 【https://xiaozhuanlan.com/topic/7189032546】

http://chatgpt.dhexx.cn/article/WVCjWDYj.shtml

相关文章

树一：定义及存储

树一：定义及存储

树的定义&#xff1a; 树是一种非线性的数据结构。树是由 n (n > 0) 个结点组成的有序集合。 如果 n 为0&#xff0c;称为空树&#xff1b;如果 n > 0, 则&#xff1a; 有一个结点称为根结点&#xff08;root&#xff09;&#xff0c;它有直接后继&#xff0c;但没有直接…
阅读更多...
mysql 创建索引规则

mysql 创建索引规则

1、表的主键、外键必须有索引&#xff1b; 2、数据量超过300的表应该有索引&#xff1b; 3、经常与其他表进行连接的表&#xff0c;在连接字段上应该建立索引&#xff1b; 4、经常出现在Where子句中的字段&#xff0c;特别是大表的字段&#xff0c;应该建立索引&#xff1b; 5、…
阅读更多...
mysql分区表之三：MySQL分区建索引,唯一索引

mysql分区表之三：MySQL分区建索引,唯一索引

介绍 mysql分区后每个分区成了独立的文件&#xff0c;虽然从逻辑上还是一张表其实已经分成了多张独立的表&#xff0c;从“information_schema.INNODB_SYS_TABLES”系统表可以看到每个分区都存在独立的TABLE_ID,由于Innodb数据和索引都是保存在".ibd"文件当中&#…
阅读更多...
分享mysql创建索引的3种方法

分享mysql创建索引的3种方法

大家应该都知道索引的建立对于MySQL数据库的高效运行是很重要的,索引可以大大提升MySQL的检索速度,下面这篇文章主要给大家介绍了关于mysql创建索引的3种方法,需要的朋友可以参考下 1、使用CREATE INDEX创建&#xff0c;语法如下&#xff1a; 1 CREATE INDEX indexName ON tab…
阅读更多...
js 监听浏览器刷新还是关闭事件

js 监听浏览器刷新还是关闭事件

// $(window).bind(beforeunload,function(){return 您输入的内容尚未保存&#xff0c;确定离开此页面吗&#xff1f;;}); // window.onbeforeunload function() { return "确定离开此页面吗&#xff1f;"; }; // function myFunction() {return "自定…
阅读更多...
浏览器刷新和页面手动为什么不一样？

浏览器刷新和页面手动为什么不一样？

Fiddler(2):AutoResponse修改返回结果_mb5fed6ec4336ce的技术博客_51CTO博客Fiddler(2):AutoResponse修改返回结果&#xff0c;前言怎么修改接口的返回数据呢步骤1.抓包&#xff0c;找到要拦截的请求&#xff0c;然后在AutoResponder中AddRule&#xff1a;2.在RuleEditor中的第…
阅读更多...
vue监听浏览器刷新和关闭事件，并在页面关闭/刷新前发送请求

vue监听浏览器刷新和关闭事件，并在页面关闭/刷新前发送请求

vue监听浏览器刷新和关闭事件&#xff0c;并在页面关闭/刷新前发送请求 1.需求背景&#xff1a;2.需求分析&#xff1a;3.实现方式&#xff1a;4.实现方式解析&#xff1a;1&#xff09;浏览器页面事件基础2&#xff09;在mounted监听beforeunload和unload事件 5.存在的问题/风…
阅读更多...
浏览器刷新和关闭时显示提示信息

浏览器刷新和关闭时显示提示信息

vue 刷新和关闭浏览器时显示提示信息 使用onbeforeunload事件 mounted() {window.onbeforeunload e > {e e || window.eventif (e) {e.returnValue 关闭提示}return 关闭提示}} }, beforeDestroy() {window.onbeforeunload null },如果是所有页面都需要页面销毁显示提…
阅读更多...
【Vue实用功能】Vue监听浏览器刷新和关闭事件

【Vue实用功能】Vue监听浏览器刷新和关闭事件

Vue监听浏览器刷新和关闭事件 在前端开发中&#xff0c;我们通常会遇到这样的需求&#xff0c;用户离开、刷新页面前&#xff0c;修改数据未进行保存操作&#xff0c;需要提示框提醒用户 效果实现 methods: {/** 在刷新和关闭之前询问 **/beforeRefreshClose() {let self t…
阅读更多...
vue监听浏览器刷新和关闭；

vue监听浏览器刷新和关闭；

注意&#xff1a;区分不了浏览器是触发了刷新还是关闭&#xff0c;而且提示的弹框是无法自定义的&#xff1b;如果有大佬有方法能区分&#xff0c;还请评论学习一下&#xff01;感谢&#xff01; 代码可直接复制&#xff1a; <template><div><div /></di…
阅读更多...
JS阻止浏览器刷新的方法

JS阻止浏览器刷新的方法

直接先给朋友们上阻止浏览器刷新的代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><meta http-equiv&quo…
阅读更多...
VSCODE同步浏览器刷新

VSCODE同步浏览器刷新

VSCODE同步浏览器刷新 安装插件 live server
阅读更多...
java中foreach的用法

java中foreach的用法

文章目录 前言语法用法用法1&#xff1a;输出一维数组用法2&#xff1a;输出二维数组foreach的局限性什么是索引 总结 前言 java中foreach,可以认为是增强版的for语句循环&#xff0c;它可以减少代码量&#xff0c;但是不是所有的foreach都可以代替for循环。 语法 foreach的…
阅读更多...
JAVA实现九九乘法表

JAVA实现九九乘法表

用java语言实现九九乘法表&#xff0c;这里使用的是for循环 public class NineNineDemo{public static void main(String[] args){int i1;//对行变量赋值int j1;//对列变量赋值for(i1;i<9;i){for(j1;j<i;j){//行变量外循环&#xff1b;列变量内循环System.out.print(i&q…
阅读更多...
Java的ASCII编码表

Java的ASCII编码表

数字和字符的对照关系表&#xff08;编码表&#xff09;&#xff1a; ASCII码表&#xff1a;American Standard Code for Information Interchange, 美国信息交换标准代码。 Unicode码表&#xff1a;万国码。也是数字和符号的对照关系&#xff0c;开头0-127部分和ASCII完全一样…
阅读更多...
JAVA——链表

JAVA——链表

一、链表概念及结构 链表&#xff1a;链表是一种物理存储结构上非连续存储结构&#xff0c;数据元素的逻辑顺序是通过链表中的引用链接次序实现的。如下图&#xff1a;&#xff08;通俗的说&#xff1a;就是由一个个节点组成&#xff0c;这些节点逻辑上连续&#xff0c;物理上…
阅读更多...
java对象复制_Java对象的复制三种方式

java对象复制_Java对象的复制三种方式

Java对象的复制三种方式 概述 在实际编程过程中，我们常常要遇到这种情况：有一个对象A，在某一时刻A中已经包含了一些有效值，此时可能 会需要一个和A完全相同新对象B，并且此后对B任何改动都不会影响到A中的值，也就是说，A与B是两个独立的对象，但B的初始值是由A对象确定的。…
阅读更多...
Java 如何复制 List ?

Java 如何复制 List ?

List 复制在项目开发时&#xff0c;使用到的频率还是比较高的。List 复制有浅拷贝和深拷贝两种方式。在陈述复制方法前&#xff0c;先总结下什么是浅拷贝和深拷贝(以下内容均站在 Java 语言基础上进行讨论)。 一、什么是浅拷贝&#xff08;Shallow Copy&#xff09;和深拷贝&a…
阅读更多...
Java对象复制

Java对象复制

文章目录 前言何不可变类对象复制方式1.直接赋值2.浅拷贝3.深拷贝 对象复制方案1.get/set2.Spring BeanUtils3.Apache BeanUtils4.BeanCopier5.Orika6.Dozer7.MapStruct8.Bean Mapping9.Bean Mapping ASM10.ModelMapper11.JMapper12.Json2Json 复制方案选择 前言 在我们实际项…
阅读更多...
Java 复制Excel工作表

Java 复制Excel工作表

本文归纳了关于Java如何复制Excel工作表的方法&#xff0c;按不同复制需求&#xff0c;可分为&#xff1a; 1. 复制工作表 1.1 在同一个工作簿内复制工作表 1.2 在不同工作簿间复制工作表 2. 复制指定单元格数据 对于复制方法copy()&#xff0c;这里简单整理了一个表格&am…
阅读更多...
推荐文章

Copyright @ 2022~2023