背景概述

随着网络的规模越来越庞大，网络中的设备种类繁多，如何对越来越复杂的网络进行有效的管理，从而提供高质量的网络服务已成为网络管理所面临的最大挑战。网络管理已成为整个网络解决方案中重要的一部分。

网络管理通常包含4个要素：

被管理节点：需要进行管理的设备。
代理（Agent）：跟踪被管理设备状态的软件或硬件。
网络管理工作站（Manager）：与在不同的被管理节点中的代理通信，并且显示这些代理状态的设备。
网络管理协议：网络管理工作站和代理用来交换信息的协议。目前TCP/IP网络中应用最为广泛的网络管理协议是简单网络管理协议SNMP（Simple Network Management Protocol）。

SNMP简介

SNMP(Simple Network Management Protocol) 是一套网络管理协议，虽然名字叫做简单网络管理协议，但实际上并不是字面上的意思，尤其是看到.1.3.6.1.2.1.1.1.0这样一串串诡异的数字时候，就会有点让人崩溃。利用SNMP，一个管理工作站可以远程管理所有支持这种协议的网络设备，包括监视网络状态、修改网络设备配置、接收网络事件警告等。

基于SNMP的网管结构概述

基于SNMP的网络管理体系结构中包含4个主要组成部分：

网络管理站NMS（Network Management Station）

NMS通常是一个独立的设备，运行网络管理应用程序。网络管理应用程序至少能够提供一个人机交互界面，网络管理员通过它完成绝大多数网络管理工作。
SNMP代理器（Agent）

Agent是驻留在被管理设备的一个软件模块，主要负责接收和处理来自NMS的请求报文，并形成响应报文，返回给NMS；在一些紧急情况下，它会主动发送trap报文，通知NMS。
SNMP协议

SNMP协议属于TCP/IP网络的应用层协议，用于在NMS和被管理设备间交互管理信息。
管理信息库MIB（Management Information Base）

MIB是一个被管理对象的集合，是NMS同Agent进行沟通的桥梁，可以使网管软件和设备进行标准对接。每一个Agent都维护这样一个MIB库，NMS可以对MIB库中对象的值进行读取或设置。

基于SNMP网络管理的示意图

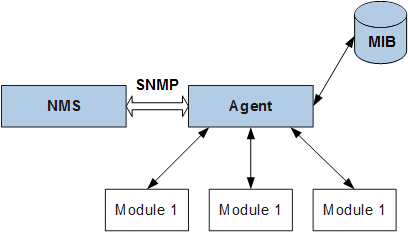
从图中可以了解网络管理中涉及到的几个主要组成部分的相互关系，它们之间的通信方式描述如下：

NMS通过SNMP协议与设备的Agent通信，完成对MIB的读取和修改操作，从而实现对网络设备的监控与管理。
SNMP是NMS与Agent之间通信的载体，通过其协议数据单元PDU（Protocol Data Unit）完成信息交换。SNMP并不负责数据的实际传输，数据交换的任务是通过UDP等传输层协议来完成的。
Agent是设备上的代理进程，主要工作包括与NMS通信，对设备中的MIB库进行维护，以管理和监控设备中的各个模块。
MIB保存设备中各个模块的信息。通过对MIB信息的读写操作来完成对设备的监控和维护。

SNMP协议

SNMP规定了5种协议数据单元PDU（也就是SNMP报文），用于NMS与Agent的交互。

各种报文的操作如下：

get-request：从代理进程处提取一个或多个参数值。
get-next-request：从代理进程处提取紧跟当前参数值的下一个参数值。
set-request：设置代理进程的一个或多个参数值。
get-response：返回的一个或多个参数值。这个操作是由代理进程发出的，它是对前面3种操作的响应。
trap：代理进程主动发出的报文，通知管理进程有某些事件发生。

前面3种操作由NMS向Agent发出，后面2种操作由Agent向NMS发出。

SNMP报文格式

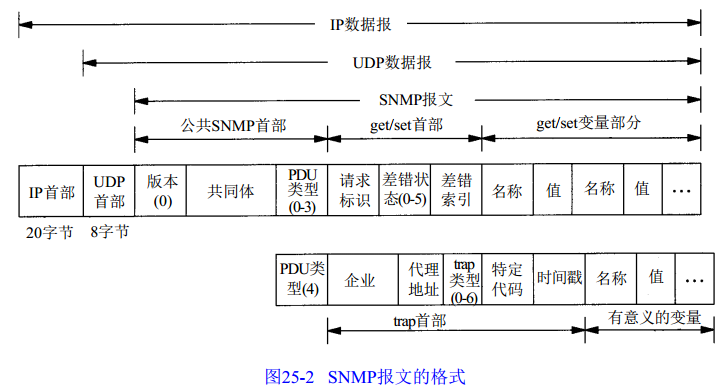
PDU类型的取值范围是0-4，正好表示5种SNMP消息。差错状态字段是一个整数，它是由代理进程标注的，指明有差错发生。

报文处理过程

Agent通过UDP端口161接收来自NMS的Request报文。

Agent接收到报文后，其基本处理过程如下：

解码：依据ASN.1基本编码规则，生成用内部数据结构表示的报文。如果此过程出现错误导致解码失败，则丢弃该报文，不做进一步处理。
比较SNMP版本号：将报文中的版本号取出，与本Agent支持的SNMP版本号比较。如果不一致，则丢弃该报文，不做进一步处理。
团体名验证：将报文中的团体名取出，此团体名由发出请求的网管站填写。如与Agent所在设备认可的团体名不符，则丢弃该报文，不做进一步处理，同时产生一个Trap报文。SNMPv1提供较弱的安全措施，在版本3中这一功能被加强。
提取PDU：从通过验证的ASN.1对象中提出协议数据单元PDU。如果失败，丢弃报文，不做进一步处理。
处理PDU：根据不同的PDU，SNMP协议实体进行不同的处理。得到管理变量在MIB树中对应的节点，从相应的模块中得到管理变量的值，形成Response报文，编码发回网管站。
网管站得到响应报文后，经过同样的处理，最终显示结果。

MIB

MIB（管理信息库）是一个被管理对象的集合，它定义被管理对象的一系列属性，包括

对象的名字
对象的访问权限
对象的数据类型

管理信息结构SMI（Structure of Management Information）规定了被管理的对象应该如何定义和组织，它定义了一系列MIB可以使用的数据类型，比如Counter、Gauge等。

MIB指明了网络元素所维护的变量，即能够被NMS查询和设置的信息，给出了一个网络中所有可能的被管理对象的集合的数据结构。

MIB树结构

MIB以树状结构进行存储，树的叶子节点表示管理对象，它可以通过从根节点开始的一条惟一路径来识别，这也就是OID（Object Identifier）。

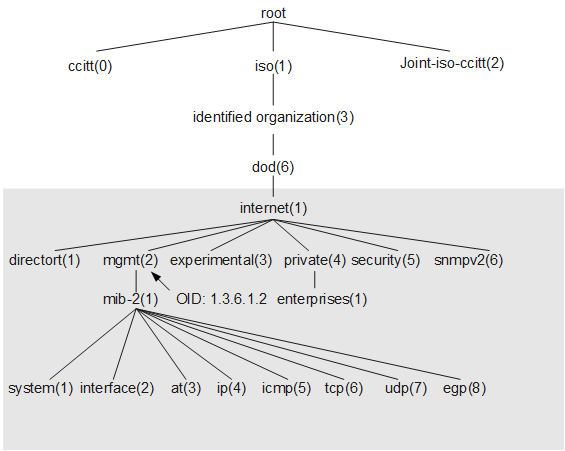
OID是由一些系列非负整数组成，中间以"."分割，用于唯一标识管理对象在MIB树中的位置。由SMI来保证OID不会冲突。在上图的树形结构中，mgmt对象可以标识为：1.3.6.1.2，这种标识就叫做OID。iso.org.dod.internet.private.enterprises（1.3.6.1.4.1）这个标识，是给厂家自定义而预留的，比如华为的为1.3.6.1.4.1.2011，华三的为1.3.6.1.4.1.25506。